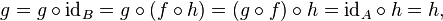Isomorphisme

Pour l'isomorphisme en chimie, voir Isomorphisme (chimie).

Pour l'isomorphisme institutionnel, voir Isomorphisme institutionnel.

En mathématiques, un isomorphisme entre deux ensembles structurés est une application bijective qui préserve la structure et dont la réciproque préserve aussi la structure^[1]. Plus généralement en théorie des catégories, un isomorphisme entre deux objets est un morphisme admettant un « morphisme inverse » .

D'autres termes peuvent être utilisés pour désigner un isomorphisme en spécifiant la structure, comme l'homéomorphisme entre espaces topologiques ou le difféomorphisme entre variétés.

Deux objets sont dits isomorphes s'il existe un isomorphisme de l'un vers l'autre. Dans certains contextes, un isomorphisme d'un objet sur lui-même est appelé un automorphisme.

Définitions

Algèbre

En algèbre, un isomorphisme est un morphisme admettant un inverse qui est lui-même un morphisme.

C'est donc une bijection pour laquelle les relations « algébriques » entre les éléments de l'ensemble d'arrivée sont les mêmes que celles entre leurs antécédents respectifs (la structure algébrique est préservée). Ce « méta-concept » mathématique admet une définition formelle en théorie des catégories.

Catégorie

Dans une catégorie donnée, un isomorphisme est un morphisme 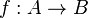$f:A\to B$ tel qu'il existe un morphisme 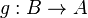$g:B\to A$ qui soit « inverse » de 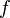$f$ à la fois à gauche 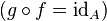$(g\circ f=\mathrm{id}_A)$ et à droite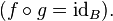 $(f\circ g=\mathrm{id}_B).$

Il suffit pour cela que f possède d'une part un « inverse à gauche » 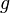$g$ et d'autre part un « inverse à droite » 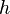$h$ . En effet, on a alors

g=g\circ\mathrm{id}_B=g\circ(f\circ h)=(g\circ f)\circ h=\mathrm{id}_A\circ h=h,

ce qui prouve en outre l'unicité de l'inverse.

En revanche, l'une ou l'autre de ces deux conditions, à elle seule, ne suffit pas.

Exemples

Dans la catégorie des ensembles, les isomorphismes sont les bijections.
Dans la catégorie des groupes, les isomorphismes sont les morphismes de groupes bijectifs.
Dans la catégorie des espaces topologiques, un isomorphisme est une bijection continue dont l'inverse est continue, aussi appelée homéomorphisme.
De la même façon, un isomorphisme entre variétés différentielles (par exemple, entre des ouverts de ℝⁿ) est un difféomorphisme, c'est-à-dire une bijection différentiable dont l'inverse est différentiable. Plus précisément, si l'on considère une structure C^k sur une variété, alors on parle de C^k-difféomorphisme.
Un isomorphisme d'ensembles ordonnés est une bijection croissante dont la réciproque est croissante.

Propriétés

Un isomorphisme est à la fois un épimorphisme et un monomorphisme, mais la réciproque est fausse en général : il existe des morphismes à la fois épiques et moniques qui ne sont pas des isomorphismes.

Pour plus de détails, voir : Propriétés des morphismes dans les catégories.

Objets isomorphes

Deux objets reliés par un isomorphisme sont dits isomorphes.

Exemple : le groupe de Klein est isomorphe à ℤ/2ℤ × ℤ/2ℤ.

Savoir que deux objets sont isomorphes présente un grand intérêt car cela permet de transposer des résultats et propriétés démontrés de l'un à l'autre.

Selon certains points de vue, deux objets isomorphes peuvent être considérés comme identiques, ou du moins indiscernables. En effet, bien souvent, les propriétés intéressantes d'un objet seront partagées par tous les objets isomorphes de la catégorie. Ainsi on parle souvent d'unicité ou d'identité « à isomorphisme près ».

Note

↑ Si, pour beaucoup de structures en algèbre, cette seconde condition est automatiquement remplie, ce n'est pas le cas en topologie par exemple où une bijection peut être continue sans que sa réciproque le soit.

Articles connexes

Théorèmes d'isomorphisme
Isomorphisme de graphes
Quasi-isomorphisme

Portail des mathématiques

This article is issued from Wikipédia - version of the Thursday, December 11, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.