Maillage

Pour les articles homonymes, voir Maillage (structure de données) et Mesh (objet).

Maillage d'un disque par des triangles (triangulation).

Un maillage est la discrétisation spatiale d’un milieu continu, ou aussi, une modélisation géométrique d’un domaine par des éléments proportionnés finis et bien définis. L'objet d'un maillage est de procéder à une simplification d'un système par un modèle représentant ce système et, éventuellement, son environnement (le milieu), dans l'optique de simulations de calculs ou de représentations graphiques.

On parle également dans le langage commun de pavage.

Définition et caractérisation d'un maillage

Principaux types d'éléments utilisé en 2D.

Principaux types d'éléments utilisé en 3D.

Un maillage est défini par :

• son repère ;
• les points le constituant, caractérisés par leurs coordonnées ;
• les cellules, constituant des polytopes reliant n de ces points ;

et peut être caractérisé notamment par :

• sa dimension : typiquement 2D ou 3D ;
• son volume (dimension totale couverte) ;
• sa finesse : surface ou volume moyen des cellules composant le maillage ;
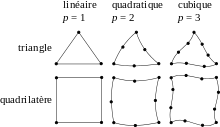
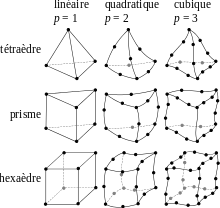
• la géométrie des cellules : triangles, quadrilatères (parallélogrammes, rectangles, carrés), …, polygones, en 2D ; tétraèdres, prismes, hexaèdres (parallélépipèdes, cubes), …, polyèdres en 3D ;
• le degré de l'élément : c'est le degré du polynôme servant à décrire les côtés ou arêtes des éléments, un élément de degré 1 a des côtés ou arêtes rectilignes ; dans le cas des éléments finis, c'est également le degré des polynômes d'interpolation

Les cellules ci-dessus ont des côtés rectilignes ou des faces planes, elles sont dites « linéaires » (définies par des lignes). On peut aussi utiliser des cellules dites « quadratiques » dont les lignes sont courbes. Chaque côté ou arête est alors défini par trois points : ses extrémités et son point milieu. Les cellules quadratiques permettent de décrire plus fidèlement la frontière de l'objet (on fait l'approximation d'une courbe par une parabole au lieu d'une corde), mais on augmente le nombre de points nécessaires pour décrire une cellule.

Maillage tétraédrique.

Maillage hexaédrique structuré.

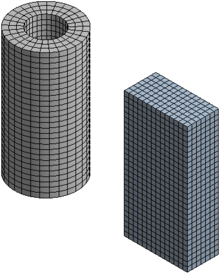
Les maillages les plus « efficaces » sont les maillages dits « réguliers » ou « structurés » : ils sont constitués de parallélogrammes en 2D, et de parallélépipèdes en 3D. Efficace signifie que ces maillages permettent d'économiser les ressources informatiques (mémoire, temps de calcul) :

• dans le cas d'un maillage quelconque, il faut définir la position de chaque nœud, et la composition de chaque polygone ou polyèdre ; la définition est dite explicite ;
• dans le cas d'un maillage régulier, la composition des polygones/polyèdres, voire la position des points, peut être déduites d'une règle de construction, on a une définition dite implicite.

Le cas le plus simple d'un maillage régulier est un empilement de parallélépipèdes rectangles tous identiques ; il suffit de définir :

• un nœud du maillage, appelé « origine » ;
• l'orientation des axes des arêtes ;
• la taille des arêtes selon les trois axes ;
• le nombre d'éléments selon les trois axes.

Par contre, ceci n'est possible que pour des formes ayant des contours simples, de type cylindres (au sens large, incluant les prismes). On peut, si nécessaire, diviser un domaine en sous-domaines ayant des formes simples, et donc avoir plusieurs maillages réguliers, ou bien avoir un maillage régulier au cœur du volume, et avoir une « couche » composée de primes et tétraèdres à proximité de la surface.

Le maillage le plus simple à réaliser est un découpage en triangles (2D) ou tétraèdres (3D).

Il existe également des logiciels de morphing qui permettent la modification d'un maillage pour diverses utilités. Cette technique est surtout utilisée par les péons, qui se doivent de respecter les maîtres en maillages travaillant principalement sur Autogrid. Toutefois, le logiciel de déformation de maillage RBF Morph nécessite une connaissance accrue des maillages car il propose des options de morphing préçises afin de correctement conserver les élements et ainsi éviter de détériorer la qualité du maillage.

Utilisation d'un maillage

Un calcul nécessite avant d'être lancé sur un maillage :

• la vérification des paramètres à respecter du modèle éléments finis
• la pose de conditions aux limites

et permet alors d'approcher et simuler des comportements, éventuellement sur sollicitation, du système, d’où le nom méthode approchée.

Logiciels

Il existe des logiciels de maillage (couramment appelés mailleurs). Ce type de logiciel est fréquemment employé en simulation numérique dans la construction du modèle géométrique, avant sa résolution par un code de calcul, mais aussi parfois en modélisation 3D (graphisme, jeux vidéo, etc.).

À titre d'exemple :

• Gambit
• Gmsh (logiciel libre de maillage par éléments finis)
• MeshLab (logiciel libre de traitement de maillages 3D)
• CM2 MeshTools (bibliothèque C++ de mailleurs 1D, 2D, 2,5D et 3D)

Voir aussi

Articles connexes

Liens externes

• Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue !

Bibliographie

• Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue !

Notes et références

• Cet article est partiellement ou en totalité issu de l'article intitulé « Mailleur » (voir la liste des auteurs).

• Portail de l’informatique