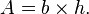Parallélogramme
 |
Cet article ou cette section concernant les mathématiques doit être recyclé. Une réorganisation et une clarification du contenu est nécessaire.
Discutez des points à améliorer en page de discussion.
|
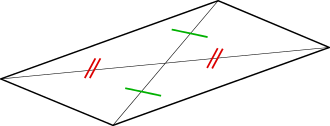
En géométrie, un parallélogramme est un quadrilatère dont les côtés opposés sont parallèles deux à deux.
Définitions équivalentes
Un quadrilatère est un parallélogramme (au sens défini en introduction) si et seulement s'il satisfait l'une des propriétés équivalentes suivantes :
- ses diagonales se coupent en leurs milieux ;
- il est non croisé et ses côtés opposés sont de même longueur deux à deux ;
- il est convexe et ses angles opposés ont la même mesure deux à deux ;
- ses angles consécutifs sont supplémentaires deux à deux ;
- c'est un trapèze (non croisé) dont les bases ont même longueur.
Propriétés
Tout parallélogramme a un centre de symétrie : le point d'intersection de ses diagonales.
Cas particuliers
- Un losange est un parallélogramme ayant au moins deux côtés consécutifs de même longueur. Il est même équilatéral.
- Un rectangle est un parallélogramme ayant au moins un angle droit. Il est même équiangle.
- Un carré est un losange rectangle.
Caractérisation vectorielle
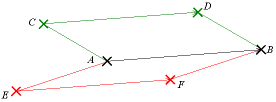
La notion de parallélogramme permet de définir la relation d'équipollence de deux bipoints, ce qui amène à la notion de vecteur en géométrie euclidienne :
- on appelle bipoint tout couple de points (l'ordre des points a une importance) ;
- deux bipoints (A,B) et (C,D) sont dits équipollents si ABCD est un parallélogramme, éventuellement aplati ;
- on peut dire de manière équivalente que (A,B) et (C,D) sont équipollents si [AD] et [BC] ont le même milieu (ce qui règle le problème des parallélogrammes aplatis) ;
- dans ce cas, les segments [AB] et [CD] sont parallèles et de même longueur, mais pas seulement : ils ont aussi « le même sens ».
- La relation d'équipollence est une relation d'équivalence.
- on appelle vecteur
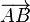la classe d'équivalence du bipoint (A,B), c'est-à-dire l'ensemble des bipoints équipollents à (A,B).
Ainsi, un quadrilatère ABCD est un parallélogramme si et seulement si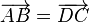 
.
Aire
Soient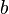 
la longueur d'un côté du parallélogramme et 
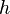la longueur de la hauteur associée. L'aire 
du parallélogramme vaut :
L'aire d'un parallélogramme est aussi donnée par un déterminant.
Antiparallélogramme
Un antiparallélogramme est un quadrilatère croisé dont les côtés opposés ont la même longueur deux à deux.
Dans un antiparallélogramme, les angles opposés ont la même mesure en valeur absolue.
Voir aussi
- Aire d'un polygone
- Parallélépipède
- Paralléloèdre (en)
- Parallélogone (en)
- Théorème de Varignon
Portail de la géométrie