Machine de Turing

Une machine de Turing est un modèle abstrait du fonctionnement des appareils mécaniques de calcul, tel un ordinateur et sa mémoire. Ce modèle a été imaginé par Alan Turing en 1936, en vue de donner une définition précise au concept d’algorithme ou de « procédure mécanique ». Il est toujours largement utilisé en informatique théorique, en particulier dans les domaines de la complexité algorithmique et de la calculabilité.
La thèse de Church postule que tout problème de calcul fondé sur une procédure algorithmique peut être résolu par une machine de Turing. Cette thèse n'est pas un énoncé mathématique, puisqu'elle ne suppose pas une définition précise des procédures algorithmiques. En revanche, il est possible de définir une notion de « système acceptable de programmation » et de démontrer que le pouvoir de tels systèmes est équivalent à celui des machines de Turing (Turing-complet).
À l'origine, le concept de machine de Turing, inventé avant l'ordinateur, était censé représenter une personne virtuelle exécutant une procédure bien définie, en changeant le contenu des cases d'un tableau infini, en choisissant ce contenu parmi un ensemble fini de symboles. D'autre part, la personne doit mémoriser un état particulier parmi un ensemble fini d'états. La procédure est formulée en termes d'étapes très simples, du type : « si vous êtes dans l'état 42 et que le symbole contenu sur la case que vous regardez est '0', alors remplacer ce symbole par un '1', passer dans l'état 17, et regarder une case adjacente (droite ou gauche) ».
Définition
Quoique son nom de « machine » puisse conduire à croire le contraire, une machine de Turing est un concept abstrait, c'est-à-dire un objet mathématique.
Une machine de Turing comporte les éléments suivants :
- un ruban divisé en cases consécutives. Chaque case contient un symbole parmi un alphabet fini. L'alphabet contient un symbole spécial « blanc » ('0' dans les exemples qui suivent), et un ou plusieurs autres symboles. Le ruban est supposé être de longueur infinie vers la gauche ou vers la droite, en d'autres termes la machine doit toujours avoir assez de longueur de ruban pour son exécution. On considère que les cases non encore écrites du ruban contiennent le symbole « blanc » ;
- une tête de lecture/écriture qui peut lire et écrire les symboles sur le ruban, et se déplacer vers la gauche ou vers la droite du ruban ;
- un registre d'état qui mémorise l'état courant de la machine de Turing. Le nombre d'états possibles est toujours fini, et il existe un état spécial appelé « état de départ » qui est l'état initial de la machine avant son exécution ;
- une table d'actions qui indique à la machine quel symbole écrire, comment déplacer la tête de lecture ('G' pour une case vers la gauche, 'D' pour une case vers la droite), et quel est le nouvel état, en fonction du symbole lu sur le ruban et de l'état courant de la machine. Si aucune action n'existe pour une combinaison donnée d'un symbole lu et d'un état courant, la machine s'arrête.
Définition formelle
Plusieurs définitions formelles proches les unes des autres peuvent être données d'une machine de Turing. L'une d'elles, relativement courante, est choisie ici.
Une machine de Turing est un septuplet 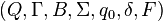 où
où
-
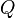 est un ensemble fini d'états ;
est un ensemble fini d'états ; -
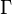 est l'alphabet de travail des symboles de la bande;
est l'alphabet de travail des symboles de la bande; -
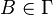 est un symbole particulier (dit blanc) ;
est un symbole particulier (dit blanc) ; -
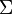 est l'alphabet des symboles en entrée (
est l'alphabet des symboles en entrée (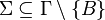 ) ;
) ; -
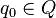 est l'état initial ;
est l'état initial ; -
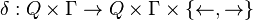 est la fonction de transition ;
est la fonction de transition ; -
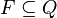 est l'ensemble des états acceptants (ou finaux, terminaux).
est l'ensemble des états acceptants (ou finaux, terminaux).
Les flèches dans la définition de 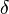 représentent les deux déplacements possibles de la tête de lecture, à savoir le déplacement à gauche et le déplacement à droite. La signification de cette fonction de transition peut être expliquée sur l'exemple suivant :
représentent les deux déplacements possibles de la tête de lecture, à savoir le déplacement à gauche et le déplacement à droite. La signification de cette fonction de transition peut être expliquée sur l'exemple suivant :
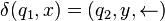 signifie que si la machine de Turing est dans l'état
signifie que si la machine de Turing est dans l'état 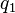 et qu'elle lit le symbole
et qu'elle lit le symbole  , elle écrit
, elle écrit 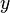 à la place de
à la place de  , va dans l'état
, va dans l'état 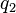 , et déplace sa tête de lecture vers la gauche.
, et déplace sa tête de lecture vers la gauche.
Le fonctionnement de la machine de Turing est alors le suivant. À chaque étape de son calcul, la machine évolue en fonction de l'état dans lequel elle se trouve, et du symbole inscrit dans la case du ruban où se trouve la tête de lecture. Ces deux informations permettent la mise à jour de l'état de la machine grâce à la fonction de transition. À l'instant initial, la machine se trouve dans l'état 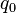 , et le mot inscrit sur le ruban est l'entrée du programme. La machine s'arrête lorsqu'elle rentre dans un état terminal. Le résultat du calcul est alors le mot inscrit sur le ruban.
, et le mot inscrit sur le ruban est l'entrée du programme. La machine s'arrête lorsqu'elle rentre dans un état terminal. Le résultat du calcul est alors le mot inscrit sur le ruban.
L'exemple suivant utilise une version très légèrement différente de machine de Turing dans laquelle une machine s'arrête si elle est dans un état terminal, et que le caractère écrit sur le ruban est le bon (ici le blanc).
Exemple
La machine de Turing qui suit possède un alphabet {‘0’, ‘1’}, ‘0’ étant le « blanc ». On suppose que le ruban contient une série de ‘1’, et que la tête de lecture/écriture se trouve initialement au-dessus du ‘1’ le plus à gauche. Cette machine a pour effet de doubler le nombre de ‘1’, en intercalant un ‘0’ entre les deux séries. Par exemple, « 111 » devient « 1110111 ».
L’ensemble d’états possibles de la machine est {e1, e2, e3, e4, e5} et l’état initial est e1.
La table d’actions est la suivante :
| Ancien état | Symbole lu | Symbole écrit | Mouvement | Nouvel état |
|---|---|---|---|---|
| e1 | 0 | (Arrêt) | ||
| 1 | 0 | Droite | e2 | |
| e2 | 1 | 1 | Droite | e2 |
| 0 | 0 | Droite | e3 | |
| e3 | 1 | 1 | Droite | e3 |
| 0 | 1 | Gauche | e4 | |
| e4 | 1 | 1 | Gauche | e4 |
| 0 | 0 | Gauche | e5 | |
| e5 | 1 | 1 | Gauche | e5 |
| 0 | 1 | Droite | e1 | |
L’exécution de cette machine pour une série de deux '1' serait (la position de la tête de lecture/écriture sur le ruban est inscrite en caractères gras et rouges) :
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Le comportement de cette machine peut être décrit comme une boucle :
- Elle démarre son exécution dans l’état e1, remplace le premier 1 par un 0.
- Puis elle utilise l’état e2 pour se déplacer vers la droite, en sautant les 1 (un seul dans cet exemple) jusqu'à rencontrer un 0 (ou un blanc), et passer dans l'état e3.
- L’état e3 est alors utilisé pour sauter la séquence suivante de 1 (initialement aucun) et remplacer le premier 0 rencontré par un 1.
- L'état e4 permet de revenir vers la gauche jusqu’à trouver un 0, et passer dans l’état e5.
- L'état e5 permet ensuite à nouveau de se déplacer vers la gauche jusqu’à trouver un 0, écrit au départ par l’état e1.
- La machine remplace alors ce 0 par un 1, se déplace d’une case vers la droite et passe à nouveau dans l’état e1 pour une nouvelle itération de la boucle.
Ce processus se répète jusqu’à ce que e1 tombe sur un 0 (c’est le 0 du milieu entre les deux séquences de 1) ; à ce moment, la machine s’arrête.
Machines de Turing universelles
Comme Alan Turing le montre dans son article fondateur, il est possible de créer une machine de Turing qu'on appelle « machine de Turing universelle » et qui est capable de « simuler » le comportement de n'importe quelle autre machine de Turing. « Simuler » signifie que si la machine de Turing universelle reçoit en entrée un codage d'une machine T et des données D elle produit le même résultat que la machine T à la laquelle on donnerait en entrée les données D.
Une machine de Turing universelle a potentiellement la capacité de calculer tout ce qui est calculable, on dit alors qu'elle est Turing-complète. En lui fournissant le codage adéquat, elle peut simuler toute fonction récursive, analyser tout langage récursif, et accepter tout langage partiellement décidable. Selon la thèse de Church-Turing, les problèmes résolubles par une machine de Turing universelle sont exactement les problèmes résolubles par un algorithme ou par une méthode concrète de calcul.
Réalisations de la machine de Turing
Il est assez aisé de simuler une machine de Turing sur un ordinateur moderne, mais il y a une contrainte ! En effet alors que la mémoire d'un ordinateur est finie celle d'une machine de Turing est infinie. Ainsi la machine de Turing n'engendrera pas de débordement mémoire (en) tandis qu'un ordinateur pourra le faire.

Il est aussi possible de construire des machines de Turing purement mécaniques. La machine de Turing, objet de pensée, a pu ainsi être réifiée à de nombreuses reprises en utilisant des techniques parfois assez originales, dont voici quelques exemples :
- En avril 2011, Jim MacArthur a réalisé une machine de Turing mécanique compacte, à 5 symboles, avec des roulements à billes comme support d'informations sur le ruban[1].
- En mars 2012, à l’occasion de l’année Turing (en), une équipe d'étudiants de l'École normale supérieure de Lyon a aussi réalisé une machine de Turing entièrement faite de pièces Lego sans électronique[2],[3].

- Un prototype expérimental pour concrétiser des machines de Turing, (électro-mécanique : réalisée avec les technologies de l'époque de Turing), avec un ruban circulaire et relativement facilement programmable. Conçue en deux parties transportables, elle peut être utilisée pour des présentations et des cours[4].
Références et bibliographie
Références
Bibliographie
- (fr) O. Carton, Langages formels, calculabilité et complexité. Vuibert 2008, ISBN 978-2-7117-2077-4
 ;
; - (fr) J.-M. Autebert, Calculabilité et décidabilité. Dunod 1992, ISBN 978-2-225-82632-0
 ;
; - (fr) É. Jacopin, Les machines de Turing -- Introduction à la caractérisation de la complexité d'un problème. Cépaduès 2009, ISBN 978-2-85428-865-0
 ;
; - Alan Turing, Jean-Yves Girard, La machine de Turing, Éditions du Seuil, [détail de l’édition] ; cet ouvrage comprend notamment une traduction en français (par Julien Basch et Patrice Blanchard) de l'article original, ainsi qu'une correction par Emil Post des erreurs y figurant ;
- (en) Alan Turing, On Computable Numbers, with an Application to the Entscheidungsproblem, vol. 2:42, coll. « Proceedings of the London Mathematical Society », (lire en ligne), p. 230-265 ;
- (fr) Alan Turing, Précis of ‘Computable Numbers’ (lire en ligne).
![]() : document utilisé comme source pour la rédaction de cet article.
: document utilisé comme source pour la rédaction de cet article.
Voir aussi
Articles connexes
- Machine de Turing non-déterministe ;
- Machine de Turing probabiliste ;
- Machine de Blum-Shub-Smale : une généralisation à des machines calculant sur
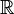 ;
; - Problème de la décision ;
- Expérience de pensée.
Liens externes
- (en) Web Turing Machine Application Web pour construire et exécuter des machines de Turing (Javascript)
- Machine de Turing, une applet java simulant des machines de Turing.
- Simulateur de machines de Turing, un simulateur en ligne de machines de Turing.
- Le film "La Machine de Turing réalisée" de Christophe Gombert et Hugo Deboise à visionner en ligne gratuitement.
- Machine expérimentale pour simuler des machines de Alan Turing avec 12 états et programmable sur une idée d'Olivier Raynaud du laboratoire LIMOS de l'Université Blaise Pascal
- Le génie interrompu d'Alan Turing : présentation et bibliographie d'une conférence BnF de Bernard Chazelle, programmée pour le 19 mars 2014
- Portail de l'informatique théorique