Calculabilité

Cet article est une ébauche concernant l’informatique, la logique et les mathématiques. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

La théorie de la calculabilité (appelée aussi parfois théorie de la récursion) est une branche de la logique mathématique et de l'informatique théorique. Alors que la notion intuitive de fonction calculable est aussi vieille que les mathématiques (voir l'article Histoire des mathématiques), la formalisation de ces notions a commencé dans la décennie 1930 afin de répondre à des problèmes fondamentaux de logique mathématique, dont celui énoncé par David Hilbert et appelé Entscheidungsproblem ou problème de la décision.

La calculabilité cherche d'une part à identifier la classe des fonctions qui peuvent être calculées à l'aide d'un algorithme et d'autre part à appliquer ces concepts à des questions fondamentales des mathématiques. Une bonne appréhension de ce qui est calculable et de ce qui ne l'est pas permet de voir les limites des problèmes que peuvent résoudre les ordinateurs.

Définition d'une fonction calculable

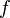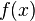Intuitivement, une fonction est une fonction calculable s'il existe une méthode précise qui, étant donné un argument , permet d'obtenir l'image en un nombre fini d'étapes. Plusieurs formalisations mathématiques de ce que peut être une méthode de calcul existent et on peut montrer qu'un grand nombre d'entre elles (fonctions récursives, machine de Turing, lambda-calcul, machine à compteurs, automate cellulaire, etc.) sont équivalentes, c'est-à-dire qu'elles définissent exactement les mêmes fonctions calculables. Formellement, une fonction calculable est donc une fonction calculable selon l'une de ces définitions, par exemple le lambda-calcul^[1].

La thèse de Church énonce que les définitions mathématiques équivalentes ci-dessus capturent bien le concept intuitif de méthode de calcul fonctionnant en temps fini.

Existence de fonctions non calculables

Il peut être démontré qu'il existe des fonctions 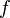qui sont incalculables, c’est-à-dire dont, étant donné , la valeur 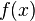ne peut être calculée en un temps fini par aucun algorithme que l'on aurait associé à 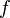. En effet il y a un nombre dénombrable d'algorithmes (un algorithme peut toujours être représenté par un mot fini sur un alphabet fini), donc il y a seulement un nombre dénombrable de fonctions calculables. En revanche, les fonctions (partielles ou pas) sur un domaine infini ne sont pas dénombrables, de par le théorème de Cantor^[2]. Ceci fournit une preuve de l'existence de fonctions incalculables.

On connaît de nombreux exemples explicites de fonctions incalculables. Le plus courant est celui du problème de l'arrêt : il n'existe pas de programme universel qui prenne n'importe quel programme en argument et qui, en temps fini, renvoie « oui » si l'exécution du programme reçu en argument finit par s'arrêter et « non » s'il ne finit pas. Un autre exemple d'une fonction non calculable, plus perturbante dans un certain sens, est celle dite du castor affairé. Il s'agit d'une fonction bien définie, ayant des valeurs pour chaque entier, mais dont on ne peut pas calculer la valeur. Gregory Chaitin a introduit un nombre Ω qui a, entre autres, la particularité d'être parfaitement défini, mais dont la suite des décimales ne peut pas être donnée par une fonction calculable.

Modèles de calcul

Plusieurs modèles de calcul sont utilisés en calculabilité :

• les fonctions récursives ;
• le lambda-calcul ;
• les machines de Turing ;
• les machines à compteurs ;
• les automates cellulaires ;
• les circuits booléens
• les machines parallèle à accès arbitraire ou PRAM ;
• les Random access machines ou RAM;
• les machines de Blum-Shub-Smale.

Malgré la diversité de ces modèles, la classe de fonctions calculables par chacun de ceux-ci est unique et cette constatation est le fondement de la thèse de Church.

Notes

1. ↑ Historiquement, la première caractérisation formelle et mathématique des algorithmes (Origins of Recursive Function Theory dans Annals of the History of Computing, Vol. 3 No. 1, janvier 1981).
2. ↑ Peut-on tout programmer ? Cours de l'université de Lille

Références

• Olivier Carton, Langages formels, calculabilité et complexité,‎ 2008 [détail de l’édition] (lire en ligne)
• Jean-Michel Autebert, Calculabilité et décidabilité, Dunod, 1992 (ISBN 978-2225826320)
• Pierre Wolper, Introduction à la calculabilité, Dunod, 2006, 3^e éd. (ISBN 978-2100499816)
• (en) George Boolos, John P. Burgess (en) et Richard Jeffrey (en), Computability and Logic, Cambridge, 2007, 5^e éd. (ISBN 978-0521701464)

Voir aussi

Articles connexes

• Portail de l'informatique théorique
• Portail de la logique
• Portail des mathématiques