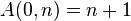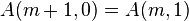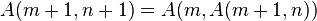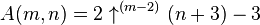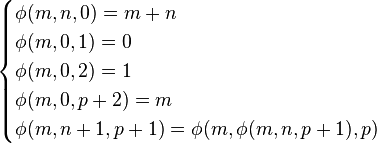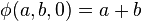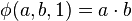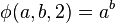Fonction d'Ackermann

Dans la théorie de la récursivité, la fonction d'Ackermann (aussi appelée fonction d'Ackermann-Péter) est un exemple simple de fonction récursive non récursive primitive, trouvée en 1926 par Wilhelm Ackermann. Elle est souvent présentée sous la forme qu'en a proposée la mathématicienne Rózsa Péter, comme une fonction à deux paramètres entiers naturels comme arguments et qui retourne un entier naturel comme valeur, noté en général A(m, n).

Histoire

Dans les années 1920, Wilhelm Ackermann et Gabriel Sudan, alors étudiants sous la direction de David Hilbert, étudiaient les fondements de la calculabilité. Sudan est le premier à donner un exemple de fonction récursive mais non récursive primitive, appelée alors fonction de Sudan. Peu après et indépendamment, en 1928, Ackermann a publié son propre exemple de fonction récursive mais non récursive primitive^[1]. À l'origine, Ackermann considéra une fonction ϕ(m, n, p) dépendant de trois variables, et consistant, si p > 1, à calculer la puissance itérée p – 1 fois de m par n, c'est-à-dire m → n → (p – 1) en notation de Conway.

Ackermann démontra que sa fonction ϕ était bien une fonction récursive, c'est-à-dire une fonction qu'un ordinateur idéalisé peut calculer. Dans Sur l'infini^[2], David Hilbert conjectura que la fonction d'Ackermann n'était pas primitivement récursive. Cette conjecture fut établie par Ackermann lui-même dans son article Zum Hilbertschen Aufbau der reellen Zahlen^[3]. Sur l'infini était l'article le plus important de Hilbert sur les fondements des mathématiques, servant de cœur à son programme pour fixer la base des nombres transfinis.

Une fonction de seulement deux variables — correspondant à ϕ(2, ∙, ∙) — fut donnée plus tard par Rózsa Péter et Raphael Robinson ; c'est cette dernière qui est connue aujourd'hui sous le nom de fonction d'Ackermann.

Définition

La fonction d'Ackermann-Péter est définie récursivement comme suit :

A(m, n) = \begin{cases} n+1 & \mbox{si } m = 0 \\ A(m-1, 1) & \mbox{si } m > 0 \mbox{ et } n = 0 \\ A(m-1, A(m, n-1)) & \mbox{si } m > 0 \mbox{ et } n > 0. \end{cases}

Autrement dit :

A(0, n) = n+1\,

A(m+1, 0) = A(m, 1)\,

A(m+1, n+1) = A(m, A(m+1, n))\,

Elle peut aussi être exprimée avec la notation des flèches de Knuth:

A(m, n) = 2 \uparrow^{(m-2)}(n+3)-3

Ackermann a cependant lui-même initialement donné cette définition à trois paramètres :

\begin{cases} \phi(m, n, 0) = m + n \\ \phi(m, 0, 1) = 0 \\ \phi(m, 0, 2) = 1 \\ \phi(m, 0, p+2) = m \\ \phi(m, n+1, p+1) = \phi(m, \phi(m, n, p+1), p) \end{cases}\,\!

Elle satisfait aux égalités suivantes :

\phi(a, b, 0) = a+b\,

\phi(a, b, 1) = a \cdot b

\phi(a, b, 2) = a^b\,

\ldots

Table de valeurs

Valeurs de A(m, n)
m\n	0	1	2	3	4	n
0	1	2	3	4	5	n + 1
1	2	3	4	5	6	n + 2
2	3	5	7	9	11	2n + 3
3	5	13	29	61	125	2^n + 3 − 3
4	13	65533	2⁶⁵⁵³⁶ − 3	A(3, 2⁶⁵⁵³⁶ − 3)	A(3, A(4, 3))	2^{2^...²} − 3 (n + 3 termes)
5	65533	A(4, 65533)	A(4, A(5, 1))	A(4, A(5, 2))	A(4, A(5, 3))
6	A(5, 1)	A(5, A(5, 1))	A(5, A(6, 1))	A(5, A(6, 2))	A(5, A(6, 3))

Importance épistémologique

La seule opération effectuée lors du déroulement de la fonction d'Ackermann est l'ajout de 1 (lorsque m est nul). Malgré cela, cette fonction croît extrêmement rapidement : A(4,2) a déjà 19729 chiffres, et représente bien plus que le nombre d'atomes estimé dans l'univers. Cette extrême croissance peut être exploitée pour montrer que la fonction f définie par f(n) = A(n, n) croît plus rapidement que n'importe quelle fonction récursive primitive et ainsi que A n'en est pas une.

Cette fonction est néanmoins définissable par récursion primitive d'ordre supérieur, schéma de récursion proposé par le système T de Gödel et ses extensions est calculable par une machine de Turing. La fonction d'Ackermann constitue donc un exemple de fonction récursive, mais non récursive primitive. C'est peut-être l'exemple le plus cité d'une telle fonction (en particulier chez Knuth), et ce pour quoi elle est connue principalement. Son intérêt épistémologique va cependant au delà.

La fonction d'Ackermann montre que la notion de calculabilité introduite par les fonctions récursives primitives ne correspond pas à la notion de calculabilité la plus générale, celle mentionnée par la thèse de Church. En effet, la fonction d'Ackermann est calculable au sens de Turing et de Church, mais pas par une fonction récursive primitive. Cet exemple montre que la thèse de Church ne concerne pas tous les systèmes de calcul. Les fonctions récursives primitives permettent bien de définir la plupart des fonctions usuelles, mais ne sont pas équivalentes aux machines de Turing ou au lambda-calcul. La calculabilité de la fonction d'Ackermann sert ici de critère distinctif, ce qui fait son importance épistémologique.

Description explicite

Intuitivement, la fonction d'Ackermann génère progressivement une multiplication par deux (additions réitérées), une exponentiation de base 2 (multiplications réitérées), une exponentiation réitérée, une réitération de cette opération, et ainsi de suite. Elle peut être exprimée en utilisant la notation des puissances itérées de Knuth :

A(1, n) = 2 + (n + 3) – 3

A(2, n) = 2 × (n + 3) – 3

A(3, n) = 2 ^ (n + 3) – 3

A(4, n) = 2 ↑↑ (n + 3) – 3

A(5, n) = 2 ↑↑ (2 ↑↑ (2 ↑↑ (... ↑↑2))) – 3 (n + 3 deux)

= 2↑↑↑(n + 3) – 3

A(6, n) = 2↑↑↑↑(n + 3) – 3, etc.

On montre assez facilement par récurrence que :

A(u, v) = 2↑^(u–2)(v + 3) – 3 = ϕ(2, v + 3, u – 1) – 3.

Réciproque

L'inverse de la fonction d'Ackermann est aussi utilisée. Puisque la fonction f définie par f(n) = A(n,n) considérée précédemment croît réellement très vite, sa réciproque croît vraiment très lentement. Elle apparaît notamment en algorithmique, pour exprimer des complexités. Dans ce domaine elle est souvent notée 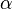$\alpha$ ^[4]. On la trouve par exemple dans l'analyse de certaines structures de données comme l'Union-Find, dans un algorithme de calcul de l'arbre couvrant de poids minimal et en géométrie algorithmique^[4]. Elle peut être définie simplement sans faire appel à la fonction d'Ackermann, en définissant la hiérarchie inverse d'Ackermann (qui fait aussi apparaître le logarithme itéré)^[4]^,^[5].

Applications pratiques

La fonction d'Ackermann demandant beaucoup de calculs même pour de petites entrées, elle est parfois utilisée comme programme de test d'une implémentation d'un langage de programmation : en particulier, elle utilise de façon très exigeante la récursivité, de même que ses consœurs fib (suite de Fibonacci) et tak (fonction de Takeuchi).

En plus de tester directement les performances d'un langage de programmation, la fonction d'Ackermann a été utilisée comme exemple pour étudier des transformations de programme et des optimisations, en particulier dans le domaine de la spécialisation de programmes et de l'évaluation partielle (en)^[6].

Références

↑ (en)Cristian Calude, Solomon Marcus et Ionel Tevy, « The first example of a recursive function which is not primitive recursive », Historia Math., vol. 6, n^o 4, 1979, p. 380-384.
↑ (de) David Hilbert, « Über das Unendliche », Mathematische Annalen, vol. 95,‎ 1926, p. 161-190 (lire en ligne), trad. : (en) On the infinite et André Weil, « Sur l'infini », Acta Mathematica, vol. 48, n^o 1-2,‎ 1926, p. 91-122 (DOI 10.1007/BF02629757).
↑ (de) Wilhelm Ackermann, « Zum Hilbertschen Aufbau der reellen Zahlen », Mathematische Annalen, vol. 99,‎ 1928, p. 118-133 (lire en ligne).
1 2 3 Gabriel Nivasch, « Inverse Ackermann without pain »,‎ 2009.
↑ Raimund Seidel, « Understanding the inverse Ackermann function », sur 22nd European Workshop on Computational Geometry,‎ 2006.
↑ (en) Yanhong A. Liu et Scott D. Stoller, « Optimizing Ackermann's Function by Incrementalization », Workshop on Partial Evaluation and Semantics Based Program Manipulation, 2003.

Voir aussi

Liens externes

Implémentation dans divers langages de programmation sur rosettacode.org
La course aux grands nombres de Scott Aaronson, traduit sur le blog smwhr, et sa version originale : Who can name the biggest number? (1999), un essai sur la notion de grand nombre.

Portail de la logique
Portail de l'informatique théorique

This article is issued from Wikipédia - version of the Wednesday, September 30, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.