Système binaire

Pour les articles homonymes, voir Système binaire (astronomie) et Binaire.

Exemple d'informations binaires.

Le système binaire est un système de numération utilisant la base 2. On nomme couramment bit (de l'anglais binary digit, soit « chiffre binaire ») les chiffres de la numération binaire positionnelle. Ceux-ci ne peuvent prendre que deux valeurs, notées par convention 0 et 1.

C'est un concept essentiel de l'informatique. En effet, les processeurs des ordinateurs actuels sont composés de transistors ne gérant chacun que deux états.

Un calcul informatique n'est donc qu'une suite d'opérations sur des paquets de 0 et de 1, appelés octets lorsqu'ils sont regroupés par huit.

Définition

Le système binaire le plus courant est l'équivalent en base deux de la numération de position que nous utilisons en base dix dans la vie courante.

Dans ce type de codage, chaque nombre est représenté de façon unique par une suite ordonnée de chiffres. Et chaque chiffre représente une puissance de la base. Si on se limite dans un premier temps aux nombres entiers positifs, en base dix ces puissances sont : un (1), dix (représenté par 10), cent (dix fois dix, représenté par 100), mille (dix fois cent, représenté par 1000), dix mille etc. En base deux, ces puissances sont : un (1), deux (représenté lui aussi par 10), quatre (deux fois deux, représenté par 100), huit (deux fois quatre, représenté par 1000), seize (deux fois huit, représenté par 10000) etc.

On voit que la signification des représentations 10, 100, 1000, etc. dépend de la base utilisée : 10 est toujours égal à la base, c'est-à-dire dix en base dix, mais deux en base deux.

En base dix, on a besoin de dix chiffres, de zéro à neuf ; en base n, on a besoin de n chiffres, de zéro à n – 1 ; en particulier en base deux, on a besoin de deux chiffres : zéro et un.

Un nombre qui s'exprime en base B par les quatre chiffres 1101 s'analyse :

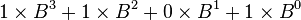$1\times B^3+1\times B^2+0\times B^1+1\times B^0$ , qui donne :

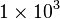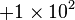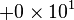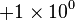1101 en base B = 10 :	$1\times 10^3$	$+1\times 10^2$	$+0\times 10^1$	$+1\times 10^0$	$=1101$
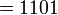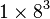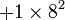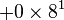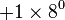1101 en base B = 8 :	$1\times 8^3$	$+1\times 8^2$	$+0\times 8^1$	$+1\times 8^0$	$=577$
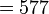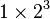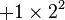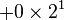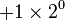1101 en base B = 2 :	$1\times 2^3$	$+1\times 2^2$	$+0\times 2^1$	$+1\times 2^0$	$=13$

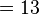Énumération des premiers nombres

Les premiers nombres, et chiffres de la base de numération 10, s'écrivent :

décimal	binaire	commentaire
0	0	zéro
1	1	un = base puissance zéro (valable pour toutes les bases, donc deux et dix)
2	10	deux = deux puissance un (un zéro derrière le 1)
3	11
4	100	quatre = deux puissance deux (deux zéro derrière le 1)
5	101
6	110
7	111
8	1000	huit = deux puissance trois (trois zéro derrière le 1)
9	1001

Opérations

Les techniques des quatre opérations de base (addition, soustraction, multiplication et division) restent exactement les mêmes qu'en notation décimale, elles sont juste simplifiées de façon drastique parce qu'il n'y a que deux chiffres (zéro et un). Pour la multiplication par exemple, quelle que soit la base, la multiplication par 10 (c’est-à-dire par la base elle-même)^[1] se fait en ajoutant un zéro à droite.

Seules changent d'une part la forme de la suite de chiffres qui exprime le résultat (elle ne compte que des zéros et un), d'autre part la signification de cette suite (10 signifie « deux » et non « dix », 100 signifie « quatre » et non « cent », etc.).

exemples : additions, soustractions

On passe d'un nombre binaire au suivant en ajoutant 1, comme en décimal, sans oublier les retenues et en utilisant la table ordinaire (mais réduite à sa plus simple expression) :

 0 + 0 = 0    0 + 1 = 1    1 + 0 = 1   1 + 1 = 0 avec 1 retenue
 0 - 0 = 0    0 - 1 = 1 avec 1 retenue   1 - 0 = 1   1 - 1 = 0

ainsi:

   11
+   1
 ____
  100

Détail :

1 + 1 = 10           => on pose 0 et on retient 1
1 + 1(retenue) = 10  => on pose 0 et on retient 1
0 + 1(retenue) = 1   => on pose 1 devant 00

Théorie informatique

L'arithmétique binaire (plus simplement le calcul binaire) est utilisé par les systèmes électroniques les plus courants (calculatrices, ordinateurs, etc.) car les deux chiffres 0 et 1 s'y traduisent facilement par la tension ou le passage d'un courant : 0 représentant l'état bas (tension ou courant nul) et 1 l'état haut (tension qui existe, courant qui passe).

Représentation des entiers négatifs

Pour compléter la représentation des entiers, il faut pouvoir écrire des entiers négatifs. La façon informatique de le faire est prévoir un bit de signe, placé en tête. Un bit de signe nul indique une valeur positive, un bit de signe positionné à 1 indique une valeur négative.

Les informaticiens utilisent deux représentations.

Complément à un

Article détaillé : Complément à un.

Ce codage, fort simple, consiste à inverser la valeur de chaque bit composant une valeur binaire.

Par exemple, pour obtenir –7 :

0111 valeur décimale 7
1000 complément à un

Dans ce système, la valeur 0 a deux représentations : « +0 » et « –0 » (dans notre exemple : 0000 et 1111), ce qui oblige à réaliser 2 tests pour tester la valeur nulle d'un résultat.

Complément à deux

Article détaillé : Complément à deux.

Afin de pallier ce défaut, on a introduit la représentation par complément à deux. Celle-ci consiste à réaliser un complément à un de la valeur, puis d'ajouter 1 au résultat.

Par exemple pour obtenir –7 :

0111 codage de 7 en binaire
1000 complément à un
1001 on ajoute 1 : représentation de -7 en complément à deux

Le zéro est représenté seulement par 0000

Ce codage a l'avantage de ne pas nécessiter de différenciation spéciale des nombres positifs et négatifs, et évite en particulier le problème d'ordinateurs anciens (Control Data 6600) qui avaient un « +0 » et un « –0 » dont il fallait « faire comprendre » aux circuits de tests que c'était le même nombre. Voici une addition de –7 et +9 réalisée en complément à deux sur 4 bits :

-7        1001 
+9        1001
__        ____
 2    (1) 0010     (on « ignore » la retenue)

Avec n bits, ce système permet de représenter les nombres entre –2^n–1 et 2^n–1 – 1.

Entre les bases 2, 8 et 16

Du binaire vers octal ou hexadécimal

Les bases 8 (octale) et 16 (hexadécimale) sont des bases multiples de la base 2. Ces deux bases ont été couramment employées en informatique et pour des raisons pratiques; ces bases étant fortement liées à la base 2 et les nombres écrits dans ces bases étant plus « manipulables » (car d'écriture plus courte) par l'intellect humain. L'écriture de nombres dans ces bases est facilement obtenue par regroupement de chiffres de l'écriture du nombre en base 2.

Octal : base 8 = 2³. Il suffit de parcourir le nombre binaire de la droite vers la gauche en regroupant les chiffres binaires 3 par 3 : chaque paquet de 3 (le dernier devant être parfois complété par des 0 à gauche) est l'écriture binaire d'un chiffre en base 8 (0₈ = 000, 1₈ = 001, 2₈ = 010, 3₈ = 011, 4₈ = 100, 5₈ = 101, 6₈ = 110, 7₈ = 111).
- 10101101110₂ va s'écrire 10 101 101 110 et en convertissant la valeur de chacun des blocs en un chiffre octal, on obtient le nombre octal 2556₈.
Hexadécimal : base 16 = 2⁴. Il suffit de parcourir le nombre binaire de la droite vers la gauche en regroupant les chiffres binaires 4 par 4 : chaque paquet de 4 bits est la représentation binaire d'un chiffre en base 16. En base 16, il faut 16 symboles et conventionnellement, on utilise les 10 chiffres décimaux suivis des 6 premiers caractères de l'alphabet selon la règle suivante: A₁₆ = 10₁₀ = 1010₂, B₁₆ = 11₁₀ = 1011₂, C₁₆ = 12₁₀ = 1100₂, D₁₆ = 13₁₀ = 1101₂, E₁₆ = 14₁₀ = 1110₂ et F₁₆ = 15₁₀ = 1111₂.
- 10101101110₂ va s'écrire 101 0110 1110 et en convertissant la valeur de chacun des blocs en décimal on obtient : 5, 6, 14 c'est-à-dire 56E₁₆.

On pourrait facilement étendre ce principe à toutes les bases qui sont puissances de 2.

Vers le binaire

Il suffit de convertir la valeur de chacun des chiffres sous leur forme binaire.

1A2F₁₆ va s'écrire 1, 10 = 8 + 2, 2, 15 = 8 + 4 + 2 + 1 soit 0001 1010 0010 1111₂
156₈ va s'écrire 1, 5 = 4 + 1, 6 = 4 + 2 soit 1 101 110₂

Table des valeurs des groupements de chiffres binaires

Binaire	Décimal	Octal	Hexadécimal
0000	0	0	0
0001	1	1	1
0010	2	2	2
0011	3	3	3
0100	4	4	4
0101	5	5	5
0110	6	6	6
0111	7	7	7

Binaire	Décimal	Octal	Hexadécimal
1000	8	10	8
1001	9	11	9
1010	10	12	A
1011	11	13	B
1100	12	14	C
1101	13	15	D
1110	14	16	E
1111	15	17	F

Code de Gray ou binaire réfléchi

Article détaillé : code de Gray.

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue !

Ce codage permet de ne faire changer qu'un seul bit à la fois quand un nombre est incrémenté ou décrémenté d'une unité.

Le code de Gray, également appelé binaire réfléchi, permet de ne faire changer qu'un seul bit à la fois quand un nombre est incrémenté ou décrémenté d'une unité. Le nom du code vient de l'ingénieur américain Frank Gray qui déposa un brevet sur ce code en 1947^[2]. Louis Gros, qui fut clerc de notaire puis conseiller à la Cour d'appel de Lyon, publia en 1872 un opuscule, Théorie du baguenodier par un clerc de notaire lyonnais, où ce code était présenté pour la première fois en lien avec un casse-tête, le jeu du baguenaudier^[3].

codage binaire classique		Codage Gray ou binaire réfléchi
0	0000	0	0000
1	0001	1	0001
2	0010	2	0011
3	0011	3	0010
4	0100	4	0110
5	0101	5	0111
6	0110	6	0101
7	0111	7	0100

Pour « calculer » directement le code de Gray d'un entier à partir de celui de son prédécesseur on peut procéder ainsi :

lorsqu'il y a un nombre pair de 1 on inverse le dernier bit

lorsqu'il y a un nombre impair de 1 on inverse le bit directement à gauche du 1 le plus à droite.

Le code de Gray est utilisé entre autres sur une roue codeuse.

Décimal codé binaire (« binary coded decimal », ou BCD)

Article détaillé : Décimal codé binaire.

Afin de concilier la logique binaire de l'ordinateur avec la logique humaine, on peut convertir en binaire, plutôt que les nombres eux-mêmes, chacun des chiffres qui les composent en notation décimale positionnelle. Chacun de ces chiffres est alors codé 4 bits :

1994 =  0001    1001   1001   0100
      1×1000 + 9×100 + 9×10 + 4×1

Avec n bits (n multiple de 4), il est possible de représenter les nombres entre 0 et 10^n/4-1. Soit approximativement entre 0 et 1.778ⁿ-1. Le BCD est un code redondant, en effet certaines combinaisons ne sont pas utilisées (comme 1111 par exemple).

Cette représentation évite par construction tous les problèmes gênants de cumul d'arrondi qui interviendraient lors de la manipulation de grands nombres dépassant la taille des circuits en arithmétique entière et obligent à recourir au flottant. Il est cependant possible de manipuler des nombres à précision arbitraire en utilisant un codage plus efficace que le BCD.

Il existe des variantes du codage BCD :

code Aiken où 0, 1, 2, 3, 4 sont codés comme en BCD et 5, 6, 7, 8, 9 sont codés de 1011 à 1111. Il permet d'obtenir le complément à 9 en permutant les 1 et les 0.
codage binaire excédant 3 qui consiste à représenter le chiffre à coder + 3.

Applications

Théorie de l'information

Article détaillé : Entropie de Shannon.

En théorie de l'information, l'entropie d'une source d'information est exprimée en bits. La théorie elle-même est indifférente à la représentation des grandeurs qu'elle utilise.

Logique

La logique classique est une logique bivalente: une proposition est soit vraie, soit fausse. Il est donc possible de représenter la vérité d'une proposition par un chiffre binaire. On peut par exemple modéliser les opérations de l'arithmétique binaire à l'aide de l'algèbre de Boole.

L'algèbre de Boole représente un cas très particulier d'usage des probabilités ne faisant intervenir que les seules valeurs de vérité 0 et 1. Voir Théorème de Cox-Jaynes.

Informatique

Le binaire est utilisé en informatique car il permet de modéliser le fonctionnement des composants de commutation comme le TTL ou le CMOS. La présence d'un seuil de tension aux bornes des transistors, en négligeant la valeur exacte de cette tension, représentera 0 ou 1. Par exemple le chiffre 0 sera utilisé pour signifier une absence de tension à 0,5V près, et le chiffre 1 pour signifier sa présence à plus de 0,5V. Cette marge de tolérance permet de pousser les cadences des microprocesseurs à des valeurs atteignant sans problème (hormis d'échauffement) plusieurs gigahertz.

En informatique, la représentation binaire permet de clairement manipuler des bits : chaque chiffre binaire correspond à un bit. Cependant, la représentation binaire nécessitant l'usage de beaucoup de chiffres (même pour des nombres assez petits), elle entraîne d'importants problèmes de lisibilité et donc de risques d'erreur de transcription pour les programmeurs. On préfère donc d'autres représentations : la notation hexadécimale, qui permet de manipuler l'information par paquets de 4 bits, est adaptée à la quasi-totalité des microprocesseurs actuels travaillant avec des mots de 8, 16, 32 ou 64 bits ; plus rare, la notation octale, populaire du temps des premiers mini-ordinateurs DEC à 12 ou 36 bits, qui permet de représenter l'information par paquets de 3 bits.

63 ₍₁₀₎ = 111111 ₍₂₎ = 77 ₍₈₎ = 3F ₍₁₆₎
64 ₍₁₀₎ = 1000000 ₍₂₎ = 100 ₍₈₎ = 40 ₍₁₆₎
255 ₍₁₀₎ = 11111111 ₍₂₎ = 377 ₍₈₎ = FF ₍₁₆₎
256 ₍₁₀₎ = 100000000 ₍₂₎ = 400 ₍₈₎ = 100 ₍₁₆₎

Histoire

Cet article contient une ou plusieurs listes.

Le texte gagnerait à être rédigé sous la forme de paragraphes synthétiques, plus agréables à la lecture.

3000 av J.C. : traité du Yi Jing sous l'empereur Fou-Hi^[4]
1650 av J.C. : multiplication égyptienne
1600 : Table de Thomas Harriot (1560-1621), première expression du binaire connue en France
1605 : Francis Bacon utilise un code secret bilitère (à deux lettres) pour protéger ses messages (il remplace les lettres du message par leur position en binaire, puis les 0 et les 1 par des A et des B. Exemple : lettre E → 5 → 00101 → codée AABAB
1617 : Neper, dans son traité Rhabdologie, montre comment effectuer simplement les opérations sur des nombres binaires.
1670 : Juan Caramuel y Lobkowitz fait la première étude raisonnée sur les numérations non décimales.
1677 : Leibniz étudie le binaire comme mode de calcul des fractions décimales. De progressione dyadica est daté de 1679^[5]
1688^{[réf. nécessaire]} : la Chine s'empare des idées de Leibniz et redécouvre des travaux chinois datant de 3000 ans av. J.-C.
1703 : Leibniz publie son exposé sur le système binaire devant l'Académie des sciences de Paris dans les Mémoires^[6].
1847 : George Boole publie les premiers travaux de son Algèbre de Boole.
1876 : Mimault dépose le brevet 1301 concernant:
- système télégraphiques multiples, imprimeurs et écrivants basés sur des combinaisons mécaniques ou graphiques provenant de « (X + 1) puissance m »
- système télégraphiques multiples, imprimeurs et écrivants basés sur des combinaisons de la progression 1 : 2 : 4 : 8 : 16^[7].

Notes et références

↑ Attention : 10 et non dix ; en base deux, 10 vaut deux.
↑ (en) Frank Gray pour Bell Labs, Brevet U.S. 2,632,058 : Pulse code communication, déposé le 13 novembre 1947, publié le 17 mars 1953, sur le site de l'USPTO.
↑ Luc-Agathon-Louis Gros, Théorie du baguenodier par un clerc de notaire lyonnais, Lyon, Aimé Vingtrinier,‎ 1872 (lire en ligne).
↑ Robert Ligonnière, Préhistoire et histoire des ordinateurs, Paris, Robert Laffont,‎ 1987 (ISBN 2-221-05261-7), p. 199.
↑ De la numération binaire, traduction et analyse par Yves Serra du texte de Leibniz, sur BibNum.
↑ Leibniz, « Explication de l’arithmétique binaire », Mémoires de l'Académie des sciences, 1703, p. 85-89.
↑ Description des notes contenues dans le brevet sous plis.

Voir aussi

Liens externes

Convertisseur décimal, hexadécimal, binaire
(en) Convertisseur hexadécimal, décimal, octal, binaire

Portail de la logique
Portail de l’informatique
Portail de la programmation informatique
Portail de l’arithmétique et de la théorie des nombres

This article is issued from Wikipédia - version of the Monday, November 02, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.