Représentation de groupe

En mathématiques, l'idée générale de la théorie des représentations est d'étudier un groupe G en le faisant agir sur un espace vectoriel V de manière linéaire : on essaie ainsi de voir G comme un groupe de matrices (d'où le terme représentation). On peut ainsi, à partir des propriétés relativement bien connues du groupe des automorphismes de V, arriver à déduire quelques propriétés de G.

Réciproquement, en tant qu'objets de la théorie, et non plus comme outil, théorie, on est naturellement amené à la question : Quelle est la dimension minimale des matrices (cas fini) qui font représenter tel sous-groupes de GLn(R); Peut-on alors imposer aux coefficients de la matrice d'être entiers ?

Définitions

Soit G un groupe, K un corps commutatif et V un espace vectoriel sur K. On appelle représentation du groupe G une action linéaire de G sur V, autrement dit un morphisme de groupes de G dans le groupe linéaire GL(V). Plus explicitement, c'est une application

\rho~:~G\to\mathrm{GL}(V)\quad\text{telle que}\quad\rho(g_1)\circ\rho(g_2)=\rho(g_1 g_2).

Pour qu'une application ρ de G dans l'espace des endomorphismes de V vérifiant ρ(g₁)∘ρ(g₂)=ρ(g₁g₂) soit en fait à valeurs dans GL(V), il suffit que l'un des ρ(g) soit un automorphisme.

Pour écrire l'action d'un élément 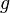$g$ du groupe sur un élément 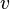$v$ de l'espace vectoriel à travers la représentation 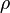$\rho$ , on notera parfois 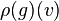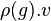$\rho(g)(v)$ , $\rho(g).v$ ou même 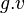$g.v$ s'il n'y a aucune ambiguïté. On note parfois une représentation 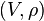$(V,\rho)$ . On dit parfois également (et abusivement) que V est une représentation de G.

Un morphisme de représentations de G, ou « opérateur d'entrelacement », d'une représentation 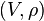$(V,\rho)$ vers une représentation 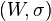$(W,\sigma)$ , est une application K-linéaire φ de V dans W telle que pour tout g appartenant à G on ait

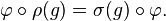
\varphi\circ\rho(g)=\sigma(g)\circ\varphi.

On dit alors aussi que φ est un morphisme G-équivariant de V dans W.

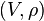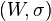Un cas important est celui où φ est un isomorphisme : les représentations $(V,\rho)$ et $(W,\sigma)$ sont dites isomorphes ou équivalentes s'il existe un isomorphisme φ de V dans W qui soit G-équivariant, c'est-à-dire qui vérifie, pour tout g appartenant à G :

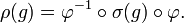
\rho(g)=\varphi^{-1}\circ\sigma(g)\circ\varphi.

V et W ont alors même dimension.

Exemples

La représentation unité de G sur la droite vectorielle K est celle qui à tout élément de G associe l'identité de K.
Si G est un sous-groupe de GL_n(K), G agit naturellement sur Kⁿ. La représentation associée est appelée représentation standard.
Si G est le groupe cyclique fini ℤ/nℤ, la donnée d'une représentation de G sur V équivaut au choix d'un élément f de GL(V) tel que f ⁿ = id_V.
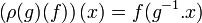
À partir d'une action de G sur un ensemble X, on peut définir une représentation de G sur l'espace K^X des applications de X dans K, en posant : $\left(\rho(g)(f)\right)(x)=f(g^{-1}.x)$ et la restreindre à divers sous-espaces stables, comme :
- le sous-espace K^(X) des applications à support fini, dont la base canonique (δ_x)_x∊X (où δ désigne le symbole de Kronecker : δ_x(y) vaut 1 pour y=x et vaut 0 pour les autres y∊X) est permutée par chaque élément du groupe : ρ(g)(δ_x)=δ_gx. Pour l'action à gauche de G sur lui-même, la représentation correspondante de G sur K^(G) est appelée la représentation régulière gauche de G.
- le sous-espace des fonctions continues sur X, si G est un groupe topologique et X un espace topologique et si l'action est continue ou même si on a seulement, pour tout g∊G, continuité de l'application X→X, x↦g.x.

Glossaire des représentations

Comme toute action de groupe, la représentation est dite fidèle si le morphisme ρ est injectif. Cette notion est différente de celle de module fidèle : le K-espace vectoriel de la représentation étant un module sur l'algèbre K[G] du groupe G (cf. infra), si ce module est fidèle alors la représentation de G est fidèle, mais la réciproque est fausse.
La représentation est dite matricielle si l'espace V est de la forme Kⁿ pour un certain entier naturel n, auquel cas le groupe (GL_n(V),∘) s'identifie canoniquement au groupe GL_n(K) des matrices carrées d'ordre n à coefficients dans K inversibles (autrement dit : de déterminant non nul), muni du produit matriciel. Via cette identification, deux représentations matricielles R et S sont donc équivalentes si et seulement s'il existe une matrice inversible P telle que pour tout élément g de G, R_g=P ^-1.S_g.P.
La dimension de V est appelée degré de la représentation. Si V est de dimension finie n (ce que l'on suppose toujours implicitement dans la théorie des représentations d'un groupe fini), la représentation est équivalente à une représentation matricielle, via le choix arbitraire d'un isomorphisme φ de Kⁿ dans V.

Détails

Soit (e_i)_i=1,...,n l'image par φ de la base canonique de Kⁿ. La donnée de cette base de V permet d'associer à chaque endomorphisme a de V une matrice carrée d'ordre n, dont les coefficients a_ij sont les éléments de K donnés par les égalités suivantes :

\forall j \in [\![1;n]\!] \quad a(e_j)=\sum_{i=1}^n a_{i,j}\cdot e_i

L'application qui à un endomorphisme a associe la matrice définie précédemment est un isomorphisme d'anneaux, de l'anneau L(V) des endomorphismes de V dans celui, M_n(K), des matrices carrées d'ordre n à coefficients dans K. Ce morphisme induit un isomorphisme de groupes entre les groupes des inversibles de ces deux anneaux : les groupes GL(V) et GL_n(K). Par composition avec cet isomorphisme de groupes, toute représentation de G sur V est équivalente à une représentation matricielle, avec φ pour isomorphisme d'entrelacement.

Une sous-représentation de (V, ρ) est la représentation (W,σ) obtenue par restriction à un sous-espace vectoriel W stable sous l'action de G.

Détails

On suppose que pour tout élément g de G, W est stable par ρ(g). On peut alors définir chaque endomorphisme σ(g) de W comme la restriction de ρ(g) à W. Les σ(g) vérifient σ(g₁)∘σ(g₂)=σ(g₁g₂) et l'image par σ de l'élément neutre de G est la restriction à W de l'identité de V, donc c'est l'identité de W, qui est bien un automorphisme de W. Les conditions suffisantes sont remplies pour que σ soit une représentation de G sur W.

Une représentation de degré non nul est dite irréductible si elle n'admet pas d'autre sous-représentation qu'elle-même et la représentation de degré nul, autrement dit si V n'a pas de sous-espace propre stable par l'action de G. En termes matriciels, cela signifie qu'on ne peut pas trouver de base dans laquelle la représentation de G soit donnée par des matrices ayant toutes la même structure triangulaire supérieure par blocs (avec au moins deux blocs diagonaux).
La somme directe d'une famille de représentations (V_i, ρ_i) de G est la représentation ρ sur l'espace vectoriel somme directe des V_i définie par : ρ(g) = ⊕_i ρ_i(g). En termes matriciels, cela signifie qu'en juxtaposant des bases des V_i pour former une base de leur somme directe, la représentation ρ est faite par des matrices diagonales par blocs, chaque bloc correspondant à l'une des représentations ρ_i.
Une représentation est dite complètement réductible si elle est somme directe de représentations irréductibles.
Deux représentations sont dites disjointes si elles n'ont aucune composante irréductible commune, ou encore s'il n'existe aucun morphisme non nul entre elles.
Si V est un espace de Hilbert dont le produit scalaire est invariant sous l'action de G, on dit que la représentation est unitaire (en).
Si G est un groupe topologique et V un espace vectoriel topologique, la représentation ρ est une représentation continue si l'application G × V → V, (g, v) ↦ g.v est continue.

Lien avec les K[G]-modules

La K-algèbre de G, notée K[G] et constituée des combinaisons linéaires finies formelles d'éléments de G à coefficients dans K, est une K-algèbre associative dont la multiplication étend naturellement la loi du groupe G.

On peut alors étendre, et ce de façon unique, la représentation 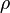$\rho$ en un morphisme de K-algèbres de K[G] vers End(V), en posant

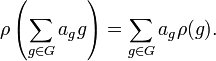
\rho\left(\sum_{g\in G}a_gg\right)=\sum_{g\in G}a_g\rho(g).

Ceci fait de V un K[G]-module. On dit également que V est un G-module (en).

Réciproquement, la donnée d'un K[G]-module fournit une représentation de G.

Via ce « dictionnaire » :

un morphisme de représentations correspond à un morphisme de K[G]-modules ;
la représentation régulière (cf section « Exemples » ci-dessus) correspond à la structure naturelle de K[G] vu comme module à gauche sur lui-même ;
une représentation 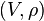$(V,\rho)$ est irréductible si et seulement si V est simple en tant que K[G]-module ;
elle est complètement réductible si et seulement si V est semi-simple.

Irréductibilité

Le fait de considérer des représentations irréductibles permet de beaucoup simplifier certains raisonnements : par exemple, d'après le lemme de Schur, un morphisme entre deux modules simples est soit nul, soit inversible.

On peut souvent ramener l'étude des représentations de G à l'étude de ses représentations irréductibles : si V n'est pas irréductible, on peut toujours considérer un sous-espace vectoriel de V qui soit stable par G. Si jamais V est de dimension finie, on pourra ainsi finir par trouver un sous-module simple.

Théorème de Maschke — Si G est un groupe fini et si la caractéristique de K ne divise pas card(G), alors tout K[G]-module est semi-simple (ou de façon équivalente : toute représentation de G sur un K-espace vectoriel est complètement réductible).

Ce théorème se généralise partiellement aux représentations continues de groupes compacts.

Si G est un groupe fini, toute représentation irréductible complexe (de degré fini) de G est équivalente à une sous-représentation de la représentation régulière.

Référence

Jean-Pierre Serre, Représentations linéaires des groupes finis [détail des éditions]

Articles connexes

Théorie des représentations
Représentation d'algèbre (en)
Représentation d'algèbre de Lie
Représentation d'un groupe de Lie

Portail de l’algèbre

This article is issued from Wikipédia - version of the Saturday, December 13, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.