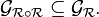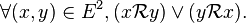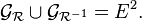Relation binaire
En mathématiques, une relation binaire entre deux ensembles E et F (ou simplement relation entre E et F) est caractérisée par un sous-ensemble du produit cartésien E × F, soit une collection de couples dont la première composante est dans E et la seconde dans F. Cette collection est désignée par le graphe de la relation. Les composantes d'un couple appartenant au graphe d'une relation R sont dits en relation par R. Une telle relation binaire est parfois appelée correspondance entre les deux ensembles.
Par exemple, en géométrie plane, la relation d'incidence entre un point et une droite du plan « le point A est sur la droite d » est une relation binaire entre l'ensemble des points et l'ensemble des droites du plan. Les fonctions ou applications d'un ensemble E dans un ensemble F peuvent être vues comme des cas particuliers de relations binaires entre E et F.
Lorsque F = E, l'ordre des deux composantes d'un couple a son importance. Par exemple, la relation « … est strictement inférieur à … », notée <, sur l'ensemble N des entiers naturels est une relation sur N ; on note n < p pour indiquer que n et p sont en relation. Le couple (1, 2) est un élément du graphe, contrairement au couple (2, 1).
La notion de relation peut être généralisée à plus de deux arguments, voir relation (mathématiques).
Introduction
De manière informelle, une relation entre deux ensembles est une proposition qui lie certains éléments du premier ensemble avec d'autres éléments du second ensemble.
Sur un ensemble F constitué de filles et un ensemble G constitué de garçons, par exemple, on pourrait définir une relation « Alice aime Bernard », ou une autre relation « Béatrice connaît Paul »… On peut donc voir la relation comme étant des fils reliant des éléments de deux ensembles.
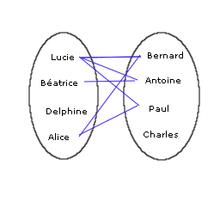
Dans le cas d'un ensemble fini, on peut alors tenter de représenter la relation par un diagramme. Si F = {Lucie, Béatrice, Delphine, Alice} et si G = {Bernard, Antoine, Paul, Charles}, la relation aime peut être schématisée par le diagramme joint (un tel diagramme est dit diagramme sagittal).
On peut également représenter cette relation, par un tableau à deux entrées, avec en première colonne la liste des éléments de l'ensemble de départ F, et en première ligne celle des éléments de l'ensemble d'arrivée G. Les couples sont représentés par des croix dans les cases à l'intersection de la ligne de la première composante et de la colonne de la seconde composante.
| . | Bernard | Antoine | Paul | Charles |
|---|---|---|---|---|
| Lucie | X | X | X | . |
| Béatrice | . | X | . | . |
| Delphine | . | . | . | . |
| Alice | X | . | X | . |
On pourra déplorer le fait que Delphine n'aime personne, que Lucie ait un cœur généreux et que Charles puisse se sentir seul.
On peut aussi tenter de faire la liste des couples ainsi en relation (pour plus de commodité, on ne conservera que les deux premières lettres du prénom) :
- Gr = {(Lu,Be) , (Lu, An) , (Lu, Pa) , (Bé, An) , (Al, Pa) , (Al, Be)}
En mathématiques, un « couple » est formé de deux éléments mis entre parenthèses dans un ordre particulier. La relation est définie comme un ensemble de couples, c'est-à-dire que si deux éléments sont reliés entre eux, alors le couple est un élément de l'ensemble relation. Si l'on appelle F l'ensemble des filles, et G l'ensemble des garçons, alors l'ensemble de tous les couples possibles est appelé « produit cartésien de F par G » et est noté F × G et la relation aime est alors définie par l'ensemble F, l'ensemble G et un sous-ensemble de F × G.
Définition formelle
Une relation binaire R d'un ensemble E vers un ensemble F est définie par une partie G de E × F.
Si (x,y) ∈ G, on dit que x est en relation avec y et l'on note « x R y » (notation infixe), « R(x, y) », « R x y » (notations préfixes).
On remarquera qu'il est nécessaire, pour une relation binaire, de préciser l'ensemble E (appelé ensemble de départ), l'ensemble F (appelé ensemble d'arrivée) et la partie G de E × F appelée le graphe de la relation.
L'ensemble de définition est l'image de G par la première projection, c'est-à-dire le sous-ensemble suivant de l'ensemble de départ :
 Une relation binaire peut aussi être vue comme une « fonction multivaluée », également appelée « correspondance », et le vocabulaire dans ce contexte désigne les mêmes notions (en particulier : graphe, ensemble de définition, image, réciproque)[1].
Une relation binaire peut aussi être vue comme une « fonction multivaluée », également appelée « correspondance », et le vocabulaire dans ce contexte désigne les mêmes notions (en particulier : graphe, ensemble de définition, image, réciproque)[1].
Composition et réciproque
Composition
Si 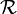 est une relation de E dans F et
est une relation de E dans F et 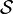 de F dans G, on peut définir une relation
de F dans G, on peut définir une relation 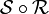 de E dans G par :
de E dans G par :
Plus simplement, on peut dire que  est défini par la règle qui dit que
est défini par la règle qui dit que 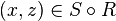 si et seulement s'il existe un élément
si et seulement s'il existe un élément 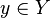 tel que
tel que 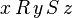 (i.e.
(i.e. 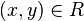 et
et  ).
).
Notation : si 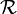 est une relation sur un ensemble E et n un entier naturel, on note
est une relation sur un ensemble E et n un entier naturel, on note 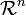 la composition de
la composition de 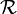 avec elle-même n fois, avec la convention que
avec elle-même n fois, avec la convention que  dénote la relation d'égalité sur E.
dénote la relation d'égalité sur E.
Réciproque
Si 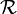 est une relation de E sur F, on peut définir une relation de F sur E dite relation inverse, ou réciproque, par :
est une relation de E sur F, on peut définir une relation de F sur E dite relation inverse, ou réciproque, par :
 .
.
Exemples :
- « plus petit que » et « plus grand que » sont des relations réciproques l'une de l'autre ;
- « aime » et « est aimé par » sont aussi réciproques l'une de l'autre.
La représentation d'une relation réciproque se déduit simplement de celle de la correspondance de départ :
- pour la représentation sagittale, en changeant le sens des liens (vu de la gauche vers la droite sur le schéma) ;
- pour une représentation matricielle, en échangeant lignes et colonnes et en prenant la matrice symétrique par rapport à la diagonale principale.
Relation fonctionnelle
Lorsque, pour tout élément x de E, x n'est en relation qu'avec 0 ou 1 élément y de F, on dit que la relation est fonctionnelle. C'est une façon élémentaire de définir la notion de fonction. En langage formel, la propriété précédente s'écrit :
Exemple important :
- La diagonale de E est définie par :
-
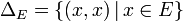 .
.
-
- C'est le graphe de la relation d'égalité sur E, notée =E, ou = en l'absence d'ambiguïté sur l'ensemble concerné.
- Cette relation est aussi une fonction, l'identité de E, notée idE.
Relation sur (ou dans) un ensemble
Dans le cas particulier où E = F, on dit que R est une relation binaire définie sur E ou dans E.
Propriétés liées à la réflexivité
Relation réflexive
La relation 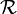 sur E est réflexive si tout élément de E est en relation avec lui-même, c'est-à-dire si :
sur E est réflexive si tout élément de E est en relation avec lui-même, c'est-à-dire si :
Une relation est donc réflexive si et seulement si son graphe contient la diagonale de E, c'est-à-dire si et seulement si :
Exemples :
- la relation d'inclusion entre ensembles est réflexive : tout ensemble est inclus dans lui-même ;
- dans un ensemble de nombres, la relation « est un diviseur de » est réflexive : tout nombre est son propre diviseur ;
- dans un ensemble de personnes, la relation « est de la même famille que » est réflexive.
La clôture réflexive, notée  , d'une relation
, d'une relation 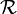 sur un ensemble E est la relation sur E dont le graphe est l'union de celui de
sur un ensemble E est la relation sur E dont le graphe est l'union de celui de 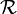 et de la diagonale de E :
et de la diagonale de E :
Relation irréflexive
La relation 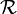 sur E est irréflexive ou antiréflexive si aucun élément de E n'est en relation avec lui-même, c'est-à-dire si :
sur E est irréflexive ou antiréflexive si aucun élément de E n'est en relation avec lui-même, c'est-à-dire si :
Une relation est donc irréflexive ou antiréflexive si et seulement si son graphe est disjoint de la diagonale de E, c'est-à-dire si :
Exemples :
- l'inégalité stricte sur les entiers relatifs est un exemple de relation irréflexive : aucun entier n'est strictement inférieur à lui-même ;
- dans un ensemble de personnes, la relation « est enfant de » est irréflexive : personne n'est son propre enfant ;
- dans un polyèdre, la relation « a un et un seul côté commun avec » est une relation irréflexive entre ses faces : aucune face n'a qu'un seul côté commun avec elle-même (une face a au moins 3 côtés en commun avec elle-même).
Une relation sur un ensemble d'au moins deux éléments peut n'être ni réflexive, ni irréflexive : il suffit qu'un élément soit en relation avec lui-même et l'autre non.
Propriétés liées à la symétrie
Relation symétrique
La relation 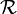 sur E est symétrique si et seulement si lorsqu'un premier élément de E est en relation avec un second élément de E, le second élément est lui aussi en relation avec le premier, c'est-à-dire si :
sur E est symétrique si et seulement si lorsqu'un premier élément de E est en relation avec un second élément de E, le second élément est lui aussi en relation avec le premier, c'est-à-dire si :
Une relation est donc symétrique si et seulement si son graphe se confond avec celui de sa relation inverse, c'est-à-dire si :
En d'autres termes, une relation symétrique est une relation égale à sa réciproque :
L'égalité entre graphes ci-dessus peut encore s'écrire :
Exemples :
- dans un ensemble de personnes, la relation « est de la même famille que » est symétrique ;
- dans un polyèdre, la relation « a un et un seul côté commun avec » est une relation symétrique entre ses faces : si une face a un côté commun avec une autre face, cette dernière a le même côté commun avec la première face ;
- parmi les entiers naturels, la relation « forme un produit pair avec » est symétrique, car la multiplication des entiers est commutative.
La clôture symétrique, notée  , d'une relation
, d'une relation 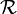 sur un ensemble E est la relation sur E dont le graphe est l'union de celui de
sur un ensemble E est la relation sur E dont le graphe est l'union de celui de 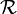 et de sa réciproque (ou inverse) :
et de sa réciproque (ou inverse) :
Cette clôture symétrique est d'ailleurs « universelle » parmi les relations symétriques contenant 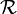 (ce qui ici, sans entrer dans des considérations catégoriques, signifie que c'est « la plus petite »).
(ce qui ici, sans entrer dans des considérations catégoriques, signifie que c'est « la plus petite »).
Relation antisymétrique
On distingue en français deux sortes d'antisymétrie de relation, l'antisymétrie faible et l'antisymétrie forte ou asymétrie.
La relation 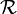 sur E est dite antisymétrique ou faiblement antisymétrique si lorsque deux éléments de E sont en relation mutuelle, ils sont en fait confondus, c'est-à-dire si :
sur E est dite antisymétrique ou faiblement antisymétrique si lorsque deux éléments de E sont en relation mutuelle, ils sont en fait confondus, c'est-à-dire si :
Une relation est donc faiblement antisymétrique si et seulement si l'intersection de son graphe avec celui de sa réciproque est incluse dans la diagonale de E, c'est-à-dire si :
Exemples :
- la relation « plus grand que (ou égal à) » ainsi que la relation « plus petit que (ou égal à) » sur les entiers naturels ou sur les réels ;
- la relation « divise » dans l'ensemble des entiers naturels.
Quand une relation est à la fois antisymétrique et irréflexive, on dit parfois qu'elle est fortement antisymétrique (on lit asymétrique dans certains ouvrages). On peut alors simplifier la définition : la relation 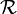 sur E est fortement antisymétrique si et seulement si lorsqu'un premier élément de E est en relation avec un second élément de E, le second élément n'est pas en relation avec le premier, autrement dit :
sur E est fortement antisymétrique si et seulement si lorsqu'un premier élément de E est en relation avec un second élément de E, le second élément n'est pas en relation avec le premier, autrement dit :
Une relation est donc fortement antisymétrique si et seulement si l'intersection de son graphe est disjoint de celui de sa réciproque, c'est-à-dire si :
Exemples :
- les relations d'ordre strict, comme la relation « est strictement plus grand que » sur les entiers ou les réels, ou la relation d'inclusion stricte sont fortement antisymétriques.
- dans un ensemble de personnes, la relation « est enfant de » est asymétrique : personne n'est son propre enfant, ni a fortiori l'enfant de ses enfants…
Propriétés :
- Si une relation est irréflexive, l'antisymétrie forte et l'antisymétrie faible sont équivalentes, et donc la plupart du temps on parle simplement d'antisymétrie.
- Toute relation à la fois symétrique et fortement antisymétrique (i.e. asymétrique) est une relation vide, c'est-à-dire que son graphe est l'ensemble vide (autrement dit, il n'existe aucun élément x de l'ensemble E qui soit relié à un autre élément y de E par cette relation).
- Par contre une relation qui décrit l'égalité sur un ensemble quelconque E est à la fois symétrique et antisymétrique.
- Une relation peut n'être ni symétrique ni antisymétrique, comme la relation de divisibilité sur les entiers relatifs.
Transitivité
La relation 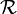 sur E est transitive si lorsqu'un premier élément de E est en relation avec un deuxième élément lui-même en relation avec un troisième, le premier élément est aussi en relation avec le troisième, c'est-à-dire si :
sur E est transitive si lorsqu'un premier élément de E est en relation avec un deuxième élément lui-même en relation avec un troisième, le premier élément est aussi en relation avec le troisième, c'est-à-dire si :
Une relation 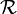 est donc transitive si et seulement si son graphe contient celui de sa composée avec elle-même, c'est-à-dire si :
est donc transitive si et seulement si son graphe contient celui de sa composée avec elle-même, c'est-à-dire si :
Exemple : la relation ≤ sur les entiers naturels est transitive.
On appelle clôture transitive, ou fermeture transitive de 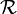 la relation
la relation
Elle est « universelle » parmi les relations transitives contenant 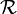 . Elle est notée
. Elle est notée 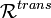 .
.
Relation totale
La relation 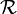 sur E est totale si pour toute paire d'éléments de E, elle institue au moins un lien entre les deux éléments considérés, c'est-à-dire si :
sur E est totale si pour toute paire d'éléments de E, elle institue au moins un lien entre les deux éléments considérés, c'est-à-dire si :
La relation est donc totale si et seulement si l'union de son graphe avec celui de sa réciproque est égale au carré cartésien de E, c'est-à-dire si :
Exemple : la relation ≤ sur l'ensemble des réels est totale.
Contre-exemple : la relation « divise » sur l'ensemble des entiers naturels n'est pas totale.
Relation d'équivalence
Une relation d'équivalence est une relation réflexive, transitive et symétrique. L'exemple le plus simple de relation d'équivalence est l'égalité. En arithmétique, la relation de congruence modulo un entier donné est une relation d'équivalence.
Relation d’ordre
Une relation d'ordre est une relation réflexive, transitive et antisymétrique.
Si la relation est totale alors on dit que l'ordre est total. C'est le cas de la relation « est inférieur ou égal à » sur les entiers naturels ou sur les réels. Tous les éléments ne sont pas forcément comparables par une relation d'ordre ; par exemple deux entiers naturels ne sont pas forcément comparables par divisibilité. On dit alors que la relation « est un diviseur de » est un ordre partiel sur N.
Relation bien fondée
Exemples
- La relation d'appartenance sur E × P(E), où P(E) désigne l'ensemble des parties de E ;
- la relation d'inclusion sur P(E) (relation d'ordre).
Nombre de relations binaires sur des ensembles finis
Considérons un ensemble E fini de cardinal n et un ensemble F fini de cardinal p. Il y a autant de relations binaires de E sur F que d'applications de E × F dans {0, 1}, ce qui donne 2np relations.
En particulier, si E = F, on trouve 2(n2) relations binaires sur E, dont
- 2n(n – 1) relations réflexives,
- 2n(n + 1)/2 relations symétriques.
- Pour le nombre de relations transitives, il n'y a toujours pas actuellement de formule « fermée ».
Le nombre de relations d'équivalence est égal au nombre de partitions d'un ensemble, c'est-à-dire le nombre de Bell.
Notes et références
- ↑ Dany-Jack Mercier, Acquisition des fondamentaux pour les concours, vol. 1, Publibook, (lire en ligne), p. 104.
- N. Bourbaki, Éléments de mathématique : Théorie des ensembles [détail des éditions]
- Paul Halmos, Introduction à la théorie des ensembles [détail des éditions]
- (en) Yiannis Moschovakis (de), Notes on Set Theory [détail des éditions]
Articles connexes
- Fonction multivaluée (même concept que la relation binaire mais avec généralement de la structure supplémentaire sur les ensembles
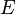 et
et 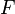 ).
). - Opération sur des correspondances
- Théorie des graphes
- Portail des mathématiques


![\forall x \in E, \forall y \in F, \forall z \in F , [ ( x , y ) \in \mathcal{G}_{\mathcal{R}} \and ( x , z ) \in \mathcal{G}_{\mathcal{R}} ] \Rightarrow ( y = z ).](../i/m/11e8df4a1c2f8ccd046d7191a30efe68.png)
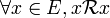
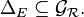


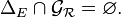
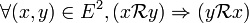
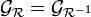
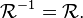
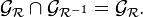
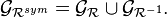
![\forall ( x , y ) \in E^2 , [ ( x \mathcal{R} y ) \wedge ( y \mathcal{R} x ) ] \Rightarrow ( x = y ).](../i/m/a0604f87b98154d95dde011602fbf713.png)
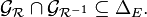
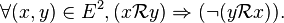
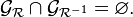
![\forall ( x , y , z ) \in E^3 , [ ( x \mathcal{R} y ) \wedge ( y \mathcal{R} z ) ] \Rightarrow ( x \mathcal{R} z ) \,](../i/m/60389ac1afdf96dab599d05d83ccf780.png)