Quantificateur (logique)
Pour les articles homonymes, voir Quantificateur.Les expressions « pour tout » et « il existe » utilisées pour formuler des propositions mathématiques dans le calcul des prédicats sont appelées des quantifications et le symbole qui les représente en langage formel est appelé un quantificateur (moins souvent un quanteur[1]) et implanté par les caractères unicode (U+2200, ∀ et U+2203, ∃)[2]'[3].
Quantification universelle
La quantification universelle (« pour tout ... » ou « quel que soit ... ») se dénote par le symbole ∀ (un A à l'envers), plus précisément,
- ∀x P(x)
et signifie
- « pour tout x P(x) (tout objet du domaine considéré possède la propriété P) ».
La notation « ∀ » a été utilisée pour la première fois[4] par Gerhard Gentzen en 1933 (publié en 1934[5]). Le mot allemand "alle" signifiant "tout", il propose un "symbole (Zeichen) valant pour tout (für alle)". Gentzen indique qu'il a choisi comme « symbole pour tout » (All-Zeichen) le « A » renversé par analogie avec le symbole « ∃ » pour le quantificateur existentiel qu'il tient de Russell.
Quantification existentielle
La quantification existentielle (« il existe un ... » au sens « il existe au moins un ... ») se note avec le signe ∃ (un E retourné). Plus précisément,
- ∃x P(x)
signifie
- il existe au moins un x tel que P(x) (un objet au moins du domaine considéré possède la propriété P)
Pour exprimer l'unicité en plus de l'existence, le signe utilisé est ∃! (le quantificateur existentiel suivi d'un point d'exclamation), plus précisément,
- ∃!x P(x)
signifie
- il existe un unique x tel que P(x), ou encore il existe un et un seul x tel que P(x) (un objet exactement du domaine considéré possède la propriété P).
Ce dernier quantificateur se définit en calcul des prédicats égalitaire à partir des deux quantificateurs précédents (et de l'égalité), par exemple par
- ∃!x P(x) ≡ ∃x [P(x) et ∀y(P(y) ⇒ y = x)].
La notation ∃ a tout d'abord été employée par Giuseppe Peano en 1897 dans le volume II de son Formulaire de mathématiques[6] avec une syntaxe différente, le signe étant directement associé au prédicat (∃ P pour notre ∃x P(x)). Bertrand Russell l'utilise le premier de la façon actuelle, comme un opérateur de liaison[4].
Négation des quantificateurs
La négation de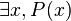 
est :
, soit :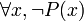 
La négation de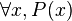 
est :
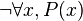, soit : 
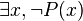en logique classique, mais pas en logique intuitionniste.
Ordre des quantificateurs
Pour une formule mise en forme prénexe l'ordre des quantificateurs entre chaque bloc de quantificateurs identiques (donc bloc de quantificateurs existentiels ou bloc de quantificateur universels) est indifférent, la formule restant la même. Par contre l'alternance des blocs de quantificateurs existentiels ou universels donne des formules bien distinctes dont la complexité logique s'observe notamment dans la hiérarchie arithmétique.
Références
- ↑ quanteur dans le dictionnaire du CNTRL.
- ↑ « Unicode Character 'FOR ALL' (U+2200) ».
- ↑ « Unicode Character 'THERE EXISTS' (U+2203) ».
- 1 2 Jeff Miller, Earliest Uses of Symbols of Set Theory and Logic, sept 2010, (Premiers usages des symboles logiques dans la théorie des ensembles).
- ↑ « Untersuchungen über das logische Schließen. I », Mathematische Zeitschrift, vol. 39 (2), , p. 176-210 (lire en ligne).
- ↑ [ G. Peano (1897), Formulaire de mathématiques volume II, N°1, p 47 https://ia700307.us.archive.org/5/items/formulairedemat02peangoog/formulairedemat02peangoog.pdf].
Voir aussi
- Théorie de la description définie de Bertrand Russell
- Théorie des mondes possibles
- Notation (mathématiques)
- La lettre λ du Lambda-calcul qui elle aussi lie des variables.
Portail des mathématiques