Onde gravitationnelle

En physique, les ondes gravitationnelles sont des oscillations de la courbure de l'espace-temps. Albert Einstein en a prédit l'existence en 1918 en se basant sur sa théorie de la relativité générale[1]. Les ondes électromagnétiques (perturbations des champs électrique et magnétique) sont produites par les particules chargées accélérées. De la même façon, les ondes gravitationnelles sont produites par des masses accélérées[2]. La production efficace d'ondes gravitationnelles demande de très grandes masses et de très grandes accélérations. Ainsi, les sources d'ondes gravitationnelles sont principalement des systèmes astrophysiques impliquant des objets massifs et très denses comme les étoiles à neutrons ou les trous noirs pouvant supporter de telles accélérations.
Russell Hulse et Joseph Taylor ont fourni une preuve indirecte de l'existence de telles ondes en observant le pulsar binaire PSR B1913+16 et montrant que sa période orbitale décroît précisément comme le prédit la théorie de la relativité générale si l'on considère que ce système perd son énergie par émission gravitationnelle. Ce résultat a valu à ces deux chercheurs américains de recevoir le prix Nobel de Physique en 1993.
Introduction
Dans la théorie de la relativité générale, la gravité provient de la courbure de l'espace-temps. Cette courbure est causée par la présence d'objets possédant une masse. Plus la masse de l'objet est grande, plus la courbure produite est grande et ainsi plus la gravité est intense. Lorsque des objets massifs se déplacent dans l'espace-temps, la courbure de l'espace-temps s'ajuste pour refléter le changement de la position de ces objets. Sous certaines circonstances, les objets accélérés peuvent produire une perturbation de l'espace-temps qui s'étend et se propage de manière analogue à « des vagues à la surface de l'eau ». On désigne par onde gravitationnelle ce type de perturbation. On prédit qu'elles se propagent à la vitesse de la lumière. Ainsi, l'existence des ondes gravitationnelles résulte en quelque sorte de l'application à la gravité du principe d'invariance de Lorentz qui introduit le concept de vitesse limite pour la propagation des interactions physiques (concept inexistant dans la vision newtonienne de la gravitation, cette interaction se propageant à une vitesse infinie dans cette théorie).
L'analogie entre des charges électriques en mouvement et des masses en mouvement permet de mieux appréhender le phénomène : de la même manière que l'accélération de particules chargées produit des ondes électromagnétiques, l'accélération de particules possédant une masse produit des ondes gravitationnelles. La plupart des théories de gravité quantique postulent l'existence d'un quantum correspondant appelé le graviton de façon analogue à l'électrodynamique quantique dans laquelle le vecteur de la force électromagnétique n'est autre que le photon. L'onde gravitationnelle est associée au graviton et ses caractéristiques donnent alors de précieuses informations sur cette particule.
Effet causé
 Effet sur un cercle de masse en chute libre de la polarisation « plus » d'une onde gravitationnelle. |
 Effet sur un cercle de masse en chute libre de la polarisation « croix » d'une onde gravitationnelle. |
Considérons un cercle de particules test en chute libre (soumises uniquement à la gravité). Les ondes gravitationnelles étant « transverses », leur effet sur les particules est nul dans la direction de propagation. Par contre, une onde gravitationnelle qui se propage perpendiculairement au plan du cercle entraîne la déformation de ce cercle. Il est étiré de manière alternée dans une direction tandis qu'il est comprimé dans l'autre tout en gardant une surface constante comme indiqué dans les animations ci-contre. L'amplitude des oscillations montrées dans les animations est grandement exagérée. En réalité, l'amplitude des ondes gravitationnelles est très petite.
Les animations nous permettent de visualiser les oscillations associées à une onde gravitationnelle sinusoïdale ce qui explique l'évolution des figures dans les animations. Une telle onde peut être produite par le système physique idéal constitué d'une paire de masses identiques en orbite circulaire. Dans ce cas, l'amplitude de l'onde est constante et son plan de polarisation tourne continûment à deux fois la fréquence orbitale.
On note usuellement l'amplitude des ondes gravitationnelles 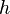 , qui est un nombre sans dimension, quantifiant l'importance relative de la compression ou de l'étirement dans les animations. L'amplitude montrée ici est d'environ
, qui est un nombre sans dimension, quantifiant l'importance relative de la compression ou de l'étirement dans les animations. L'amplitude montrée ici est d'environ  (soit 50 %). Dans la réalité, les ondes gravitationnelles reçues sur Terre sont imperceptibles : typiquement, on estime que
(soit 50 %). Dans la réalité, les ondes gravitationnelles reçues sur Terre sont imperceptibles : typiquement, on estime que 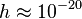 , c'est-à-dire qu'un cercle de la taille de la Terre subirait une déformation
, c'est-à-dire qu'un cercle de la taille de la Terre subirait une déformation  m, mille fois plus petite qu'un atome.
m, mille fois plus petite qu'un atome.
Polarisation
Il existe deux polarisations, ce qui est équivalent à dire que les ondes gravitationnelles possèdent deux degrés de liberté indépendants notés 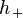 et
et 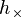 .
.
La polarisation d'une onde gravitationnelle est identique à celle d'une onde lumineuse à ceci près que l'angle entre les polarisations est de 45 degrés au lieu de 90 degrés. L'effet d'une onde rectilignement polarisée avec la polarisation « plus » est identique à celui avec la polarisation « croix » mais tourné de 45 degrés comme illustré dans les animations ci-dessus. La polarisation des ondes gravitationnelles résulte de la nature de leur source et le degré de polarisation dépend de l'orientation de la source par rapport à l'observateur. Les ondes gravitationnelles sont définies comme les perturbations de la métrique qui du point de vue des équations d'Einstein sont découplées des perturbations du tenseur énergie-impulsion. Les ondes gravitationnelles ont une symétrie tensorielle (mathématiquement, on parle de spin 2), par opposition aux perturbations de la matière qui ont soit une symétrie scalaire (spin 0), soit une symétrie vectorielle (spin 1). Ceci est directement relié au nombre de polarisations.
Pour trouver l'origine de ce nombre, il faut considérer le tenseur métrique dans son ensemble, qui est décrit par une matrice symétrique contenant 10 entrées indépendantes, et soustraire tout d'abord les degrés de liberté non-physiques associés à l'invariance de la théorie sous la symétrie de reparamétrisation de l'espace-temps. Ceux-ci sont au nombre de 4. Il faut également soustraire les degrés de liberté qui sont couplés aux perturbations du tenseur énergie-impulsion. Il y a un tel degré scalaire et trois degrés vectoriels. Finalement, il ne reste donc que deux degrés de propagation physique[Note 1].
Existence
L'existence des ondes gravitationnelles a été longuement débattue[3]. La question était de savoir si ces ondes avaient effectivement une réalité physique ou bien résultaient d'un « pur effet de jauge », autrement dit d'un choix de système de coordonnées. Cette question a été définitivement tranchée lors de la conférence de Chapel Hill (États-Unis) en 1957[4]. Les contributions de Felix Pirani et Hermann Bondi ont été déterminantes. Pirani montre qu'en présence d'une onde gravitationnelle, un ensemble de masses en chute libre est alors animé d'un véritable mouvement l'une par rapport à l'autre (tel qu'illustré plus haut). Bondi suggère qu'en connectant deux masses aux extrémités d'un piston, on absorbe alors l'énergie de l'onde en la transformant en chaleur (« sticky bead » argument), ce qui démontre que l'onde possède bien une réalité physique. Ce fut le point de départ des premiers développements d'instruments permettant la mise en évidence expérimentale des ondes gravitationnelles.
Sources
Amplitude des ondes gravitationnelles émises par un système physique
La formule du quadrupôle obtenue par Albert Einstein en 1916 permet de relier
l'amplitude de l'onde émise par un système physique à la variation de son moment quadrupolaire 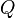 :
:
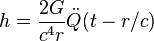
Pour un système continue doté d'une densité volumique de masse 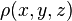 , celui-ci est
[5]
, celui-ci est
[5]
 où les indices
où les indices 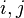 correspondent aux coordonnées cartésiennes
correspondent aux coordonnées cartésiennes 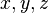 et
et  est le symbôle de Kronecker.
est le symbôle de Kronecker.
La petitesse du facteur 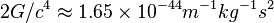 traduit la grande rigidité de l'espace-temps. Il faut la compenser par de grandes variations du moment quadrupôlaire pour produire des ondes gravitationnelles détectables.
traduit la grande rigidité de l'espace-temps. Il faut la compenser par de grandes variations du moment quadrupôlaire pour produire des ondes gravitationnelles détectables.
Ceci a plusieurs conséquences importantes. Les systèmes dont la dynamique est à symétrie sphérique (sphère en expansion ou en contraction) ou à symétrie cylindrique (disque en rotation sur son axe) n'émettent pas d'ondes gravitationnelles puisque leur moment quadrupolaire reste constant.
Un dispositif simple pour la production d'onde gravitationnelle est un haltère en rotation autour
du centre de son axe. Un tel système avec deux masses m séparées d'une distance R en rotation à la vitesse angulaire 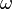 donne
donne  . Cette estimation, appliquée à des systèmes aux dimensions réalistes pour une expérience construite par l'homme, montre que la production d'ondes gravitationnelles détectables est impraticable en laboratoire.
. Cette estimation, appliquée à des systèmes aux dimensions réalistes pour une expérience construite par l'homme, montre que la production d'ondes gravitationnelles détectables est impraticable en laboratoire.
C'est pourquoi l'on s'intéresse à des sources astrophysiques, qui font généralement intervenir des objects compacts (comme les étoiles à neutrons et les trous noirs) présentant de grandes masses et capables de soutenir de très grandes accélérations.
Binaires compactes coalescentes

Les systèmes binaires d'étoiles à neutrons et/ou trous noirs proches de la coalescence sont l'équivalent astrophysique de l'haltère en rotation mentionné plus haut. Les deux objets composant le système orbitent l’un autour de l’autre. Le système perd de l'énergie par rayonnement gravitationnel ce qui cause le rapprochement des deux objets jusqu’à la coalescence. La fréquence orbitale augmente au fur et à mesure que le rayon orbital diminue. Ceci conduit à l'émission d'un signal gravitationnel caractéristique comme illustré ci-contre.
Fond stochastique
On distingue le fond stochastique d'onde gravitationnelle d’origine astrophysique dû à la superposition des signaux provenant d'un grand nombre de sources irrésolues (qu'il est impossible de détecter séparément) et celui d'origine cosmologique produit lors des premiers instants de l’Univers peu de temps après le Big Bang. L'observation de ce rayonnement nous donnerait des informations importantes sur l'Univers primordial, en particulier sur la période dite d'inflation cosmique[6].
Sources continues
Si elles possèdent un certain degré de non-axisymétrie, les étoiles à neutrons émettent une onde gravitationnelle monochromatique à la fréquence double de la fréquence de rotation de l’étoile. L'émission étant permanente constante en fréquence et amplitude, on peut alors « intégrer » le signal pendant plusieurs mois afin de le distinguer du bruit instrumental.
Détection
Observations indirectes
Décroissance orbitale des pulsars binaires
L'observation du pulsar binaire PSR B1913+16, découvert en 1974, a permis aux physiciens Russell Hulse et Joseph Taylor de mettre en évidence l'existence des ondes gravitationnelles. Il s'agit d'un système binaire composé de deux étoiles à neutrons. L'une des deux étoiles est un pulsar. L'observation des impulsions radio émises par celle-ci permet d'obtenir l'évolution de la période orbitale du système. Il a été observé que celle-ci se réduisait avec le temps, impliquant que le système perdait de l'énergie. Le rythme de la perte d'énergie est compatible avec l'hypothèse que le système perd son énergie par rayonnement gravitationnel conformément aux prédictions de la relativité générale. Russell Hulse et Joseph Taylor ont été récompensés par le prix Nobel de physique en 1993 pour cette découverte.
Polarisation et mode B du fond diffus micro-onde cosmologique
En mars 2014, des chercheurs du Centre d'astrophysique Harvard-Smithsonian annoncent la détection des ondes gravitationnelles produites lors de l'inflation cosmique grâce à la mesure de la polarisation du fond diffus cosmologique par le télescope BICEP2 (Background Imaging of Cosmic Extragalactic Polarization)[7],[8],[9],[10],[11],[12]. Cette étude est toutefois remise en cause plusieurs mois plus tard[13]. En effet, une analyse des données de BICEP2/Keck Array et du satellite Planck [14] qui utilise un modèle amélioré des émissions de la poussière galactique fournit une nouvelle limite supérieure sur la contribution à la polarisation du fond diffus micro-onde due aux ondes gravitationnelles primordiales. La conclusion est qu'il n'est plus exclu que cette contribution soit nulle (et que la polarisation observée soit presque intégralement due à la poussière galactique et aux effets de lentilles gravitationnelles).
Détection directe
Barres résonnantes
Les barres de Weber sont des instruments simples permettant de détecter l'effet d'une onde gravitationnelle. Il s'agit d'une barre rigide de métal isolée des vibrations externes. La distorsion de l'espace causée par une onde gravitationnelle incidente excite la barre à sa fréquence de résonance, perturbation ensuite amplifiée jusqu'à des niveaux détectables. Ce type de détecteur a été proposé et utilisé initialement par Joseph Weber de l'Université de Maryland. Weber a déclaré à plusieurs reprises avoir observé un excès de coïncidence entre les événements observés par deux barres identiques séparées de 2 km [15], ce qui l'a conduit à déclarer la découverte des ondes gravitationnelles en 1969 [16]. Ce résultat n'a pas été confirmé par les expériences de validation conduites ultérieurement[17].
Le principe du détecteur de Weber a été développé par la suite par plusieurs équipes. La cryogénie a été introduite afin d'atteindre une meilleure sensibilité en atténuant le bruit thermique causé par l'agitation brownienne des atomes composants la barre. On dénombre plusieurs instruments de ce type dans le monde dont certains sont encore en opération : ALLEGRO (Bâton-Rouge, États-Unis, actuellement démantelé), AURIGA (Legnaro/Padoue, Italie), Explorer (CERN, Suisse), et NAUTILUS (Rome Frascati, Italie). La géométrie sphérique, plutôt que cylindrique généralement utilisée, a été proposée pour le projet de détecteur miniGrail (Pays-Bas).
Détecteurs interférométriques terrestres

La première génération de détecteurs interférométriques d'ondes gravitationnelles comprend six instruments de grandes dimensions. Le projet américain LIGO consiste en trois instruments kilométriques situés au complexe nucléaire de Hanford WA (ce site accueille deux interféromètres dans la même enceinte) et Livingston LA. Le projet franco-italien VIRGO situé à Cascina près de Pise (Italie) possède un instrument de même classe. Le projet germano-britannique GEO600 localisé à Hanovre (Allemagne) aux dimensions plus modestes (300 mètres) vient compléter cet ensemble. Le projet japonais TAMA de taille similaire à GEO est actuellement démantelé. Malgré des différences technologiques importantes, tous ces instruments suivent le même principe[Note 2]. Tous captent la distorsion de l'espace-temps qu'exerce une onde gravitationnelle en mesurant avec une grande précision la différence de longueur 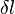 du chemin optique suivi par deux faisceaux laser se propageant dans deux directions orthogonales. En pratique on utilise l'interférométrie pour réaliser cette mesure comme indiqué sur le schéma ci-contre. Observer une variation de la différence de longueur revient à observer une variation de la différence de phase entre les deux faisceaux, et donc une variation de leur figure d'interférence.
du chemin optique suivi par deux faisceaux laser se propageant dans deux directions orthogonales. En pratique on utilise l'interférométrie pour réaliser cette mesure comme indiqué sur le schéma ci-contre. Observer une variation de la différence de longueur revient à observer une variation de la différence de phase entre les deux faisceaux, et donc une variation de leur figure d'interférence.
Le bruit de mesure (principalement le bruit thermique causé par l'agitation brownienne des atomes constituant les optiques et le bruit de photons dû à la nature quantique de la lumière) peut être réduit pour atteindre la précision de 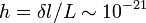 où
où 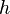 est l'amplitude de l'onde gravitationnelle et
est l'amplitude de l'onde gravitationnelle et 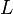 la longueur totale du chemin optique (les bras de l'interféromètre).
la longueur totale du chemin optique (les bras de l'interféromètre).
Une seconde génération de détecteurs avancés dix fois plus sensible que la première est en cours d'installation. Advanced LIGO doit effectuer une première prise de données fin 2015. Advanced Virgo devrait entrer en fonction en 2016.
Interféromètres spatiaux

Un moyen de s'affranchir du bruit sismique (terrestre) est de réaliser l'expérience dans l'espace. C'est l'objectif de la mission spatiale LISA constitué de trois satellites en formation qui réalise dans l'espace un interféromètre à 2 bras de près de 1 million de kilomètres. (Initialement, il était prévu 3 bras de 5 millions de kilomètres avant que la NASA abandonne la direction du projet LISA. C'est alors que l'ESA a pris la tête du projet et que celui-ci fut rebaptisé eLISA.) Le 28 novembre 2013, l'agence spatiale européenne a annoncé que la recherche des ondes gravitationnelles serait la thématique principale de la mission L3 avec un lancement prévu en 2034. Certaines des technologies clefs d'eLISA seront testées par le démonstrateur LISA Pathfinder (LPF)[18] qui sera lancé à l'automne 2015.
Notes et références
Notes
- ↑ À titre indicatif, la généralisation en dimension N de ce résultat aboutit à un nombre N (N -3)/ 2 de degrés de liberté pour les ondes gravitationnelles. Les ondes gravitationnelles dans des espaces à dimensions supplémentaires sont utiles dans le cadre de la cosmologie branaire.
- ↑ Idée suggérée pour la première fois dans M. E. Gertsenshtein et V. I. Pustovoit, JETP 43, 603 (1962) et dont l'applicabilité a été démontrée par R. Weiss, Electromagnetically Coupled Broadband Gravitational Antenna, Quarterly Progress Report, Research Laboratory of Electronics, MIT 105: 54 (1972).
Références
- ↑ (de) A. Einstein, 1918, Über Gravitationswellen, Sitzungsberichte der Preußischen Akademie der Wissenschaften, Berlin (Math. Phys.) p. 154-167
- ↑ (en) Michele Maggiore, Gravitational Waves -- Volume 1: Theory and Experiments, Oxford Univ. Press, 2007
- ↑ (en) D. Kennefick, Traveling at the Speed of Thought: Einstein and the Quest for Gravitational Waves. Princeton University Press (2007)
- ↑ (en) [PDF] P. Saulson, A history of Gravitational Waves, inspired by Josh Goldberg (2012) https://dcc.ligo.org/DocDB/0090/G1200429/004/Gravitational%20Waves%20and%20Josh%20Goldberg.pdf
- ↑ Weisstein, Eric, « Electric Quadrupole Moment », Eric Weisstein's World of Physics, Wolfram Research (consulté le 8 mai 2012)
- ↑ (en) S Kuroyanagi et al., Prospects for determination of thermal history after inflation with future gravitational wave detectors, Phys. Rev. D 84:123513 (2011) http://arxiv.org/abs/1110.4169
- ↑ (en) Ron Cowen, « Telescope captures view of gravitational waves », Nature,
- ↑ Big Bang : les ondes gravitationnelles d'Einstein enfin détectées.
- ↑ (en)Article plus détaillé sur BBC News
- ↑ futura-sciences.com Inflation : les ondes gravitationnelles du Big Bang enfin découvertes ?
- ↑ pourlascience.fr Ondes gravitationnelles primordiales : la preuve décisive de l'inflation cosmique se rapproche.
- ↑ Émission radio de Fance Inter (La tête au carré du 28/03/2014) : "Découverte majeure en astrophysique: les ondes gravitationnelles issues du Big Bang enfin détectées"
- ↑ The Guardian, Gravitational waves turn to dust after claims of flawed analysis
- ↑ A Joint Analysis of BICEP2/Keck Array and Planck Data
- ↑ J Weber, Gravitational-Wave-Detector Events, Phys. Rev. Lett. 20, 1307–1308 (1968) http://prl.aps.org/abstract/PRL/v20/i23/p1307_1.
- ↑ (en) J Weber Evidence for Discovery of Gravitational Radiation Phys. Rev. Lett. 22, 1320–1324 (1969) http://prl.aps.org/abstract/PRL/v22/i24/p1320_1.
- ↑ (en) H. Billing, P. Kafka, K. Maischberger, F. Meyer and W. Winkler, Results of the Munich-Frascati gravitational-wave experiment, Lettere Al Nuovo Cimento Volume 12, Number 4, 111-116, 1975. http://www.springerlink.com/content/685794h23h2222x8/.
- ↑ Page web du projet LISA Pathfinder
Voir aussi
Articles connexes
- DECIGO : Projet japonais pour tenter de détecter les ondes gravitationnelles
Liens externes
- Les ondes gravitationnelles - Astronoo
- Site du détecteur Virgo
- Site du détecteur LIGO
Bibliographie
- Pierre Binétruy, A la poursuite des ondes gravitationnelles, Collection: Quai des Sciences, Dunod 2015
- (en) Michele Maggiore, Gravitational Waves -- Volume 1: Theory and Experiments, Oxford Univ. Press (2007).
- Philippe Tourrenc, Relativité et gravitation, Armand Colin (1997).
- Portail de l’astronomie
- Portail de la cosmologie