Armure (musique)

Pour les articles homonymes, voir Armure.

Armure indiquant trois dièses à la clef (de sol) (fa

\sharp

, do

\sharp

, sol

\sharp

), c'est-à-dire une tonalité de la majeur ou de fa

\sharp

mineur.

Dans le solfège, l'armure — ou l'armature — est un ensemble d'altérations réunies à la clé. Elle est composée soit exclusivement de dièses, soit exclusivement de bémols — en dehors du cas particulier constitué par le changement d'armure. Ces altérations correspondent à la tonalité principale des mesures suivant la clé^[1].

Construction

Ces altérations, appelées altérations constitutives, dont le nombre peut varier de un à sept, se succèdent dans l'ordre du cycle des quintes :

Ordre des dièses, par quintes ascendantes : fa, do, sol, ré, la, mi, si.
Ordre des bémols, par quintes descendantes : si, mi, la, ré, sol, do, fa — soit, l'ordre inverse du précédent.

Par exemple, s'il n'y a qu'un dièse à la clé, ce sera fa $\sharp$ , s'il y en a cinq : fa $\sharp$ , do $\sharp$ , sol $\sharp$ , ré $\sharp$ et la $\sharp$ ; s'il y a deux bémols : si $\flat$ et mi $\flat$ , s'il y en a quatre : si $\flat$ , mi $\flat$ , la $\flat$ et ré $\flat$ , etc.

Effet

Alors que l'effet d'une altération accidentelle s'exerce sur toute note de même nom et de même hauteur durant la mesure où elle est placée, l'effet d'une altération constitutive est permanent : durant toute la portée, il s'exerce sur toutes les notes de même nom — même de hauteur différente — sauf bien sûr, si entre temps intervient un changement d'armure, ou plus simplement, une altération accidentelle modifiant la hauteur des notes concernées.

Exemple :

$\relative c' { \override Voice.TextScript #'staff-padding = #3 \key ees \major \override Staff.TimeSignature #'stencil = ##f \time 6/1 ees1_"1" ees'_"2" ees,_"3" e_"4" ees'_"5" e,_"6" ees'_"7" ees,_"8" }$

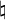Dans l'exemple ci-dessus, le mi $\flat$ (bémol constitutif) affecte toutes les notes, sauf les notes N°4 et N°6 à cause du bécarre accidentel. La note N°5, bien qu'étant également un mi $\flat$ , n'est pas affectée par le mi $\natural$ parce que située à une octave différente. Quant à la note N°8, elle n'est pas affectée puisqu'elle se situe dans une autre mesure.

Fonction

Les altérations constitutives ont pour fonction de transposer l'échelle diatonique naturelle. C'est ainsi que, quelle que soit l'armure, on trouvera toujours dans chaque octave, « deux demi-tons diatoniques isolés encadrant alternativement deux et trois tons ».

« Transposer une mélodie » signifie « déplacer cette mélodie en hauteur, sans altérer sa constitution ». Lorsqu'on transpose, les noms de notes changent, mais les intervalles entre les notes restent identiques, évitant ainsi de déformer la mélodie primitive. Si les intervalles conjoints de l'échelle diatonique étaient identiques, la transposition ne mériterait pas de longues explications. Mais comme on le sait, ces intervalles peuvent être soit des tons, soit des demi-tons diatoniques, il est donc indispensable d'avoir recours à des altérations pour que la distance exacte de ces intervalles ne soit pas modifiée au cours de la transposition.

C'est ainsi que chaque armure déterminera ses propres gammes et ses propres tonalités. Pour plus de détails sur les armures et leur signification par rapport à la tonalité d'un morceau, consulter l'article Tonalité.
Transpositions de l'échelle diatonique naturelle :

Relations entre armure, tonalité et modes majeur ou mineur

Pour connaître la tonalité d'un morceau, il faut observer son armure, c'est-à-dire le nombre d'altérations constitutives à la clef.

Pour les dièses, le dernier dièse de l'armure correspond à la note sensible, située juste un demi-ton en dessous de la tonique qui donne la tonalité du mode majeur. Par exemple, s'il y a trois dièses à la clef (fa $\sharp$ , do $\sharp$ , sol $\sharp$ ), la tonalité sera la si le mode est majeur.
Pour les bémols, l'avant dernier bémol à la clef correspond à la tonique du mode majeur. Par exemple, s'il y a deux bémols (si $\flat$ , mi $\flat$ ), la tonalité sera si $\flat$ en mode majeur.

NB : Avec un seul bémol, on est en fa majeur.

À chaque tonalité majeure est associée une tonalité en mode mineur, présentant la même armure de clef et appelée relative mineure. Pour la trouver, on descend la gamme majeure d'une tierce mineure et la note sensible est augmentée d'un demi-ton par une altération accidentelle. C'est cette altération accidentelle qui différencie le mode majeur du mode mineur.

Exemple: (do majeur) gamme: do ré mi fa sol la si do, a pour relative mineure (la mineur): la si do ré mi fa sol

\sharp

la. L'armure de clef ne comporte aucune altération.

Dans le tableau suivant sont reportées les gammes majeures ainsi que leur relatives mineures.

**Récapitulatif**
Nombre d'altérations	Tonalité	Relative mineure	note sensible: Altération accidentelle
7 $\flat$ (si,mi,la,ré,sol,do,fa)	Do $\flat$ Majeur	La $\flat$ Mineur	Sol 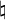$\natural$
6 $\flat$ (si,mi,la,ré,sol,do)	Sol $\flat$ Majeur	Mi $\flat$ Mineur	Ré 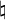$\natural$
5 $\flat$ (si,mi,la,ré,sol)	Ré $\flat$ Majeur	Si $\flat$ Mineur	La 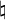$\natural$
4 $\flat$ (si,mi,la,ré)	La $\flat$ Majeur	Fa Mineur	Mi 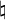$\natural$
3 $\flat$ (si,mi,la)	Mi $\flat$ Majeur	Do Mineur	Si 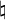$\natural$
2 $\flat$ (si,mi)	Si $\flat$ Majeur	Sol Mineur	Fa $\sharp$
1 $\flat$ (si)	Fa Majeur	Ré Mineur	Do $\sharp$
0	Do Majeur	La Mineur	Sol $\sharp$
1 $\sharp$ (fa)	Sol Majeur	Mi Mineur	Ré $\sharp$
2 $\sharp$ (fa,do)	Ré Majeur	Si Mineur	La $\sharp$
3 $\sharp$ (fa,do,sol)	La Majeur	Fa# Mineur	Mi $\sharp$
4 $\sharp$ (fa,do,sol,ré)	Mi Majeur	Do $\sharp$ Mineur	Si $\sharp$
5 $\sharp$ (fa,do,sol,ré,la)	Si Majeur	Sol $\sharp$ Mineur	Fa^x
6 $\sharp$ (fa,do,sol,ré,la,mi)	Fa $\sharp$ Majeur	Ré $\sharp$ Mineur	Do^x
7 $\sharp$ (fa,do,sol,ré,la,mi,si)	Do $\sharp$ Majeur	La $\sharp$ Mineur	Sol^x

Remarque:

Il existe une relation entre les armures des modes majeur et mineur de la même tonique. Pour obtenir l'armure de la gamme mineure, il suffit de retrancher 3 dièses (ou ajouter 3 bémols) à l'armure de la gamme majeure.

Exemples

do majeur armure vierge; do mineur armure 3

\flat

la majeur armure 3

\sharp

; la mineur armure vierge

Changement d'armure

L'armure peut être modifiée dans le cours d'un morceau, soit avec un changement de clé, soit après une double barre de mesure. Dans ce deuxième cas, l'ensemble des altérations constitutives peut inclure des bécarres. Un changement d'armure arrive par exemple à l'occasion d'une modulation.

Notes et références

↑ Claude Abromont, Guide de la théorie de la musique, Fayard, 2001 (ISBN 9782213609775), p. 530

Bibliographie

Adolphe Danhauser, Théorie de la musique : Édition revue et corrigée par Henri Rabaud, Paris, Henry Lemoine,‎ 1929, 128 p. (ISBN 979-0230922265)
Claude Abromont et Eugène de Montalembert, Guide de la théorie de la musique, Paris, Fayard,‎ 2001, 610 p. (ISBN 978-2-213-60977-5)

Voir aussi

Articles connexes

Altération (solfège)
Système tonal

Portail de la musique classique
Portail de la musique

This article is issued from Wikipédia - version of the Wednesday, October 21, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.