Approximation de Gauss

Cet article est une ébauche concernant l’optique.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

L'approximation de Gauss (d'après le physicien allemand Carl Friedrich Gauss) est l'approximation linéaire de l'optique géométrique^[1] obtenue dans certaines conditions appelées conditions de Gauss. Cette approximation, souvent applicable en pratique, permet de simplifier les relations mathématiques de l'optique géométrique. On obtient dans ces conditions un stigmatisme approché. Les écarts à cette approximation (rencontrés notamment dans les instruments d'optique travaillant en « grand angle ») sont appelés aberrations géométriques.

Conditions de Gauss

Les conditions dans lesquelles on peut appliquer l'approximation de Gauss sont les suivantes :

le système optique considéré doit être un système centré ;
les angles d'incidence des rayons sont faibles (c'est-à-dire suivant une direction proche de la normale à la surface de l'instrument d'optique) ;
le point d'incidence est proche de l'axe optique : on dit alors que l'on travaille avec des rayons paraxiaux^[2].

Lorsque ces conditions sont respectées, on peut considérer le système optique comme approximativement stigmatique. Pour réaliser ces conditions, on peut utiliser des diaphragmes qui limitent l'étendue des faisceaux autour de l'axe optique^[2].

Interprétations mathématiques

L'approximation de Gauss, appelée également approximation des petits angles, est un développement limité des fonctions trigonométriques de base pour 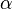$\alpha$ assez petit^[3] et exprimé en radians :

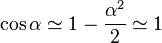$\cos \alpha \simeq 1 - \frac{\alpha^2}2\simeq 1$ ;
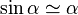$\sin \alpha \simeq \alpha$ ;
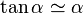$\tan \alpha \simeq \alpha$ .

Une justification rigoureuse de cette approximation est donnée, par exemple, par le théorème de Taylor (si l'on définit les fonctions trigonométriques par l'analyse), ou en partant de l'encadrement 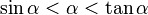$\sin \alpha<\alpha<\tan \alpha$ , qu'on peut démontrer purement géométriquement.

Notes et références

↑ José-Philippe Pérez, Optique : Fondements et applications, [détail des éditions], 5^e édition, page 28.
1 2 Optique géométrique: imagerie et instruments sur Google Livres
↑ L'erreur commise est de l'ordre de 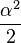$\frac {\alpha^2} 2$ pour cos, et de 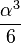$\frac {\alpha^3} 6$ pour sin ; pour des angles inférieurs à 5 degrés, soit 0,1 radians, on obtient un résultat souvent assez précis en pratique.

Voir aussi

Articles connexes

Portail de la physique
Portail de l’optique