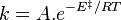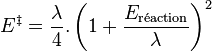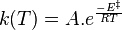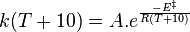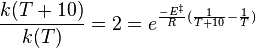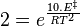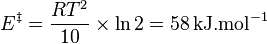Énergie d'activation

Cet article est une ébauche concernant la chimie.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

Variation de l'énergie au cours de la réaction chimique, barrière énergétique et enthalpie de réaction (exemple de la combustion du méthane dans le dioxygène)

L'énergie d'activation est une notion introduite en 1889 par le scientifique suédois Svante August Arrhenius, après avoir constaté la loi empirique qui porte son nom et qui décrit l’évolution d’une vitesse de réaction chimique avec la température. Dans sa loi (voir ci-dessous), il apparaît un terme qui possède la dimension d’une énergie molaire et qu’il appelle énergie d’activation^[1].

Le sens intuitif qui peut être donné à cette notion est une énergie qui doit être apportée à un système chimique pour que la réaction ait lieu. Cette énergie est une énergie de température.

Le sens théorique qui peut être donné à cette notion se réfère à l’équation d'Eyring qui découle d’un cadre théorique (et non de mesures empiriques). Dans la théorie d’Eyring (appelée théorie du complexe activé), l’énergie d’activation est l’enthalpie libre qui sépare l’énergie de l’état de transition et celle de l’état initial.

Cette énergie d'activation peut être diminuée, en utilisant un catalyseur.

Loi d'Arrhenius et énergie d'activation

L'expression de la loi d'Arrhenius fait apparaître l'énergie d'activation :

k = A.e^{{-E^\ddagger}/{RT}}

où :

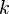$k$ , constante de vitesse de la réaction (quand elle existe) ;
$A$ , facteur préexponentiel auquel Arrhenius ne donne pas de signification ;
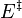$E^\ddagger$ , énergie d'activation en J·mol^-1 ;
R, constante du gaz parfait (8,31 J·mol^-1·K^-1) ;
T, température en kelvins.

Détermination de l'énergie d'activation

Approche expérimentale

Pour déterminer une énergie d'activation, il est nécessaire de déterminer la vitesse de la réaction à deux températures différentes. Le rapport des vitesses de réaction (donc des constantes de vitesses) fait disparaître le facteur préexponentiel et donne accès à 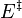$E^\ddagger$ .

Les valeurs trouvées sont toujours positives sauf dans le cas d'une réaction dont la vitesse diminuerait quand la température augmente. Trois cas existent :

les réactions enzymatiques dans la zone de température où l'enzyme se dégrade. La vitesse est alors de plus en plus lente quand la température augmente car l'enzyme est de moins en moins actif ;
certaines réactions de polymérisation qui deviennent réversibles (dépolymérisation) à haute température ;
le cas de l'oxydation de NO, qui est le seul cas de réaction en une étape. L'équation de la réaction est :

2NO(g) + O₂(g) → 2NO₂

la vitesse est v = k[NO]²[O₂]

avec :

k = 35 (en valeur relative) à 0 °C,

k = 17,6 à 100 °C,

k = 11,3 à 300 °C^[2].

Approche théorique

Il est possible de déterminer théoriquement l'énergie d'activation dans certains cas. Lors de réaction par transferts d'électrons, la théorie de Marcus permet une détermination théorique de cette grandeur. Le transfert d'électron intervient en effet dans le complexe activé à l'intersection des deux surfaces d'énergie potentielle qui décrivent l'état initial et l'état final. L'énergie d'activation est alors reliée à l'énergie de la réaction par une relation quadratique :

E^\ddagger = \dfrac{\lambda}{4} . \left( 1 + \dfrac{E_\text{réaction}}{\lambda} \right)^2

où λ est un paramètre de réorganisation qui a les dimensions d'une énergie^[3].

Conséquences

Règle pratique sur la diminution de la durée d'une réaction

Une règle pratique, en solution, est de considérer que la durée d'une réaction est diminuée de moitié quand la température est augmentée de 10 °C^[4]. Cette règle se comprend à l'aide de la loi d'Arrhenius et n'est en fait correcte que pour une certaine valeur de l'énergie d'activation qui se détermine ainsi :

k(T) = A.e^{\frac{-E^\ddagger}{RT}}

k(T+10)= A.e^{\frac{-E^\ddagger}{R(T+10)}}

\dfrac{k(T+10)}{k(T)} = 2 = e^{\frac{-E^\ddagger}{R}(\frac{1}{T+10}-\frac{1}{T})}

2 = e^{\frac{10.E^\ddagger}{RT^2}}

car T>>10, soit :

E^\ddagger = \dfrac{RT^2}{10} \times \ln 2 = 58 \, \mathrm{kJ}.\mathrm{mol}^{-1}

à 316 K.

Cela correspond effectivement à une énergie d'activation et à une température habituelles en énergie organique.

Réaction réversible

Pour une réaction réversible, l'énergie d'activation de la réaction dans le sens direct et dans le sens inverse ne sont égales que si la réaction est athermique. Dans le cas d'une réaction exothermique, l'énergie d'activation dans le sens inverse est plus grande que dans le sens direct, et inversement pour une réaction endothermique.

Voir aussi

Lien externe

http://www.universalis.fr/encyclopedie/energie-d-activation/

Références

↑ Laffitte M., Rouquerol F. (1991), La réaction chimique, tome 2 : aspects thermodynamiques (suite) et cinétiques, chap. 79, p. 211.
↑ Schuffenecker K., Scacchi G., B. Proust, Foucaut J.-F., Martel L., Bouchy M. (1991), Thermohynamique et Cinétique chimiques, Éd. Tec et doc, coll. info chimie, p. 248
↑ Sarazin J., Verdaguer M. (1991), L'oxydoréduction, concepts et expériences, Éd. Ellipse, p. 169.
↑ Sarrazin J, Verdaguer M. (1991), L'oxydoréduction, concepts et expériences, Éd. Ellipses, p. 150.

Portail de la chimie

This article is issued from Wikipédia - version of the Sunday, June 07, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.