
Limite de Roche
Contexte des ??coles Wikip??dia
SOS Enfants a essay?? de rendre le contenu plus accessible Wikipedia par cette s??lection des ??coles. M??res SOS chaque regard apr??s une une famille d'enfants parrain??s .





La limite de Roche ( / ʁoʃ /), parfois d??sign?? sous le rayon Roche, est la distance ?? l'int??rieur duquel un corps c??leste, maintenus ensemble uniquement par sa propre gravit?? , se d??sint??grer en raison de son un deuxi??me corps c??leste les forces de mar??e gravitationnelle d??passant auto-activit?? de la premi??re instance. L'int??rieur de la limite de Roche, mat??riau orbite aura tendance ?? se disperser et de la forme des anneaux, tandis qu'?? l'ext??rieur de la limite, le mat??riel aura tendance ?? fusionner. Le terme est nomm?? d'apr??s ??douard Roche, le Fran??ais astronome qui le premier a calcul?? cette limite th??orique en 1848.
Explication
Typiquement, la limite de Roche se applique ?? un d??sint??gration par satellite en raison de la force des mar??es induites par son primaire, le corps autour duquel il orbites. Pi??ces du satellite qui sont plus pr??s de la primaire sont attir??s par gravit?? plus forte de la primaire, alors que les parties plus loin sont repouss??s par plus fort la force centrifuge de l'orbite du satellite incurv??e. Certains satellites r??els, ?? la fois naturel et artificielle, peut en orbite dans leurs limites Roche parce qu'ils sont maintenus ensemble par des forces autres que la gravitation. Jupiter moon s ' M??tis et Saturne lune de Pan sont des exemples de ces satellites, qui d??tiennent ensemble en raison de leur r??sistance ?? la traction (ce qui signifie qu'ils sont solides et pas facilement tir?? ?? part). Dans les cas extr??mes, des objets reposant sur la surface d'un tel satellite pourrait effectivement ??tre lev??es loin par les forces de mar??e. Un satellite plus faible, comme une com??te , pourrait ??tre bris?? lors de son passage ?? l'int??rieur de sa limite de Roche.
Depuis que les forces de mar??e submerger la gravit?? qui pourrait tenir le satellite ensemble dans la limite de Roche, aucun grand satellite peut fusionner gravitationnellement sur les petites particules ?? l'int??rieur de cette limite. En effet, presque tous connus anneaux plan??taires sont situ??s au sein de leur limite de Roche, Saturne E-Ring et Phoebe anneau ??tant des exceptions notables. Ils pourraient ??tre soit des restes de la plan??te de la proto-plan??taire disque d'accr??tion qui a ??chou?? ?? se fondre en lunes, ou inversement ont form?? quand une lune passait ?? sa limite Roche et se est disloqu??.
Il est ??galement int??ressant de consid??rer que la limite de Roche ne est pas le seul facteur qui provoque com??tes se brisent. Fractionnement par le stress thermique, interne la pression du gaz et le fractionnement de rotation des moyens plus probables pour une com??te pour diviser en situation de stress.
D??termination de la limite de Roche
La distance limite ?? laquelle un satellite peut approcher sans rupture d??pend de la rigidit?? du satellite. ?? un extr??me, un satellite sera compl??tement rigide maintenir sa forme jusqu'?? ce que les forces de mar??e le briser. ?? l'autre extr??me, un satellite tr??s fluide d??forme progressivement conduisant ?? une augmentation des forces de mar??e, provoquant le satellite se allonger, ce qui aggrave encore les forces de mar??e et la casser part plus facilement. La plupart des satellites r??elles se situeraient quelque part entre ces deux extr??mes, avec r??sistance ?? la traction rendant le satellite ni parfaitement rigide ni parfaitement fluide. La limite de Roche est aussi g??n??ralement calcul?? pour le cas d'une orbite circulaire, mais il est facile de modifier le calcul de se appliquer ?? l'affaire (par exemple) d'un corps passant primaire sur une trajectoire parabolique ou hyperbolique.
Calcul rigide par satellite
La limite de Roche corps rigide est un calcul simplifi?? pour un satellite sph??rique, o?? la d??formation du corps par l'effet des mar??es est n??glig??e. Le corps est suppos?? maintenir son sph??rique forme tout en ??tant maintenus ensemble uniquement par sa propre auto-gravit??. D'autres effets sont ??galement n??glig??es, telles que la d??formation de mar??e de la primaire, la rotation et de l'orbite du satellite, et sa forme irr??guli??re. Ces hypoth??ses, bien que r??aliste, simplifient grandement le calcul Roche-limite.
La limite de Roche pour un satellite sph??rique rigide hors effets orbitales, est la distance,  , Du primaire ?? laquelle la force gravitationnelle sur une masse de test sur la surface de l'objet est exactement ??gale ?? la force de mar??e tirant l'objet loin de l'objet:
, Du primaire ?? laquelle la force gravitationnelle sur une masse de test sur la surface de l'objet est exactement ??gale ?? la force de mar??e tirant l'objet loin de l'objet:
o??  est le rayon du primaire,
est le rayon du primaire, 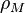 est la densit?? du primaire, et
est la densit?? du primaire, et 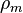 est la densit?? du satellite. Ceci peut se ??crire sous la forme ??quivalente
est la densit?? du satellite. Ceci peut se ??crire sous la forme ??quivalente
o??  est le rayon du secondaire,
est le rayon du secondaire, 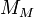 est la masse du primaire, et
est la masse du primaire, et 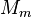 est la masse du secondaire.
est la masse du secondaire.
Notez que cela ne d??pend pas de la taille de l'objet en orbite est, mais seulement sur le rapport des densit??s. Ce est la distance orbitale ?? l'int??rieur duquel mat??riau en vrac (par exemple, regolith ou roches d??tach??es) sur la surface du satellite le plus proche du primaire ne se arracher, et de m??me mat??riau sur le c??t?? oppos?? au primaire sera ??galement tir?? loin de, plut??t que vers le satellite.
Si le satellite est plus de deux fois plus dense que le primaire, comme on peut facilement ??tre le cas pour une lune rocheuse orbitant autour d'une g??ante gazeuse, la limite de Roche sera dans le primaire et donc pas pertinent.
D??rivation de la formule

Afin de d??terminer la limite de Roche, nous consid??rons une petite masse 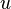 sur la surface du satellite le plus proche du primaire. Il ya deux forces sur cette masse
sur la surface du satellite le plus proche du primaire. Il ya deux forces sur cette masse 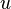 : La force d'attraction vers le satellite et la force d'attraction vers le primaire. Si l'on suppose que le satellite se trouve dans chute libre autour de la primaire et que la force de mar??e est la seule dur??e pertinente de l'attraction gravitationnelle de la primaire. Cette hypoth??se est une simplification que la chute libre se applique uniquement vraiment le centre plan??taire, mais suffira pour cette d??rivation.
: La force d'attraction vers le satellite et la force d'attraction vers le primaire. Si l'on suppose que le satellite se trouve dans chute libre autour de la primaire et que la force de mar??e est la seule dur??e pertinente de l'attraction gravitationnelle de la primaire. Cette hypoth??se est une simplification que la chute libre se applique uniquement vraiment le centre plan??taire, mais suffira pour cette d??rivation.
L'attraction gravitationnelle  sur la masse
sur la masse 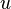 vers le satellite avec la masse
vers le satellite avec la masse 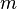 et le rayon
et le rayon  peut ??tre exprim??e en fonction de La loi de la gravitation de Newton.
peut ??tre exprim??e en fonction de La loi de la gravitation de Newton.
la force de mar??e  sur la masse
sur la masse 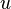 vers le primaire de rayon
vers le primaire de rayon 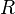 et la masse
et la masse  , ?? une distance
, ?? une distance  entre les centres des deux organes, peut ??tre exprim??e approximativement comme
entre les centres des deux organes, peut ??tre exprim??e approximativement comme
 .
.
Pour obtenir cette approximation, pour la diff??rence de l'attraction gravitationnelle du primaire sur le centre du satellite et sur le bord du satellite le plus proche du primaire:
Dans l'approximation o?? r <  dans le num??rateur et chaque terme avec
dans le num??rateur et chaque terme avec  dans le d??nominateur tend vers z??ro, ce qui nous donne:
dans le d??nominateur tend vers z??ro, ce qui nous donne:
La limite de Roche est atteint lorsque la force gravitationnelle et la force de mar??e se ??quilibrent.
ou
 ,
,
qui donne la limite de Roche,  , Comme
, Comme
 .
.
Cependant, nous ne voulons pas vraiment le rayon du satellite appara??t dans l'expression de la limite, de sorte que nous r??-??crire ce en termes de densit??.
Pour une sph??re la masse  peut se ??crire
peut se ??crire
 o??
o?? 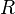 est le rayon du primaire.
est le rayon du primaire.
Et de m??me
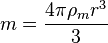 o??
o??  est le rayon du satellite.
est le rayon du satellite.
En rempla??ant les masses dans l'??quation de la limite de Roche, et annulant  donne
donne
 ,
,
qui peut ??tre simplifi?? ?? la limite de Roche:
 .
.
Satellites fluides
Une approche plus pr??cise pour le calcul de la limite de Roche prend la d??formation du satellite en compte. Un exemple extr??me serait une verrouillage gravitationnel satellite en orbite une plan??te liquide, o?? toute force agissant sur le satellite serait d??former dans une prolate sph??ro??de.
Le calcul est complexe et son r??sultat ne peut pas ??tre repr??sent?? dans une formule alg??brique exacte. Roche se est d??riv??e la solution approximative suivante pour la limite de Roche:
Cependant, une meilleure approximation qui prend en compte l'aplatissement de la primaire et la masse du satellite est:
o?? 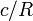 est le aplatissement de la primaire. Le facteur num??rique est calcul??e ?? l'aide d'un ordinateur.
est le aplatissement de la primaire. Le facteur num??rique est calcul??e ?? l'aide d'un ordinateur.
La solution liquide est appropri??e pour des corps qui ne sont que l??g??rement fix??es, comme une com??te. Par exemple, la com??te D??composition de l'orbite de Shoemaker-Levy 9 autour de Jupiter a adopt?? dans son limite de Roche en Juillet 1992, l'amenant ?? se fragmenter en plusieurs petits morceaux. Sur sa prochaine d??marche en 1994, les fragments se sont ??cras??s sur la plan??te. Shoemaker-Levy 9 a ??t?? observ?? pour la premi??re en 1993, mais son orbite a indiqu?? qu'il avait ??t?? captur?? par Jupiter quelques d??cennies avant.
D??rivation de la formule
Comme le cas par satellite fluide est plus d??licate que celle rigide, le satellite est d??crite avec quelques hypoth??ses simplificatrices. Tout d'abord, assumer l'objet se compose de fluide incompressible qui a densit?? constante 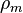 et le volume
et le volume  qui ne d??pendent pas de forces externes ou internes.
qui ne d??pendent pas de forces externes ou internes.
Deuxi??mement, assumer le satellite se d??place sur une orbite circulaire et il reste en rotation synchrone. Cela signifie que la vitesse angulaire 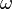 au cours de laquelle il tourne autour de son centre de masse est la m??me que la vitesse angulaire ?? laquelle il se d??place autour de l'ensemble du syst??me barycentre.
au cours de laquelle il tourne autour de son centre de masse est la m??me que la vitesse angulaire ?? laquelle il se d??place autour de l'ensemble du syst??me barycentre.
La vitesse angulaire 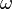 est donn??e par la troisi??me loi de Kepler :
est donn??e par la troisi??me loi de Kepler :
Lorsque M est beaucoup plus grand que m, ce sera pr??s de
La rotation synchrone signifie que le liquide ne se d??place pas et que le probl??me peut ??tre consid??r??e comme statique. Par cons??quent, la viscosit?? et frottement du liquide dans ce mod??le ne joue pas un r??le, puisque ces quantit??s joueraient un r??le que pour un fluide en mouvement.
Compte tenu de ces hypoth??ses, les forces suivantes doivent ??tre prises en compte:
- La force de gravitation due au corps principal;
- la la force centrifuge dans le syst??me de r??f??rence en rotation; et
- le champ auto-gravitation du satellite.
Comme toutes ces forces sont conservateurs, ils peuvent ??tre exprim??s ?? l'aide d'un potentiel. En outre, la surface du satellite est une une ??quipotentielle. Sinon, les diff??rences de potentiel donneraient lieu ?? des forces et le mouvement de certaines parties du liquide ?? la surface, ce qui contredit l'hypoth??se de mod??le statique. Compte tenu de la distance entre le corps principal, notre probl??me est de d??terminer la forme de la surface qui satisfait ?? la condition de potentiel.
Comme l'a suppos?? orbite circulaire, la force de gravitation totale et de la force centrifuge agissant sur le corps principal annuler. Par cons??quent, la force qui affecte les particules du liquide est la force de mar??e, qui d??pend de la position par rapport au centre de masse, d??j?? pris en compte dans le mod??le rigide. Pour les petits corps, la distance entre les particules liquides du centre du corps est faible par rapport ?? la distance d au corps principal. Ainsi, la force de mar??e peut ??tre lin??aris??, ce qui entra??ne dans la m??me formule pour F T comme indiqu?? ci-dessus. Bien que cette force dans le mod??le rigide ne d??pend que du rayon r du satellite, dans le cas de fluide, nous devons tenir compte de tous les points de la surface et de la force des mar??es d??pend de la distance Dd du centre de masse ?? une particule donn??e projet??e sur la ligne joignant le satellite et le corps principal. Nous appelons Dd la distance radiale. ??tant donn?? que la force de mar??e est lin??aire dans Dd, le potentiel li?? est proportionnelle au carr?? de la variable et pour 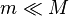 nous avons
nous avons
On veut d??terminer la forme du satellite pour lequel la somme du potentiel d'auto-gravitation et 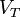 est constante sur la surface du corps. En g??n??ral, un tel probl??me est tr??s difficile ?? r??soudre, mais dans ce cas particulier, il peut ??tre r??solu par une conjecture habile en raison de la d??pendance carr?? du potentiel de mar??e sur la distance radiale Dd
est constante sur la surface du corps. En g??n??ral, un tel probl??me est tr??s difficile ?? r??soudre, mais dans ce cas particulier, il peut ??tre r??solu par une conjecture habile en raison de la d??pendance carr?? du potentiel de mar??e sur la distance radiale Dd
??tant donn?? que le potentiel V T change dans une seule direction, ce est ?? dire la direction vers le corps principal, le satellite peut se attendre ?? prendre une forme ?? sym??trie axiale. Plus pr??cis??ment, nous pouvons supposer que cela prend la forme d'un solide de r??volution. L'auto-potentiel sur la surface d'un tel solide de r??volution ne peut d??pendre de la distance radiale au centre de masse. En effet, l'intersection du satellite et d'un plan perpendiculaire ?? la ligne joignant les corps est un disque dont le bord de nos hypoth??ses est un cercle de potentiel constant. Si la diff??rence entre l'auto-gravitation potentiel et V T ??tre constante, les deux potentiels doivent d??pendent de la m??me mani??re sur Dd. En d'autres termes, l'auto-potentiel doit ??tre proportionnelle au carr?? de Dd. Ensuite, il peut ??tre d??montr?? que la solution ??quipotentielle est un ellipso??de de r??volution. Compte tenu de la densit?? et un volume constant d'auto-potentiel d'un tel corps ne d??pend que de la excentricit?? ε de l'ellipso??de:
o?? 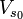 est l'auto-potentiel constant sur l'intersection du bord circulaire du corps et le plan m??dian de sym??trie ??tant donn?? par l'??quation Dd = 0.
est l'auto-potentiel constant sur l'intersection du bord circulaire du corps et le plan m??dian de sym??trie ??tant donn?? par l'??quation Dd = 0.
La fonction f dimension est d??termin??e ?? partir de la solution exacte pour le potentiel de l'ellipso??de
et, de fa??on assez surprenante, ne d??pend pas sur le volume du satellite.
Bien que la forme explicite de la fonction f semble compliqu??, il est clair que nous pouvons et ne choisissons la valeur de ε de sorte que le potentiel V T est ??gale ?? V S plus une constante ind??pendante de la variable Dd. Par inspection, cela se produit lorsque
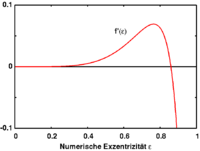
Cette ??quation peut ??tre r??solue num??riquement. Le graphique indique qu'il existe deux solutions et donc la plus petite repr??sente une forme d'??quilibre stable (l'ellipso??de avec la plus petite excentricit??). Cette solution d??termine l'excentricit?? de l'ellipso??de des mar??es en fonction de la distance par rapport au corps principal. La d??riv??e de la fonction f a une excentricit?? z??ro lorsque le maximum est atteint. Cela correspond ?? la limite de Roche.
Plus pr??cis??ment, la limite de Roche est d??termin??e par le fait que la fonction f, qui peut ??tre consid??r??e comme une mesure non lin??aire de la force de serrage de l'ellipso??de vers une forme sph??rique, est limit??e de sorte qu'il existe une excentricit?? ?? laquelle cette force de contraction devient maximale . Depuis les mar??es force augmente lorsque le satellite se approche le corps principal, il est clair qu'il ya une distance critique ?? laquelle l'ellipso??de est d??chir??.
L'excentricit?? maximale peut ??tre calcul??e num??riquement en tant que z??ro de la d??riv??e de f '. On obtient
qui correspond au rapport des axes de l'ellipso??de 1: 1,95. Insertion ce dans la formule de la fonction f peut d??terminer la distance minimale ?? laquelle l'ellipso??de existe. Ce est la limite de Roche,
Roche limites pour exemples choisis
Le tableau ci-dessous montre la densit?? moyenne et le rayon ??quatorial pour les objets s??lectionn??s dans le syst??me solaire .
| Primaire | Densit?? (kg / m??) | Rayon (m) |
|---|---|---|
| Soleil | 1408 | 696000000 |
| Jupiter | 1326 | 71492000 |
| Terre | 5513 | 6378137 |
| Lune | 3346 | 1738100 |
| Saturne | 687 | 60268000 |
| Uranus | 1318 | 25559000 |
| Neptune | 1638 | 24764000 |
Gr??ce ?? ces donn??es, les limites Roche pour corps rigides et fluides peuvent ??tre facilement calcul??s. La densit?? moyenne des com??tes est prise ??gale ?? environ 500 kg / m??.
Le tableau ci-dessous donne les limites Roche exprim??es en m??tres et en rayons primaire. La vraie limite de Roche pour un satellite d??pend de sa densit?? et la rigidit??.
| Corps | Satellite | Limite de Roche (rigide) | Limite de Roche (fluide) | ||
|---|---|---|---|---|---|
| Distance (km) | R | Distance (km) | R | ||
| Terre | Lune | 9496 | 1,49 | 18261 | 2,86 |
| Terre | com??te moyenne | 17880 | 2,80 | 34390 | 5,39 |
| Soleil | Terre | 554400 | 0,80 | 1066300 | 1,53 |
| Soleil | Jupiter | 890700 | 1,28 | 1713000 | 2,46 |
| Soleil | Lune | 655300 | 0,94 | 1260300 | 1,81 |
| Soleil | com??te moyenne | 1234000 | 1,78 | 2374000 | 3,42 |
Si le primaire est inf??rieure ?? la moiti?? aussi dense que le satellite, la limite de Roche de corps rigide est inf??rieure ?? rayon de la primaire, et les deux corps peut entrer en collision avant la limite de Roche est atteint.
?? quelle distance des lunes du syst??me solaire ?? leurs limites Roche? Le tableau ci-dessous donne le rayon orbital de chaque satellite int??rieure divis??e par son propre rayon de Roche. Les deux calculs de corps rigide et fluidis?? sont donn??s. Note Pan, M??tis et Na??ade en particulier, qui peut ??tre assez proche de leurs points morts-up r??els.
Dans la pratique, les densit??s de la plupart des satellites des plan??tes g??antes int??rieures ne sont pas connus. Dans ces cas, en italique, les valeurs probables ont ??t?? pris, mais leur limite r??elle Roche peuvent varier de la valeur indiqu??e.
| Primaire | Satellite | Orbital limite Radius / Roche | |
|---|---|---|---|
| (Rigide) | (Fluide) | ||
| Soleil | Mercure | 104: 1 | 54: 1 |
| Terre | Lune | 41: 1 | 21: 1 |
| Mars | Phobos | 172% | 89% |
| Deimos | 451% | 234% | |
| Jupiter | M??tis | ~ 186% | ~ 94% |
| Adrastea | ~ 188% | ~ 95% | |
| Amalthea | 175% | 88% | |
| L'??tre | 254% | 128% | |
| Saturne | Casserole | 142% | 70% |
| Atlas | 156% | 78% | |
| Prom??th??e | 162% | 80% | |
| Pandora | 167% | 83% | |
| Epim??th??e | 200% | 99% | |
| Janus | 195% | 97% | |
| Uranus | Cordelia | ~ 154% | ~ 79% |
| Ophelia | ~ 166% | ~ 86% | |
| Bianca | ~ 183% | ~ 94% | |
| Cressida | ~ 191% | ~ 98% | |
| Desdemona | ~ 194% | ~ 100% | |
| Juliet | ~ 199% | ~ 102% | |
| Neptune | Na??ade | ~ 139% | ~ 72% |
| Thalassa | ~ 145% | ~ 75% | |
| Despina | ~ 152% | ~ 78% | |
| Galatea | 153% | 79% | |
| Larissa | ~ 218% | ~ 113% | |
| Pluton | Charon | 12,5: 1 | 6,5: 1 |


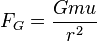
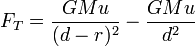

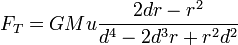

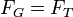
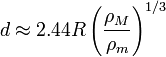
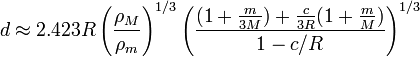



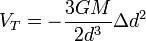

![f (\ epsilon) = \ frac {1 - \ epsilon ^ 2} {\ epsilon ^ 3} \ cdot \ left [\ left (3- \ epsilon ^ 2 \ right) \ cdot \ mathrm {arcsinh} \ left (\ frac {\ epsilon} {\ sqrt {1- \ epsilon ^ 2}} \ right) -3 \ epsilon \ right]](../../images/1502/150266.png)


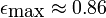
![d \ environ 2 {.} 423 \ cdot R \ cdot \ sqrt [3] {\ frac {\ rho_M} {\ rho_m}} \ ,.](../../images/1502/150277.png)
