Histogramme

Saviez-vous ...

SOS Enfants, qui se d??roule pr??s de 200 sos ??coles dans le monde en d??veloppement, a organis?? cette s??lection. Pour comparer les organismes de bienfaisance de parrainage ce est le meilleur lien de parrainage .

Un exemple histogramme des hauteurs de 31 Arbres Black Cherry.

Dans les statistiques , un histogramme est un affichage graphique des tableaux fr??quences. Un histogramme est la version graphique d'un tableau qui montre quelle proportion des cas entrant dans chacune de plusieurs ou beaucoup ont sp??cifi?? cat??gories. L'histogramme est diff??rent d'un histogramme en ce qu'elle est la zone de la barre qui indique la valeur, pas la hauteur, une distinction cruciale lorsque les cat??gories ne sont pas de largeur uniforme (Lancaster, 1974). Les cat??gories sont g??n??ralement sp??cifi??es comme non-chevauchement intervalles de certaines variables. Les cat??gories (bars) doivent ??tre adjacentes.

Le mot histogramme est d??riv?? de grec : histos de la chose mis debout ??(comme les m??ts d'un navire, la barre d'un m??tier, ou les barres verticales d'un histogramme); 'dessin, dossier, ??crit Gramma. L'histogramme est l'un des sept outils de base de contr??le de la qualit??, qui comprennent aussi le Diagramme de Pareto, v??rifier avec la feuille, carte de contr??le, diagramme et de cause ?? effet, organigramme, et diagramme de dispersion. Une g??n??ralisation de l'histogramme est noyau techniques de lissage. Ce sera la construction d'un tr??s lisse fonction de densit?? de probabilit?? ?? partir des donn??es fournies.

Exemples

Comme exemple, nous consid??rons les donn??es recueillies par le Bureau du recensement des ??tats-Unis ?? temps pour se rendre au travail (recensement de 2000, , Tableau 5). Le recensement a r??v??l?? que il y avait 124 millions de personnes qui travaillent ?? l'ext??rieur de leurs maisons. Les gens ont ??t?? demand?? combien de temps il leur faut pour se rendre au travail, et leurs r??ponses ont ??t?? divis??s en cat??gories: moins de 5 minutes, plus de 5 minutes et moins de 10, plus de 10 minutes et moins de 15, et ainsi de suite. Les tableaux montrent le nombre de personnes par cat??gorie en milliers, de sorte que 4180 signifie 4180000.

Les donn??es dans les tableaux suivants sont affich??s graphiquement par histogrammes. Une caract??ristique int??ressante de deux diagrammes est la pointe dans la cat??gorie 30 minutes. Il semble probable que ce est un artefact: une demi-heure est une unit?? de mesure commune de temps informelle, afin que les gens dont les temps de Voyage ??taient peut-??tre un peu moins ou un peu plus que 30 minutes pourraient ??tre enclins ?? r??pondre ?? "30 minutes". Cet arrondi est un ph??nom??ne commun lors de la collecte des donn??es de personnes.

Histogramme de temps de Voyage, recensement am??ricain 2000. L'aire sous la courbe est ??gal au nombre total de cas. Ce sch??ma utilise Q / largeur de la table.

Donn??es en chiffres absolus
Intervalle	Largeur	Quantit??	Quantit?? / largeur
0	5	4180	836
5	5	13687	2737
10	5	18618	3723
15	5	19634	3926
20	5	17981	3596
25	5	7190	1438
30	5	16369	3273
35	5	3212	642
40	5	4122	824
45	15	9200	613
60	30	6461	215
90	60	3435	57

Cet histogramme montre le nombre de cas par intervalle unit?? afin que la hauteur de chaque barre est ??gale ?? la proportion de personnes au total dans l'enqu??te qui tombent dans cette cat??gorie. L'aire sous la courbe repr??sente le nombre total de cas (124 000 000). Ce type d'histogramme montre nombres absolus.

Histogramme de temps de Voyage, recensement am??ricain 2000. Aire sous la courbe est ??gal ?? 1. Ce sch??ma utilise Q / totale / largeur de la table.

Donn??es par part
Intervalle	Largeur	Quantit?? (Q)	Q / totale / largeur
0	5	4180	0,0067
5	5	13687	0,0220
10	5	18618	0,0300
15	5	19634	0,0316
20	5	17981	0,0289
25	5	7190	0,0115
30	5	16369	0,0263
35	5	3212	0,0051
40	5	4122	0,0066
45	15	9200	0,0049
60	30	6461	0,0017
90	60	3435	0,0004

Cet histogramme diff??re de la premi??re que dans la ??chelle verticale. La hauteur de chaque barre est le pourcentage du total d??cimal qui repr??sente chaque cat??gorie, et la surface totale de toutes les barres est ??gale ?? 1, l'??quivalent d??cimal de 100%. La courbe affich??e est simple estimation de la densit??. Cette version montre proportions, et est ??galement connu comme un histogramme de surface unitaire.

En d'autres termes un histogramme repr??sentant une distribution de fr??quence au moyen de rectangles dont les largeurs repr??sentent des intervalles de classe et dont les zones sont proportionnelles aux fr??quences correspondantes. Ils ne placent les barres ensemble pour rendre plus facile de comparer les donn??es.

Activit??s et manifestations

Le Pages de ressources Socr contiennent un certain nombre de mains sur les activit??s interactives d??montrant le concept d'un histogramme, histogramme construction et manipulation aide d'applets Java et charts.

D??finition math??matique

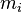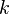Dans un sens plus g??n??ral math??matique, un histogramme est un mappage $m_i$ qui compte le nombre d'observations qui tombent dans plusieurs cat??gories disjointes (appel??s bacs), tandis que la courbe d'histogramme est simplement une mani??re de repr??senter un histogramme. Ainsi, si nous laissons $n$ le nombre total d'observations et $k$ le nombre total d'intervalles, l'histogramme 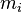$m_i$ remplit les conditions suivantes:

$n = \ sum_ {i = 1} ^ k {} m_i.$

Histogramme cumulatif

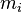Un histogramme cumulatif est une application qui compte le nombre cumul?? de l'ensemble des observations dans les bacs jusqu'au r??ceptacle sp??cifi??. Autrement dit, l'histogramme cumul?? $M_i$ d'un histogramme $m_i$ est d??fini comme:

$M_i = \ sum_ {j = 1} ^ i {} m_j$

Nombre de bacs et la largeur

Il n'y a pas ??meilleur?? nombre de bacs, et diff??rentes tailles de poubelles peut r??v??ler des caract??ristiques diff??rentes des donn??es. Certains th??oriciens ont tent?? de d??terminer un nombre optimal de classes, mais ces m??thodes g??n??ralement faire des hypoth??ses fortes sur la forme de la distribution. Vous devriez toujours exp??rimenter avec des largeurs de casier avant de choisir un (ou plusieurs) qui illustrent les principales caract??ristiques de vos donn??es.

Le nombre de bacs 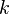$k$ peut ??tre calcul??e directement, ou ?? partir d'une largeur de casier sugg??r?? $h$ :

$k = \ left \ lceil \ frac {\ max x - \ min x} {h} \ right \ rceil$

Les accolades indiquent la fonction de plafond.

La formule de Sturges: $k = \ lceil \ log_2 n + 1 \ rceil$

qui fonde implicitement les tailles bin sur la gamme des donn??es, et peut effectuer mal si 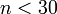$n <30$ .

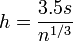
Le choix de Scott: $h = \ frac {3,5} s {n ^ {1/3}}$

o?? $h$ est la largeur commune bin, et $s$ l'??chantillon est l'??cart type .

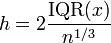
Le choix de Freedman-Diaconis: $h = 2 \ frac {\ operatorname {IQR} (x)} {n ^ {1/3}}$

qui est bas?? sur la gamme interquartile

Continue des donn??es

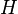L'id??e d'un histogramme peut ??tre g??n??ralis??e ?? des donn??es continues. Laisser $f \ in L ^ 1 (R)$ (Voir Lebesgue espace), l'op??rateur de l'histogramme cumulatif $H$ peut ??tre d??fini par:

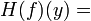$H (f) (y) =$ avec seulement un nombre fini des intervalles de monotonie cela peut ??tre r????crite comme

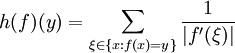$h (f) (y) = \ sum _ {\ xi \ in \ {x: f (x) = y \}} \ frac {1} {| f '(\ xi) |}$ .

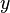$H (f) (y)$ est ind??fini si $y$ est la valeur d'un point fixe.

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Histogram&oldid=203161357 "