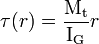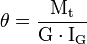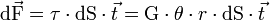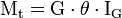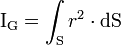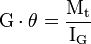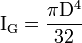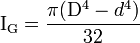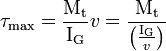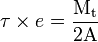Torsion

Cet article est une ébauche concernant la mécanique.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

Pour les articles homonymes, voir Torsion (homonymie).

Sapin tordu et couché par la bise

La torsion est le fait de vriller une pièce, comme lorsque l'on essore une serpillière — notons que dans le langage courant, « tordre » désigne plutôt ce que l'on appelle la flexion en mécanique.

Pour être plus précis, la torsion est la sollicitation subie par un corps soumis à l'action d'un couple de forces opposées agissant dans des plans parallèles et dont l'élément de réduction est un moment de force agissant dans l'axe de la poutre.

Applications

Arbres de transmission

Pétrin mécanisé (XIX^e siècle) : l'arbre, suspendu au plafond, transmet l'effort entre le moteur (sous le plan de travail à gauche) et le pétrin à droite (transmisison par poulies-courroies)

Modèle mécanique de l'arbre et diagramme du moment de torsion M_t : idéal (sans frottement) en noir, réel en bleu.

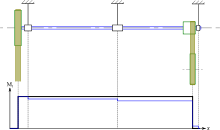
Les arbres de transmission mécanique sont un exemple typique de torsion. En régime permanent (hors démarrage, arrêt de la machine et changement de régime), l'arbre est animé d'un mouvement de rotation uniforme. Le couple moteur s'équilibre avec le couple résistant (frottements des paliers) et la charge (effort fourni par la machine). Ainsi, bien que le système soit en mouvement, on peut l'étudier par la statique.

Si l'on néglige les frottements, alors le couple charge C_c est égal en intensité au couple moteur C_m. L'arbre est à l'équilibre sous l'effet de ces deux couples opposés, le moment de torsion M_t est uniforme (M_t = C_c = C_m en valeur absolue). Si l'on prend en compte les frottements dans les paliers, alors le C_c < C_m, et M_t est uniforme par parties.

Notons que les courroies exercent une force vers le bas (une tension de courroie est nécessaire à la transmission par adhérence), l'arbre est donc également soumis à de la flexion.

Ressorts et assimilés

Ressort hélicoïdal de torsion

Un ressort est une pièce destinée à opposer un effort en se déformant. Lorsque l'on parle de torsion, il faut distinguer trois cas :

les ressorts de torsion : leur rôle est d'opposer un couple, un « effort tournant », c'est le cas par exemple du ressort de la pince à linge ; du point de vue de la matière, le fil de ce ressort se déforme en flexion ;
les ressorts dont la matière est soumise à de la torsion : c'est le cas des ressorts de traction et des ressorts de compression (resorts hélicoïdaux).
les barres et fils de torsion : ce sont des ressorts de torsion dont la matière se déforme en torsion :
- les barres de torsion sont des barres métalliques peu déformables (rigide) ; elles sont notamment utilisées pour la suspension de véhicules automobiles,
- La balance de torsion est un appareil servant à mesurer l'intensité de petites forces au moyen du couple de torsion d'un fil métallique.

Torsion en théorie des poutres

Moments de force résultant de l'action d'un couple de forces dans deux plans parallèles

Torsion uniforme et non uniforme

La torsion s'exprime sous la forme d'un moment de torsion M_t agissant dans l'axe x de la poutre. Sous l'effet de la torsion, les sections transversales de la poutre ne restent généralement pas planes, on doit abandonner l'hypothèse de Bernoulli ; on dit qu'elles « gauchissent ». Lorsque leur gauchissement est libre, seules des contraintes tangentielles τ apparaissent et la poutre n'est soumise qu'à de la torsion dite « uniforme » (ou « torsion de Saint-Venant »).

Lorsque leur gauchissement est empêché, par exemple par un encastrement en rotation, ou que le moment de torsion n'est pas constant, provoquant un gauchissement variable d'une section transversale à l'autre, des contraintes normales σ apparaissent en plus des contraintes de cisaillement et la barre est soumise à de la torsion « non uniforme ».

La torsion non uniforme est toujours accompagnée de la torsion uniforme. Le moment de torsion M_t peut donc se décomposer en la somme

d'une part uniforme M_v (générant de la contrainte tangentielle τ) et
d'une part non uniforme M_w (générant de la contrainte normale σ).

Une section fermée ou trapue (compacte) travaille principalement en torsion uniforme ; dans le cas d'une poutre dont la section présente une symétrie de révolution (section circulaire ou annulaire par exemple), les contraintes de cisaillement varient de manière linéaire lorsque l'on s'éloigne de la fibre neutre.

Les sections ouvertes ou sans symétrie de révolution travaillent principalement en torsion non uniforme et le problème est plus complexe. En particulier, la contrainte à une surface libre (qui n'est pas en contact avec une autre pièce) est nécessairement dans le plan tangent à cette surface, et notamment la contrainte à un angle libre est nécessairement nulle.

Lorsqu'aucune part de torsion n'est prédominante, on parle de « torsion mixte » ; c'est le cas notamment des profilés laminés.

Torsion uniforme d'un arbre circulaire

Déformation

Déformation d'une génératrice et angle de torsion

Considérons une poutre de longueur L, encastrée à une extrémité, l'autre extrémité étant libre. Traçons un rayon sur la section droite de l'extrémité libre ; en petites déformations, on suppose que ce rayon reste rectiligne, il tourne d'un angle α. On suppose que la déformation est homogène, l'angle duquel tourne une section droite quelconque dépend de manière linéaire de la distance à l'encastrement. On définit le taux de rotation, ou angle unitaire de torsion θ par :

θ = α/L ;

θ s'exprime en radian par mètre (rad/m).

Si l'on trace une génératrice, celle-ci prend la forme d'une hélice.

Contraintes

Répartition des contraintes sur l'axe vertical dans le cas d'un arbre plein (gauche) et d'un tube (droite).

Selon la théorie d'Euler-Bernoulli, si l'on reste en petites déformations, le moment de torsion M_t crée des cissions (contraintes de cisaillement) τ qui sont proportionnelles à la distance r par rapport à l'axe de torsion :

\tau(r) = \frac{\mathrm{M_t}}{\mathrm{I_G}} r

où

M_t est le moment de torsion ;
I_G est le moment quadratique de torsion, dépendant de la forme de la section (diamètre extérieur, et diamètre intérieur dans le cas d'un tube).

L'angle unitaire de torsion est donné par

\theta = \frac{\mathrm{M_t}}{\mathrm{G} \cdot \mathrm{I_G}}

Démonstration

Déformation en cisaillement.

Considérons deux points d'une génératrice du cylindre, A et B, situés à une distance respective x et x + dx de la partie encastrée, et à une même distance r de la fibre neutre (axe du cylindre). Avec la torsion, ils restent sur leur section droite respective (torsion uniforme) et se déplacent sur un cercle de centre G et de rayon r ; ils deviennent respectivement A' et B'.

Le point A tourne d'un angle θ×x, donc se déplace sur un arc de longueur u_A = θ×x×r. De même, le point B se déplace d'une quantité u_B = θ×(x + dx)×r. La déformation vaut donc

γ = du/dx = (u_B - u_A)/dx = θ×r.

On en déduit que

la déformation γ varie linéairement avec r.

Donc, d'après la loi de Hooke en cisaillement, la contrainte varie également de manière linéaire :

τ(r ) = G×γ(r ) = G×θ×r,

la quantité G×θ étant à déterminer. Un petit élément de surface dS autour de A reçoit une force dF valant

\mathrm{d}\vec{\mathrm{F}} = \tau \cdot \mathrm{dS} \cdot \vec{t} = \mathrm{G} \cdot \theta \cdot r \cdot \mathrm{dS}\cdot \vec{t}

où $\vec(t)$ est le vecteur tangent au cercle de déplacement.

Le moment dM de cette force par rapport au point G (0,0,0) appartenant donc à la ligne moyenne vaut :

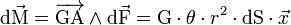\mathrm{d}\vec{\mathrm{M}} = \overrightarrow{\mathrm{GA}} \wedge \mathrm{d}\vec{\mathrm{F}} = \mathrm{G} \cdot \theta \cdot r^2 \cdot \mathrm{dS} \cdot \vec{x}

Le moment de torsion résulte de l'ensemble de ces moments, et en intégrant sur la section droite, on trouve :

\mathrm{M_t} = \mathrm{G} \cdot \theta \cdot \mathrm{I_G}

avec

\mathrm{I_G} = \int_{\mathrm{S}} r^2 \cdot \mathrm{dS}

On a alors :

\mathrm{G} \cdot \theta = \frac{\mathrm{M_t}}{\mathrm{I_G}}

soit

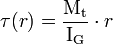\tau(r) = \frac{\mathrm{M_t}}{\mathrm{I_G}} \cdot r

Pour un arbre plein, on a

\mathrm{I_G} = \frac{\pi \mathrm{D}^4}{32}

où D est le diamètre. Pour un tube, on soustrait simplement le moment quadratique de la partie évidée :

\mathrm{I_G} = \frac{\pi ( \mathrm{D}^4 - d^4)}{32}

où D est le diamètre extérieur et d est le diamètre intérieur.

Article détaillé : Moment quadratique.

La cission maximale vaut

\tau_\mathrm{max} = \frac{\mathrm{M_t}}{\mathrm{I_G}} v = \frac{\mathrm{M_t}}{\left ( \frac{\mathrm{I_G}}{v} \right )}

où v est le rayon extérieur de la pièce (D/2). La quantité C = (I_G/v ) est appelée module de torsion.

Unités
Grandeur	Unité internationale	Unité usuelle	Unité pour les calculs
M_t	Nm	Nm	Nmm
I_G	m⁴	cm⁴	mm⁴
v	m	cm	mm
C = (I_G/v )	m³	cm³	mm³
τ	Pa	MPa	MPa

Torsion d'une section prismatique

Torsion d'une barre de section carrée

Le cas des sections non circulaires est plus complexe. En particulier, en un point A donné, le vecteur rayon 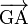$\overrightarrow{\mathrm{GA}}$ n'est pas perpendiculaire au vecteur contrainte en A, ce qui complique le calcul du moment.

Par ailleurs, dans le cas d'une section prismatique, il y a gauchissement de la section (torsion non prismatique).

Les équations de l'élasticité (conditions d'équilibre d'un élément de matière) indiquent qu'à une surface libre, le vecteur contrainte est tangent à la surface ; en particulier, à un angle de la section (c'est-à-dire sur une arête de la poutre), le vecteur contrainte est nul. La contrainte est maximale au milieu des faces libres.

Le tableau suivant donne la composante uniforme de la torsion. La torsion d'un cylindre plein est rappelée à titre de comparaison.

Torsion d'arbres prismatiques
Forme	Contrainte maximale τ_max (MPa)	Angle unitaire de torsion θ (rad/m)
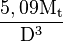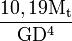Cylindre plein de diamètre D	$\frac{5,09 \mathrm{M_t}}{\mathrm{D}^3}$	$\frac{10,19 \mathrm{M_t}}{\mathrm{G}\mathrm{D}^4}$
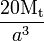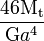Triangle équilatéral de côté a	$\frac{20 \mathrm{M_t}}{a^3}$	$\frac{46 \mathrm{M_t}}{\mathrm{G}a^4}$
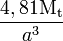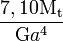Carré de côté a	$\frac{4,81 \mathrm{M_t}}{a^3}$	$\frac{7,10 \mathrm{M_t}}{\mathrm{G}a^4}$
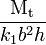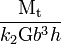Rectangle de côté b×h (h > b)	$\frac{\mathrm{M_t}}{k_1 b^2 h}$	$\frac{\mathrm{M_t}}{k_2 \mathrm{G}b^3 h}$

Contrainte sur les axes y et z

Dans le cas de la section rectangulaire, la contrainte est maximale au milieu de la grande face :

τ_max = τ_z.

La contrainte au milieu de la petite face vaut :

τ_y = η×τ_z = η×τ_max.

Les coefficients k₁, k₂ et η dépendent du rapport h/b et sont donnés dans la table ci-dessous.

Coefficients de la torsion d'une section rectangulaire^[1]^,^[2]
h/b	1	1,2	1,5	1,75	2	2,5	3	4	5	6	8	10	∞
k₁	0,208	0,216	0,231	0,239	0,246	0,258	0,267	0,282	0,291	0,299	0,307	0,313	1/3
k₂	0,140 6	0,166 1	0,195 8	0,214	0,229	0,249	0,263	0,281	0,291	0,299	0,307	0,313	1/3
η	1		0,859	0,820	0,795	0,766	0,753	0,745		0,743		0,742	0,742

Torsion d'une section creuse fermée

Considérons un tube à paroi mince, la forme de la section étant quelconque mais fermée. L'équilibre d'un élément donne tout de suite que le produit de la contrainte moyenne (sur la ligne médiane) par l'épaisseur, $τ\times e$ , est uniforme. On a :

\tau \times e = \frac{\mathrm{M_t}}{2 \mathrm{A}}

où A est l'aire comprise à l'intérieur de la ligne moyenne. Comme la paroi est mince, on peut considérer par approximation que la contrainte maximale est égale à la contrainte moyenne.

Notes et références

↑ Jean-Louis Fanchon, Guide de mécanique, Nathan,‎ 2001 (ISBN 978-2-09-178965-1), p. 315
↑ [(fr) Cours de résistance des matériaux — Torsion (ESTP) (page consultée le 2012-06-19)]

Voir aussi

Liens externes

Éric Davalle, « Torsion uniforme », dans Mécanique des structures I, EPFL (lire en ligne)

Portail des sciences des matériaux

This article is issued from Wikipédia - version of the Saturday, October 24, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.