Théorie néo-classique du producteur
|
|
Cet article est une ébauche concernant l’économie. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
|
La théorie néo-classique du producteur est le pendant de la théorie du consommateur (micro-économie). Il s'agit d'une modélisation économique du comportement d'un agent économique en tant que producteur de biens et de services. L'objectif est de comprendre et d'expliquer le comportement de cet unique producteur en tant qu'agent parfaitement rationnel et parfaitement informé (homo œconomicus). Suivant le cadre néoclassique, on considère comme producteur un agent qui transforme des inputs (appelés plus conventionnellement facteurs de production) en outputs (ou production finale) selon une fonction de production. Cependant, l'analyse du producteur se réalise au sein d'un environnement hypothétique, qui ne reflète en rien la réalité mais qui permet de simplifier grandement l'étude de son comportement. On regroupe habituellement ces hypothèses sous l'appellation : « concurrence pure et parfaite ».
La théorie du producteur, tout comme celle du consommateur, a été développée et soutenue à la fin du XIXe siècle, par deux grands auteurs issus du marginalisme (Léon Walras et Stanley Jevons). Par la suite, elle a été modifiée et complétée par leurs successeurs : A. Marshall, AC. Pigou, V. Pareto, etc.
Programme primal et programme dual
Technologie et ensemble de production
Ensemble de production
Définitions
Le producteur néoclassique est une « boîte noire » : on ne s'intéresse qu'à ce qui entre et à ce qui sort, sans se préoccuper du mode exact de transformation des inputs en outputs. Autrement dit, on ne s'intéresse qu'à la relation quantitative qui existe entre les deux. Les auteurs néo-classiques ont eu l'habitude de recourir, pour exprimer cette relation quantitative, à une expression purement mathématique. Cette relation mathématique entre d'un côté les « facteurs de production » (ce qui sert à produire) et, de l'autre côté, la production finale elle-même, est appelée fonction de production. Elle fournit la quantité maximale que le producteur peut espérer obtenir compte tenu d'une certaine quantité de facteurs de production utilisés.
On peut ainsi définir une relation d'ordre partielle sur l'ensemble des plans de production : un plan de production 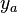 est meilleur qu'un plan
est meilleur qu'un plan 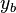 , noté
, noté 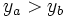 si et seulement si la valeur absolue des intrants de
si et seulement si la valeur absolue des intrants de 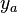 est inférieure (dont au moins un intrant strictement), soit la valeur absolue des extrants de
est inférieure (dont au moins un intrant strictement), soit la valeur absolue des extrants de 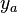 est supérieure (idem), soit les deux.
est supérieure (idem), soit les deux.
Un plan de production efficace est un plan de production tel qu'il n'existe aucun autre vecteur d'extrants nets meilleur que celui de ce plan de production.
L'ensemble de production est l'ensemble des plans de productions réalisables par un producteur donné.
Propriétés
On considère que les ensembles de productions économiques 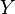 vérifient les propriétés suivants :
vérifient les propriétés suivants :
- l'ensemble de production est non-vide : il est possible au moins de ne rien produire,
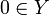
- monotonicité
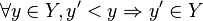
- divisibilité :
![\forall (y,\lambda), \lambda \in [0,1]\Rightarrow \lambda y\in Y](../i/m/e1d153a130b89b5b2b5c8c4e0bbcb41c.png)
- additivité :
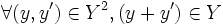 . Cette condition implique en particulier qu'il n'y a pas de difficulté à l'agrégation des ensembles de production.
. Cette condition implique en particulier qu'il n'y a pas de difficulté à l'agrégation des ensembles de production. - convexité :
![\forall (y,y',\alpha)\in Y^2\times[0,1], (\alpha y + (1-\alpha)y')\in Y](../i/m/e2171ed584cfdbbe0404b17e259f3eaf.png)
Sous ces hypothèses, on peut définir la fonction de production comme la frontière de l'ensemble de production.
Fonctions de productions
Voir aussi Fonction de production
Définition et propriétés
Par convention, on note 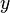 les extrants et
les extrants et  les intrants, sous forme de quantités positives. Cette forme de notation permet de définir des fonctions de production associées à un plan de production
les intrants, sous forme de quantités positives. Cette forme de notation permet de définir des fonctions de production associées à un plan de production 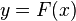 .
.
D'après ce qui précède, si l'ensemble de production Y est convexe, alors F est concave.
On suppose presque toujours que les fonctions de production néoclassiques sont soumises à des rendements marginaux décroissants, qui sont l'équivalent pour le producteur du goût pour la diversité du consommateur : 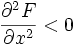
Taux et élasticité de substitution
la combinaison de plusieurs facteurs dans des proportions fixées permet a l'entrepreneur de réaliser un niveau de production donné. certains facteurs ont la faculté de pouvoir être utilisés a la place d'autres. la relation entre la quantité de facteur pouvant être utilisée a la place d'un autre est mesurée par le taux de substitution. L'élasticité quant à elle mesure la variation d'un facteur engendrée par la variation d'un autre élément
Isoquantes de production
Les isoquantes de production sont l'ensemble des combinaisons d'inputs permettant d'obtenir le même niveau d'output.
Si les fonctions de production sont concaves, les isoquantes de production sont convexes.
Taux marginal de substitution technique
Le taux marginal de substitution technique (TMST) de Y à X est le rapport positif entre la quantité y du facteur Y qu'il est possible d'abandonner et la quantité x de X qu'il est possible de lui substituer pour maintenir constant le niveau de production.
TMST = productivité marginale de X/productivité marginale de Y
Par analogie avec le taux marginal de substitution du consommateur, on définit le taux de substitution technique comme :
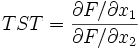
Le TMST est l'opposé de la pente des isoquantes de production (voir supra).
Rendements d'échelle
Une fonction de production présente des rendements d'échelle
- croissants si
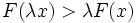 ;
; - décroissants si
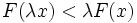 ;
; - constants si
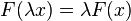 ;
;
Élasticité de substitution
l'élasticité de substitution mesure le taux de variation de la quantité d'un facteur X1 engendré par un certain taux de variation des prix relatifs des deux facteurs r1 et r2.
L'élasticité de substitution 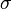 est une mesure de la courbure des isoquantes :
est une mesure de la courbure des isoquantes :
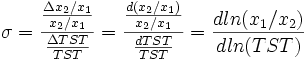
Programme primal : la maximisation du profit
On suppose que les producteurs sont preneurs de prix, et plus généralement on se place dans le cadre de la concurrence pure et parfaite.
En première approche, on considère que le producteur cherche à mesurer son profit 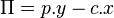 , où p et c sont respectivement le prix des extrants et le coût des intrants. L'ensemble des coûts de production pris en compte est très extensif, puisqu'il inclut la location des bâtiments, la rémunération de l'entrepreneur, la location du capital, etc.
, où p et c sont respectivement le prix des extrants et le coût des intrants. L'ensemble des coûts de production pris en compte est très extensif, puisqu'il inclut la location des bâtiments, la rémunération de l'entrepreneur, la location du capital, etc.
Le programme du producteur s'écrit donc :
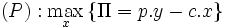 |
sous contrainte : 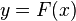 |
La résolution de ce programme se fait au moyen d'un Lagrangien :
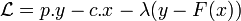
qui donne les conditions au premier ordre :
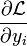 |
= | 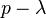 |
= | 0 |
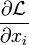 |
= | 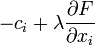 |
= | 0 |
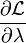 |
= | 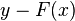 |
= | 0 |
On en tire la condition nécessaire d'optimalité :
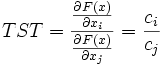
Il vient également :
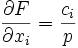
ce qui signifie que la productivité marginale est égale au coût réel.
On peut alors terminer la résolution du programme pour obtenir l'offre de la firme 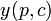 , les demandes de facteurs et le profit. Le lemme de Hotelling met en évidence une relation entre le premier et le dernier de ces facteurs:
, les demandes de facteurs et le profit. Le lemme de Hotelling met en évidence une relation entre le premier et le dernier de ces facteurs:
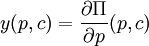 On démontre ce résultat par le théorème de l'enveloppe.
On démontre ce résultat par le théorème de l'enveloppe.
Sous les hypothèses ci-dessus, la fonction d'offre est homogène de degré zéro par rapport à 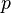 et
et  , et croissante par rapport à
, et croissante par rapport à 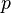 .
.
Pour les mêmes raisons, les demandes de facteurs sont aussi homogènes de degré zéro en 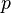 et
et  .
.
Programme dual : la minimisation des coûts
On peut voir le problème du producteur comme la maximisation du profit, ou inversement comme une minimisation de ses coûts de production. L'enjeu est alors de montrer que les deux programmes conduisent au même résultat en termes de niveau de production et de demande des facteurs, donc de profit.
Voir aussi
Liens internes
- Microéconomie
- Fonction de production
- Théorie du consommateur (micro-économie)
- Rendements d'échelle
Liens externes
- Théorie du producteur
- Comportement du consommateur et du producteur, notion de surplus et analyse des politiques publiques
- La théorie de la production et des coûts
- Portail de l’économie
