Système d'Anosov

Pour un article plus général, voir théorie du chaos.

En théorie des systèmes dynamiques, un système d'Anosov est un système hyperbolique, qui présente une dynamique extrêmement chaotique.

Cet article est une ébauche concernant l'analyse.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

Définition

Notion de système dynamique différentiel

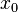Un système dynamique différentiel est défini par une application bijective $\phi_t : \Gamma \to \Gamma$ de l'espace des phases du système sur lui-même, telle qu'à une condition initiale $x_0$ soit associé un et un seul état futur à l'instant t (condition de déterminisme) :

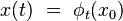x(t) \ = \ \phi_t(x_0)

Lorsque le temps t varie, cette bijection engendre un flot sur 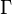$\Gamma$ , c’est-à-dire un groupe continu à un paramètre 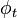$\phi_t$ tel que :

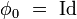\phi_0 \ = \ \mathrm{Id}

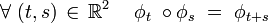\forall \ (t,s) \, \in \, \mathbb{R}^2 \, \quad \phi_t \ \circ \phi_s \ = \ \phi_{t+s}

Cette modélisation mathématique correspond par exemple au flot hamiltonien de la mécanique classique, ainsi qu'au flot géodésique sur une variété riemannienne.

La propriété d'hyperbolicité

L'hyperbolicité de l'espace des phases a été mise en évidence par Dmitri Anosov par analogie avec le flot géodésique de surfaces à courbure négative de la géométrie hyperbolique.

Typiquement pour un flot hamiltonien, l'hypersurface d'énergie constante 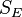$S_E$ de l'espace des phases admet presque partout une décomposition du type :

S_E \ = \ E_0 \ \oplus \ E_S \ \oplus \ E_I

où :

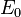$E_0$ est une variété à une dimension dans la direction du flot.
$E_S$ est le sous-espace des directions stables, directions perpendiculaires au flot. Pour une perturbation dirigée selon ces directions, il y a contraction exponentielle vers le futur, ce qui correspond à des exposants de Lyapounov négatifs (cette variété est donc instable vers le passé.)
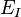$E_I$ est le sous-espace des directions instables, directions également perpendiculaires au flot. Pour une perturbation dirigée selon ces directions, il y a dilatation exponentielle vers le futur, ce qui correspond à des exposants de Lyapounov positifs (cette variété est donc stable vers le passé.).

Le fait qu'il existe nécessairement certaines directions contractantes complémentaires aux directions dilatantes peut être vu comme une conséquence du théorème de Liouville, qui dit que le flot hamiltonien préserve le volume dans l'espace des phases.

Pour un système chaotique dissipatif, il n'y a pas nécessairement de directions contractantes partout dans l'espace des phases, mais il existe en général au moins un sous-ensemble « attracteur » dans cet espace des phases sur lequel la dynamique est hyperbolique presque partout.

Bibliographie

(en) D. Anosov, « Geodesic flows on compact Riemannian manifolds of negative curvature », Proceedings of the Steklov Mathematical Institute, vol. 90, n^o 1, 1967, p. 1-235

Ouvrages d'initiation

John H. Hubbard et Beverly H. West, Équations différentielles et systèmes dynamiques, Cassini, 1999 (ISBN 978-2-84225015-7)
Grégoire Nicolis et Ilya Prigogine, À la rencontre du complexe, coll. « Philosophie d'aujourd'hui », PUF, 1992 (ISBN 978-2-13043606-5)
(en) Boris Hasselblatt (de) et Anatole Katok (de), A First Course in Dynamics with a Panorama of Recent Developments, Cambridge University Press, 2003 (ISBN 0-521-58750-6) [lire en ligne]
(en) Anatole Katok et Boris Hasselblatt, Introduction to the Modern Theory of Dynamical Systems, coll. « Encyclopedia of Mathematics and Its Applications » (n^o 54), Cambridge University Press, 1997 (ISBN 978-0-52157557-7) [lire en ligne]

Ouvrages plus techniques

(en) Stephen Smale, The mathematics of time - Essays on Dynamical Systems, Economic Processes & Related Topics, Springer-Verlag, 1980 (ISBN 978-0-387-90519-8)
(en) Boris Hasselblatt et Anatole Katok (eds.), Handbook of Dynamical Systems, Elsevier. Vol. 1A, 2002 (ISBN 978-0-444-82669-5) ; Vol. 1B, 2005 (ISBN 978-0-444-52055-5)
(en) Bernold Fiedler (de) (ed.), Handbook of Dynamical Systems. Vol. 2: Applications, Elsevier, 2002 (ISBN 978-0-444-50168-4) ; Vol. 3: Geometric Methods of Differentiable Dynamics, Elsevier, 2010 (ISBN 978-0-444-53141-4)
(en) Leonid Bunimovich (en), Roland Lwowitsch Dobruschin (de), Iakov Sinaï, Anatoly Vershik (de) et al., Dynamical Systems, Ergodic Theory and Applications, Series: Encyclopaedia of Mathematical Sciences 100, Volume package: Mathematical Physics, Springer-Verlag, 2^e édition, 2000 (ISBN 978-3-540-66316-4)

Bibliothèque virtuelle

Paul Manneville, Systèmes dynamiques et chaos, 1998, 233 pages [lire en ligne]
Cours donné par l'auteur (LadHyX, École Polytechnique) aux DEA de Physique des Liquides et de Mécanique.
(en) David Ruelle, « Ergodic theory of differentiable dynamical systems », Publ. Math. IHES, vol. 50, 1979, p. 27-58 [lire en ligne]

Portail de l’analyse
Portail de la physique

This article is issued from Wikipédia - version of the Saturday, March 22, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.