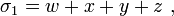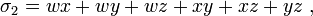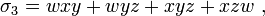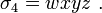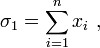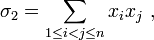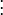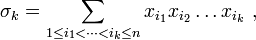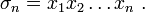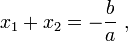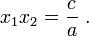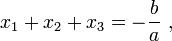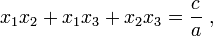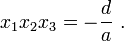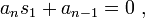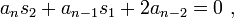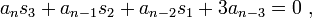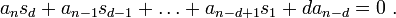Relations entre coefficients et racines
Un polynôme 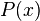 de degré
de degré 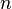 s'écrit sous sa forme la plus générale :
s'écrit sous sa forme la plus générale :
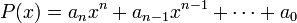
où 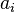 est appelé coefficient de
est appelé coefficient de 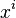 .
On peut aussi définir
.
On peut aussi définir  grâce à ses racines, c'est-à-dire l'ensemble des valeurs de
grâce à ses racines, c'est-à-dire l'ensemble des valeurs de  qui annulent
qui annulent  . Le théorème de d'Alembert-Gauss nous assure que tout polynôme de degré
. Le théorème de d'Alembert-Gauss nous assure que tout polynôme de degré 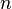 admet exactement
admet exactement 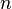 racines sur
racines sur 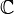 , éventuellement multiples (sur
, éventuellement multiples (sur 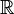 en revanche, ce n'est pas toujours vrai). On montre que
en revanche, ce n'est pas toujours vrai). On montre que  peut se réécrire :
peut se réécrire :
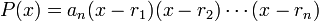
avec 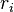 les racines de
les racines de  , éventuellement multiples. Les relations entre les coefficients et les racines portent le nom de François Viète, le premier à les avoir énoncées dans le cas de racines positives.
, éventuellement multiples. Les relations entre les coefficients et les racines portent le nom de François Viète, le premier à les avoir énoncées dans le cas de racines positives.
Relations de Viète
Polynômes symétriques
On définit le 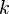 -ième polynôme symétrique, noté
-ième polynôme symétrique, noté 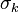 , comme la somme de ses éléments multipliés
, comme la somme de ses éléments multipliés 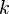 fois. Par exemple, les polynômes symétriques associés aux variables
fois. Par exemple, les polynômes symétriques associés aux variables 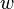 ,
,  ,
, 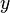 et
et 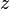 sont :
sont :
Plus généralement,
Théorème
Soient  un polynôme défini comme ci-dessus et
un polynôme défini comme ci-dessus et 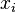 les
les 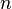 racines de
racines de  , éventuellement multiples. Nous avons le résultat suivant :
, éventuellement multiples. Nous avons le résultat suivant :
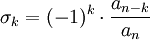
Exemples
- Cas
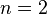 . Soient
. Soient 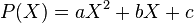 et
et 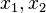 ses racines. Alors,
ses racines. Alors,
- Cas
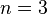 . Soient
. Soient 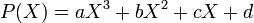 et
et 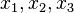 ses racines. Alors,
ses racines. Alors,
Sommes de Newton
Exemple introductif
On se donne le polynôme 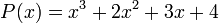 avec
avec 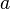 ,
, 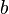 ,
,  ses racines. On veut déterminer la somme
ses racines. On veut déterminer la somme 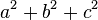 . Pour cela, nous disposons de l'identité suivante :
. Pour cela, nous disposons de l'identité suivante :
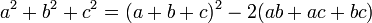
Si bien que, d'après les relations de Viète :
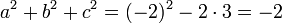
Théorème
Les sommes de Newton sont une généralisation de ce principe. On pose 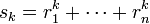 , où les
, où les 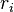 sont les racines de
sont les racines de 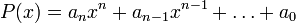 . (En particulier,
. (En particulier, 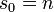 ). La méthode présentée dans l'exemple se généralise, mais les calculs deviennent compliqués. On peut par contre démontrer directement[1] :
). La méthode présentée dans l'exemple se généralise, mais les calculs deviennent compliqués. On peut par contre démontrer directement[1] :
Note et référence
- ↑ Pellet, « Expression de la somme des puissances semblables des racines d'une équation, en fonction des coefficients », Nouvelles annales de mathématiques, 2e série, vol. 14, , p. 259-265 (lire en ligne)
- Portail de l’algèbre