Régression (statistiques)
Pour les articles homonymes, voir Régression.La régression est un ensemble de méthodes statistiques très utilisées pour analyser la relation d'une variable par rapport à une ou plusieurs autres.
Pendant longtemps, la régression d'une variable aléatoire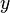 
sur le vecteur de variables aléatoires 
désignait la moyenne conditionnelle de 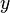sachant . Aujourd'hui, le terme de régression désigne tout élément de la distribution conditionnelle de 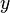sachant considérée comme une fonction de . On peut par exemple s'intéresser à la moyenne conditionnelle, à la médiane conditionnelle, au mode conditionnel, à la variance conditionnelle[1]...
Le terme « régression » a été introduit par Francis Galton à la suite d'une étude sur la taille des descendants de personnes de grande taille, qui diminue de générations en générations vers une taille moyenne (donc leur taille régresse)[2],[3].
En apprentissage automatique, on distingue les problèmes de régression des problèmes de classification. Ainsi, on considère que les problèmes de prédiction d'une variable quantitative sont des problèmes de régression tandis que les problèmes de prédiction d'une variable qualitative sont des problèmes de classification. Certaines méthodes, comme la régression logistique, sont à la fois des méthodes de régression au sens où il s'agit de prédire la probabilité d'appartenir à chacune des classes et des méthodes de classification[4].
Principaux modèles de régression
Le modèle de régression le plus connu est le modèle de régression linéaire.
Lorsque le modèle n'est pas linéaire, on peut effectuer une régression approchée par des algorithmes itératifs, on parle de régression non linéaire.
Si on s'intéresse au quantile conditionnel de la distribution de la variable aléatoire y sachant le vecteur de variables aléatoires x, on utilise un modèle de régression quantile[5],[6].
Si la variable expliquée est une variable aléatoire binomiale, il est courant d'utiliser une régression logistique ou un modèle probit.
Si la forme fonctionnelle de la régression est inconnue, on peut utiliser un modèle de régression non paramétrique.
Voir aussi
- Régression linéaire
- Régression linéaire multiple
- Régression polynomiale
- Régression logistique
- Modèle linéaire généralisé
- Régression non paramétrique
- Modèles de régression multiple postulés et non postulés
- Régression circulaire
- Régression elliptique
- Régression locale
Références
- ↑ Manski 1991
- ↑ (en) Robert G. Mogull, Second-Semester Applied Statistics, Kendall/Hunt Publishing Company, (ISBN 0-7575-1181-3), p. 59
- ↑ Galton 1989
- ↑ James et al. 2013, p. 28
- ↑ (en) Roger Koenker et G. Bassett, « Regression quantiles », Econometrica, , p. 33-50
- ↑ (en) Roger Koenker, Quantile Regression, Cambridge University Press,
Bibliographie
- (en) Francis Galton, « Kinship and Correlation (reprinted 1989) », Statistical Science, Institute of Mathematical Statistics, vol. 4, no 2, , p. 80–86 (DOI 10.1214/ss/1177012581, JSTOR 2245330)
- (en) Charles Manski, « Regression », Journal of Economic Literature, vol. 29, no 1, , p. 34-50 (lire en ligne)
- Gareth James, Daniela Witten, Trevor Hastie et Robert Tibshirani, An Introduction to Statistical Learning, Springer Verlag, coll. « Springer Texts in Statistics »,
Portail de l’économie 
Portail des probabilités et de la statistique