Réfractomètre à réflexion totale interne

Cet article est une ébauche concernant l’optique. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

Cet article a une forme trop académique. La forme ressemble trop à un extrait de cours et nécessite une réécriture afin de correspondre aux standards de Wikipédia. N'hésitez pas à l'améliorer.

Le principe du réfractomètre utilisé en gemmologie est basé sur le phénomène de réflexion totale interne (RTI). Ce principe aide à mesurer l’indice de réfraction d’une gemme.

Mais tout d’abord un rappel sur la réfraction. Observons deux milieux :

l’air (milieu n1) et une gemme λ (milieu n2). Un rayon lumineux incident traverse l’air à la vitesse de la lumière, rencontre la surface de la gemme λ, entre dans le milieu de la gemme et est automatiquement ralenti et réfracté (il est dévié).

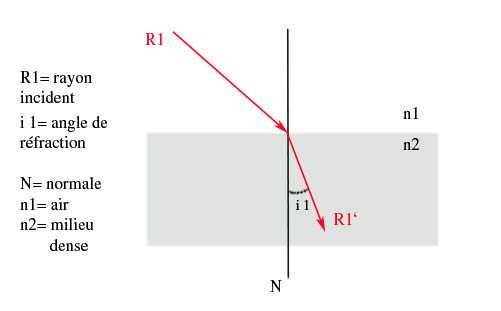
Notre but : calculer le ratio entre la vitesse de la lumière dans l’air et la vitesse de la lumière dans la gemme, véritable indice de réfraction de la gemme.

Vitesse de la lumière air/Vitesse de la lumière gemme = Indice de réfraction gemme

Ce calcul étant très compliqué, il peut se substituer à un autre calcul plus simple : La mesure de l’angle i lorsque le rayon incident est dévié à l’intérieur du matériau.

Le réfractomètre est capable de nous donner cette mesure grâce à la RTI.

Principe de la Réflexion Totale Interne dans un réfractomètre utilisé en gemmologie.

Définition : On obtient une RTI lorsque le rayon lumineux incident atteint l’interface entre les deux milieux (n1 et n2) de densité optique différente à un angle supérieur à l’angle critique. Le rayon lumineux n’est plus réfracté vers l’autre milieu (n1) mais reste à l’intérieur du milieu (n2) le plus dense.

Application : Dans le cas du Réfractomètre à RTI, les deux milieux utilisés sont :

Un verre très dense optiquement (n2) (Indice de réfraction 1,96) et la gemme λ (n1).

Le verre dense, taillé et poli sous forme d’hémicylindre, possède un fort pouvoir de dispersion, c’est pour cela que la lumière incidente utilisée est une lumière monochromatique jaune émettant à 589 nanomètres, auquel cas la lumière blanche serait dispersée dans les couleurs du spectre, c’est-à-dire un arc-en-ciel., d’où un indice illisible.

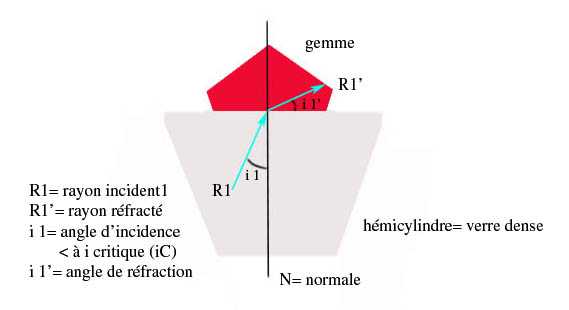
La lumière incidente traversant l’hémicylindre (n2) atteint l’interface entre les deux milieux à un certain angle. Selon les propriétés des gemmes, les angles critiques à partir desquels il y aura une RTI seront différents. Lorsque le rayon incident (R1) atteint la surface entre les deux milieux à un angle inférieur à l’angle critique (iC), il est réfracté (R1’) dans la gemme et sera en quelque sorte « perdu ».

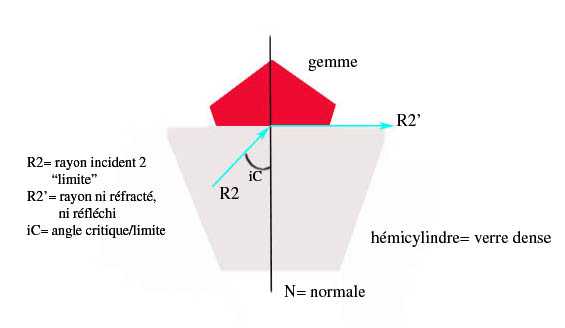
Lorsque le rayon incident (R2) atteint la surface entre les 2 milieux à l’angle critique (iC), il n’est ni réfracté ni réfléchi (R2’) à l’intérieur mais va suivre l’interface entre les deux milieux.

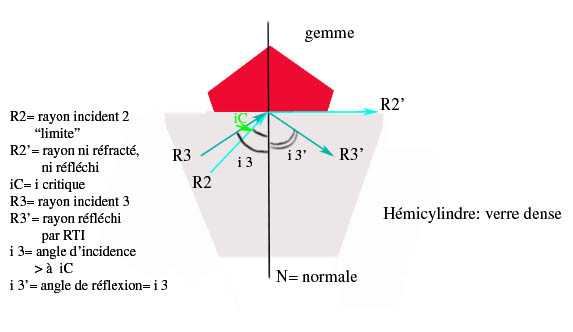
Lorsque le rayon incident (R3) atteint la même surface à un angle supérieur à l’angle critique (iC), il se réfléchit (R3’) à l’intérieur de l’hémicylindre avec le même angle que l’angle d’incidence.

Que voit-on DANS le réfractomètre à RTI ?

Sur une échelle graduée située à l’intérieur du réfractomètre apparaissent deux zones : Une zone claire correspondant aux rayons qui auront subi la RTI, et une zone sombre correspondant aux rayons réfractés, « perdus ». La limite entre les deux zones correspond à l’angle critique (iC) et indique l’indice de réfraction de la gemme testée.

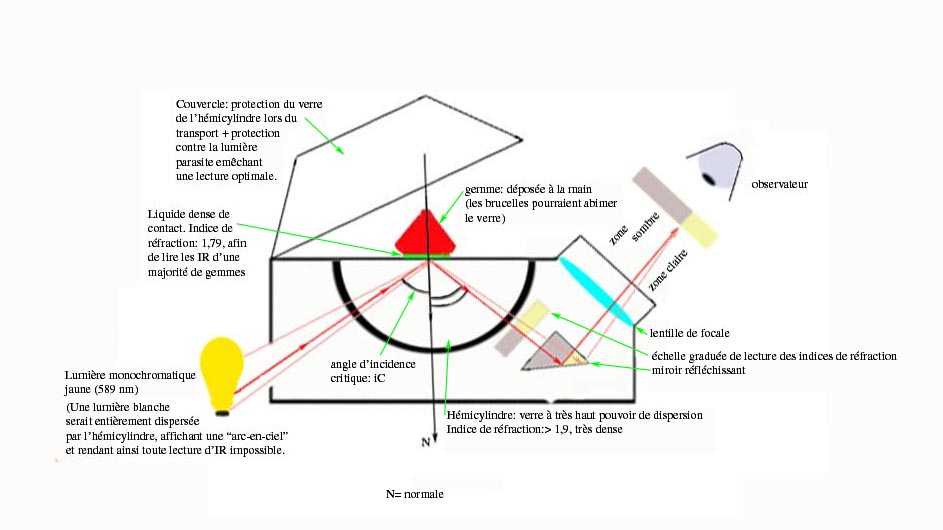
Conditions d’utilisation : Afin de faciliter l’adhérence entre les deux milieux, on utilise un liquide de contact, le iodure de méthylène, qui possède un indice de réfraction de 1,79 environ. Tous les matériaux qui sont au-delà de cet indice sont qualifiés d’OTL (Over the limit/ hors limite) et restent donc illisibles (diamant/ certains grenats/ zircon/ moissanite…).

La gemme doit être idéalement bien taillée, les surface lisses, sans aspérités et préférablement planes (voir ci-dessous pour la lecture au point). Elle peut être transparente, translucide ou opaque.

Un matériau brut, s’il présente des faces de prismes ou de pyramides ou autre, suffisamment lisses, peut également être testé.

Un seul indice de réfraction peut nous informer sur 3 choses :

-il s’agit d’un matériau cristallisé isotrope donc monoréfringent appartenant au système cubique (ex : grenat, fluorite)

-il s’agit d’un matériau amorphe donc isotrope. (ex : opale, verre, ambre/attention le liquide de contact peut endommager ce matériau…)

-cas n°3, voir plus bas.

Cas des matériaux biréfringents :

Biréfringence

Deux indices de réfractions signifient que le rayon incident entrant dans la gemme a été non seulement dévié mais divisé en deux rayons à direction de vibration perpendiculaire et vitesse et propagation différente.

ex. : tous les matériaux non-isotropes. S’ils sont cristallisés, ils n’appartiennent pas au système cubique. MAIS : si la lecture se fait le long de l’axe optique de ces matériaux, alors un seul indice de Réfraction sera lisible (cas n° 3).

Interprétation des lectures :

Un seul IR : voir ci-dessus/ l'indice est immobile

Deux IR :

Un fixe et un variable si l’on fait tourner le matériau à 360° autour de lui-même sur le verre de l’hémicylindre : le matériau est Uniaxe (Si l’indice minimum varie : il est Uniaxe négatif/ si l’indice maximum varie, il est uniaxe positif)

Les deux indices bougent : le matériau est biaxe. (Si l’indice minimum varie le plus : il est biaxe négatif/ si l’indice maximum varie le plus : il est biaxe positif)

Lecture au point : Cas des gemmes taillées en cabochons ou en perles ou autres surface non planes : C’est une lecture approximative

Filtre polarisant : Il est préférable de faire une première lecture sans filtre polarisant puis d'utiliser le filtre pour affiner la lecture. Dans le cas des matériaux biréfringents, la lecture des indices de réfraction sera alternée lorsqu'on fera tourner le filtre polarisant sur la focale.

Articles connexes

• Optique
• Biréfringence
• Réfraction
• Réfractométrie

• Portail de la physique