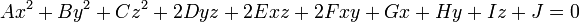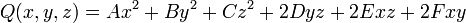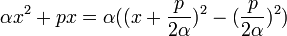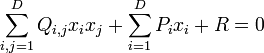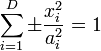Quadrique

Cet article est une ébauche concernant les mathématiques.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

Quadriques non dégénérées en dimension 3. De gauche à droite : hyperboloïdes à une et deux nappes, ellipsoïde, paraboloïde hyperbolique, cylindre, paraboloïde elliptique et cône.

En mathématiques, et plus précisément en géométrie euclidienne, une quadrique, ou surface quadratique, est une surface de l'espace euclidien de dimension 3, lieu des points vérifiant une équation cartésienne de degré 2

Ax^2+By^2+Cz^2+2Dyz+2Exz+2Fxy+Gx+Hy+Iz+J=0

les coefficients A à J étant réels, avec A,B,C,D,E,F non tous nuls.

Plus généralement, on peut considérer les quadriques dans le cadre des espaces affines, de dimension 3 ou plus. Ce sont alors des hypersurfaces, lieu d'annulation (en) d'un polynôme de degré 2. On peut également les étudier dans le cadre de la géométrie projective, qui simplifie et unifie complètement les résultats. On peut enfin prendre un autre corps de base que celui des réels.

Classification

Présentation des principales quadriques

Les quadriques non dégénérées^[1] sont décrites ci-dessous à partir de leurs équations réduites dans un repère orthonormé convenable.

L'ellipsoïde	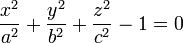$\frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2}-1 = 0 \,$ ,
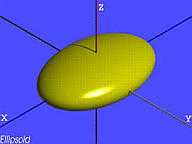L'hyperboloïde à une nappe (H1)	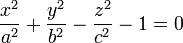$\frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2}-1 = 0 \,$ ,
L'hyperboloïde à deux nappes (H2)	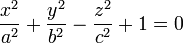$\frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} +1 = 0 \,$ ,
Le paraboloïde elliptique (PE)	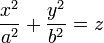$\frac{x^2}{a^2} + \frac{y^2}{b^2} =z \,$ ,
Le paraboloïde hyperbolique (PH)	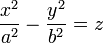$\frac{x^2}{a^2} - \frac{y^2}{b^2} = z \,$ ,
Le cône à base elliptique	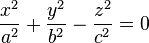$\frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} = 0 \,$ ,
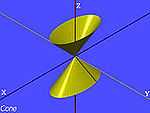Le cylindre elliptique	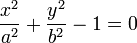$\frac{x^2}{a^2} + \frac{y^2}{b^2}-1 = 0 \,$ ,
Le cylindre hyperbolique	$\frac{x^2}{a^2} -\frac{y^2}{b^2}-1 = 0 \,$ ,
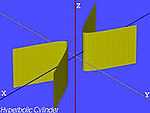Le cylindre parabolique	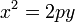$\displaystyle{x^2 = 2 p y}$ .

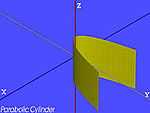Classification générale

L'équation de la surface peut s'écrire :

Q(x,y,z)+Gx+Hy+Iz+J=0~

où Q désigne la forme quadratique

Q(x,y,z)=Ax^2+By^2+Cz^2+2Dyz+2Exz+2Fxy~

de matrice :

M_Q=\begin{pmatrix} A & F & E \\ F & B & D \\ E & D & C\end{pmatrix}

dont les valeurs propres sont toutes réelles puisque cette matrice est symétrique réelle.

La signature de la forme quadratique est le couple (p,q) où p est le nombre de valeurs propres strictement positives de Q et q le nombre de valeurs propres strictement négatives. Le rang de Q est alors p+q. Par définition d'une quadrique, le rang de Q ne peut être nul. Le fait que la signature d'une forme quadratique ne dépende pas du choix de la base choisie est démontré par la loi d'inertie de Sylvester.

Lorsque le rang est égal à 3, la quadrique admet un centre de symétrie.

Rang	Signature	Quadrique non dégénérée	Quadrique dégénérée
3	(3,0) ou (0,3)	ellipsoïde	$\varnothing$ ou point
3	(2,1) ou (1,2)	hyperboloïde à 1 ou 2 nappes ou cône
2	(2,0) ou (0,2)	paraboloïde elliptique ou cylindre elliptique	$\varnothing$ ou droite
2	(1,1)	paraboloïde hyperbolique ou cylindre hyperbolique	réunion de deux plans
1	(1,0) ou (0,1)	cylindre parabolique	$\varnothing$ ou plan ou réunion de deux plans

Démonstration

Pour simplifier, les coordonnées seront toujours notées x, y et z, après les différents changements de repères orthonormés qui vont suivre.

La matrice de la forme quadratique, de valeurs propres notées 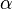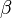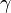$\alpha~$ , $\beta~$ , $\gamma~$ , est diagonalisable à l'aide d'une matrice de passage orthogonale. Dans un nouveau repère orthonormé, l'équation de la surface s'écrit

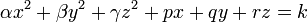\alpha x^2 + \beta y^2 + \gamma z^2 + p x + q y + r z = k~

Lorsqu'une des valeurs propres est non nulle, par exemple 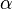$\alpha~$ , il est possible de centrer la coordonnée correspondante:

\alpha x^2 + p x = \alpha ((x + \frac{p}{2 \alpha} )^2 - ( \frac{p}{2 \alpha} )^2)

ce qui revient à effectuer une translation ou un changement d'origine du repère.

Lorsque le rang est égal à trois, les trois valeurs propres sont non nulles; dans un nouveau repère orthonormé, l'équation devient:

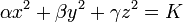\alpha x^2 + \beta y^2 + \gamma z^2 = K~

- si la signature vaut (3,0) ou (0,3), les trois valeurs propres ont même signe. Si K est nul, il s'agit d'un point; sinon, il s'agit d'un ellipsoïde si K a le signe des valeurs propres, et de l'ensemble vide sinon.
- si la signature vaut (2,1) ou (1,2), deux valeurs propres ont même signe, que l'on dira ici majoritaire; si K est nul, il s'agit d'un cône; sinon, il s'agit d'un hyperboloïde à une nappe si K a le signe majoritaire, d'un hyperboloïde à deux nappes sinon.

Lorsque le rang est égal à deux, l'une des valeurs propres est nulle, et une seule, par exemple 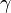$\gamma~$ ; dans un nouveau repère orthonormé, l'équation devient:

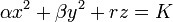\alpha x^2 + \beta y^2 + r z = K~

- si r est non nul, on obtient un paraboloïde elliptique si les deux valeurs propres non nulles sont de même signe, et un paraboloïde hyperbolique sinon, car l'équation s'écrit:

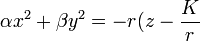\alpha x^2 + \beta y^2 = - r (z - \frac{K}{r}

- si r est nul, et si K est nul, il s'agit de la réunion de deux plans si les valeurs propres non nulles sont de signe opposé, et d'une droite sinon;
- si r est nul et K non nul, il s'agit d'un cylindre hyperbolique si les valeurs propres non nulles sont de signe contraire, et sinon, d'un cylindre elliptique lorsque K est du signe des valeurs propres non nulles, et l'ensemble vide sinon.

Lorsque le rang est égal à un, une seule valeur propre est non nulle, par exemple 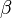$\beta~$ ; dans un nouveau repère orthonormé, l'équation devient:

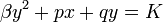\beta y^2 + p x + q y = K~~

puis après un dernier changement de repère orthonormé

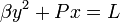\beta y^2 + P x = L~~

Si P est nul, on obtient un plan si L est nul, et la réunion de deux plans ou l'ensemble vide, selon que L est du signe de 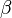$\beta$ ou non. Sinon, il s'agit d'un cylindre parabolique.

Quadrique en dimension quelconque

Plus généralement, dans un espace de dimension D, si les coordonnées de l'espace sont 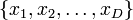$\{x_1, x_2, \dots, x_D\}$ , la quadrique générale est une hypersurface définie par l'équation algébrique :

\sum_{i,j=1}^D Q_{i,j} x_i x_j + \sum_{i=1}^D P_i x_i + R = 0

pour un choix spécifique de Q, P et R.

L'équation normalisée pour une quadrique non dégénérée centrée à l'origine est de la forme :

\sum_{i=1}^D \pm {x_i^2 \over a_i^2} =1

Applications

En modélisation d'image

Pour une surface d'équation 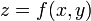$z=f(x,y)~$ , la formule de Taylor-Young fournit une approximation locale de la surface par la quadrique d'équation:

p (x-a) + q (y-b) + \frac{1}{2} [r (x-a)^2 + 2 s (x-a)(y-b) + t (y-b)^2 ]

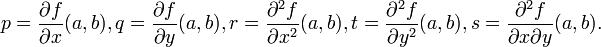
avec les notations dites de Monge $p= \frac{\partial f}{\partial x}(a,b) , q= \frac{\partial f}{\partial y}(a,b) , r= \frac{\partial^2 f}{\partial x^2}(a,b), t= \frac{\partial^2 f}{\partial y^2}(a,b), s= \frac{\partial^2 f}{\partial x \partial y}(a,b).$

Cette approximation locale est exploitée en modélisation d'images ^[2], où elle fournit des résultats intéressants^[3].

Notes et références

↑ Non vides, réduites à un point, ou produit de plans.
↑ Sylvie Philipp, Modélisation structurale de la texture. Extraction du grain primaire et de sa règle de placement dans Douzième colloque Gretsi, Juan-les-Pins, 1988, Lire en ligne, p. 590.
↑ Alaa Mustafa, Contribution à l'étude des courbures discrètes et de leurs applications, 2008 [Thèse].

Voir aussi

Conique

Portail de la géométrie

This article is issued from Wikipédia - version of the Friday, July 10, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.