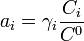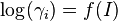Force ionique

La force ionique, notée I (ou F_I de manière à la distinguer de l'intensité), est un des principaux facteurs influençant l'activité des ions en solution aqueuse. Elle s'exprime en mol·L^-1 et est calculée de la manière suivante :

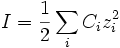
I=\frac{1}{2} \sum_{i} C_i z_i^2\,\!

où C_i représente la concentration molaire de l'ion i et z_i sa charge.

Mesure de la force ionique

La meilleure solution pour déterminer la force ionique consiste à déterminer les concentrations respectives des différents ions en solution et à utiliser la formule précédente. Cependant on peut aussi se contenter d'une estimation de la force ionique connaissant la concentration totale en solides dissous (notée TDS et exprimée en mg·L^-1) ou la conductivité électrique (notée SpC et exprimée en 10^-6 S·cm^-1) de la solution. Ces estimations utilisent les formules empiriques suivantes :

I = 2,5 x 10^-5 TDS ^{[réf. nécessaire]}
I= 1,7 x 10^-5 SpC ^{[réf. nécessaire]}

Force ionique et activité chimique

Une solution idéale est une solution où les interactions entre toute paire de particules (molécules ou ions) sont identiques, de la même façon que l'on définit un gaz parfait comme un gaz dans lequel il n'existe pas d'interactions entre molécules. Les électrolytes réels ne suivent qu'imparfaitement les relations établies pour les solutions idéales et ce d'autant moins que les concentrations sont élevées. Cet écart à l'idéalité est lié aux interactions d'origine électrique entre les ions. Ainsi est-on amené à introduire des coefficients d'activité qui corrigent les concentrations (coefficient d'activité : <1 ; égale à 1 si la solution est idéale). On définit ainsi l'activité par :

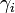a_i = \gamma_i \frac{C_i}{C^0}

où $\gamma_i~$ est le coefficient d'activité de l'espèce i, 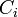$C_i~$ sa concentration dans la solution, exprimée en mol·L^-1 et C₀ la concentration de référence égale à 1 mol/L.

Les coefficients d'activité se déduisent alors de I par une relation du type :

\log (\gamma_i) = f( I ) \!

La fonction 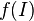$f(I)\!$ est variable suivant les auteurs et le domaine d'application (valeur de la force ionique).

Formules courantes

Plusieurs relations semi-empiriques permettent d'obtenir le coefficient d'activité moyen d'un électrolyte (ex : NaCl, MgSO₄, …) ou le coefficient d'activité d'un ion (ex : Na⁺, Cl^-, …) en solution à partir de la valeur de la force ionique I.

Les trois formules les plus courantes sont détaillées ci-dessous (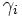 $\gamma_i\,\!$ est le coefficient d'activité de l'ion i, 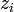$z_i\,\!$ son nombre de charges et 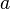$a$ un paramètre homogène à une longueur), les deux premières sont basées sur la théorie de Debye-Hückel :

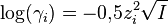
Formule de Debye-Hückel limite (DHL) : $\log (\gamma_i) = - 0{,}5 z_i^2 \sqrt{I}\,\!$
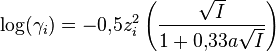
Formule de Debye-Hückel étendue (DHE) : $\log (\gamma_i) = - 0{,}5 z_i^2 \left ( \frac{\sqrt{I}}{1 + 0{,}33 a \sqrt{I}} \right ) \,\!$
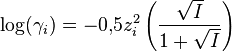
Approximation de Güntelberg (AG) : $\log (\gamma_i) = - 0{,}5 z_i^2 \left ( \frac{\sqrt{I}}{1 + \sqrt{I}} \right ) \,\!$

La formule (DHL) n'est valable que si la force ionique I est inférieure à 10^-2,3 mol·L^-1 car elle considère chaque ion comme une charge ponctuelle. Cette approximation ne peut plus être faite pour une solution concentrée. Les formules (DHE) et (AG) ne sont quant à elles valables que si I est inférieure à 0,1 mol·L^-1.

D'autres formules ou théories plus complexes ont donc été développées pour mettre en relation le coefficient d'activité et la force ionique lorsque I est supérieure à 0,1 mol·L^-1. C'est notamment le cas de l'équation de Davies, du modèle de Pitzer ou de la théorie SIT.

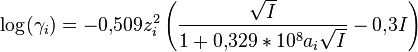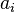Loi de Davies pour l'eau à 298 K et I<0,5 M : $\log (\gamma_i) = - 0{,}509 z_i^2 \left ( \frac{\sqrt{I}}{1 + 0{,}329*10^8 a_i \sqrt{I}} - 0{,}3 I \right ) \,\!$ où $a_i$ est le diamètre effectif moyen des ions hydratés et I la force ionique.

Articles connexes

Activité chimique
Longueur de Debye
Potentiel chimique

Portail de la chimie

This article is issued from Wikipédia - version of the Friday, July 17, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Force ionique

Mesure de la force ionique

Force ionique et activité chimique

Formules courantes

Articles connexes

Medical Encyclopedia