Fonction de hachage

On nomme fonction de hachage, de l'anglais hash function (hash : pagaille, désorde, recouper et mélanger) par analogie avec la cuisine, une fonction particulière qui, à partir d'une donnée fournie en entrée, calcule une empreinte servant à identifier rapidement, bien qu'incomplètement, la donnée initiale. Les fonctions de hachage sont utilisées en informatique et en cryptographie.

Exemple de fonction de hachage appliquée sur 3 entrées distinctes.

Principe général

Une fonction de hachage est typiquement une fonction qui pour un ensemble de très grande taille (théoriquement infini) et de nature très diversifiée va renvoyer des résultats aux spécifications précises (en général des chaînes de caractère de taille limitée ou fixe) optimisées pour des applications particulières. Les chaînes permettent d'établir des relations (égalité, égalité probable, non-égalité, ordre...) entre les objets de départ sans accéder directement à ces derniers, en général soit pour des questions d'optimisation (la taille des objets de départ nuit aux performances), soit pour des questions de confidentialité.

Terminologie

Le résultat d'une fonction de hachage peut être appelé selon le contexte somme de contrôle, empreinte, empreinte numérique^[1], hash, résumé de message, condensé, condensat ou encore empreinte cryptographique lorsque l'on utilise une fonction de hachage cryptographique.

Collision

Article détaillé : Collision (informatique).

Est appelé « collision » d'une fonction de hachage, un couple de données de son ensemble de départ distinctes, qui sont telles que leur somme de contrôle est identique.

Considérations mathématiques

Définitions

Soit une fonction de hachage f d'un ensemble S dans un ensemble N.

f est dite parfaite pour l'ensemble S si elle est une injection de S dans N.

f est dite minimale si elle est parfaite et S et N sont de même cardinal.

Dans le cas S=N, f est dite préservant une relation donnée 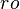$ro$ de S si

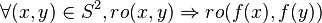
$\forall (x,y) \in S^2, ro(x,y) \Rightarrow ro(f(x),f(y))$

Conséquences

Une fonction de hachage parfaite ne possède aucune collision.

Lorsque l'ensemble d'arrivée est de cardinal inférieur à l'ensemble de départ, il existe nécessairement des collisions. Le nombre de collisions est alors supérieur ou égal à card(S)-card(N) (la démonstration s'appuie sur le principe des tiroirs).

Applications en optimisation

Principes généraux

Les fonctions de hachage servent à rendre plus rapide l'identification des données : calculer l'empreinte d'une donnée ne doit coûter qu'un temps négligeable. Une fonction de hachage doit par ailleurs éviter autant que possible les collisions (états dans lesquels des données différentes ont une empreinte identique) : dans le cas des tables de hachage, ou de traitements automatisés, les collisions empêchent la différenciation des données ou, au mieux, ralentissent le processus.

Hors cryptographie, les fonctions de hachage ne sont en général pas injectives, car on souhaite conserver des empreintes plus petites que les données traitées – pour des considérations de stockage en mémoire : il faut donc concevoir une fonction de hachage homogène, donnant une empreinte de taille raisonnable tout en minimisant le nombre de collisions. Par exemple on peut associer une empreinte de 16, 32 ou 64 bits à chaque document d'une bibliothèque de plusieurs millions de fichiers. Si deux fichiers ont des empreintes différentes, ils sont à coup sûr différents. Si leurs empreintes sont identiques en revanche, l'identité n'est pas encore prouvée ; mais la comparaison octet par octet n'aura plus à se faire que sur le sous-ensemble bien plus restreint de fichiers qui ont la même empreinte.

Selon l'emploi de la fonction de hachage, il est souhaitable qu'un infime changement de la donnée en entrée (inversion d'un seul bit, par exemple) entraine une perturbation importante de l'empreinte correspondante, rendant une recherche inverse par approximations successives impossible : on parle d'effet avalanche.

Conception d'une fonction de hachage

La conception d'une fonction de hachage est en général heuristique. Pour des cas d'optimisation le concepteur cherchera à trouver un compromis entre la taille des empreintes et le nombre de collisions pour des échantillons de données traités représentatifs de cas d'utilisation réels.

La question du hachage uniforme, ou encore de l'équirépartition de l'ensemble de départ vis-à-vis de la fonction de hachage est un élément essentiel conditionnant l'efficacité de la fonction de hachage: si par exemple, dans une table de hachage de taille 10, nous devons ranger des éléments numérotés de 10 en 10, ou de 20 en 20, il est totalement inopportun d'utiliser la fonction modulo 10, car alors tous les éléments se retrouveraient groupés dans la première case. La difficulté de trouver une "bonne" fonction de hachage consiste donc à trouver une fonction h qui "catégorise" notre ensemble de départ S en classes d'équivalence de proportions égales, pour la relation d'équivalence 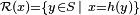$\scriptstyle{ \mathcal R (x) = \{ y \in S \,|\ x = h(y) \}}$ . 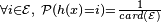De façon probabiliste, une fonction de hachage uniforme dans l'ensemble d'arrivée $\scriptstyle \mathcal E$ est une fonction $\scriptstyle h$ telle que $\scriptstyle{\mathcal 8 i\mathcal{2E,~P}(h(x)=i) = \frac{1}{card(\mathcal E)}}$ . On parlera dans ce cas d'uniformité de la sortie.

Exemple pédagogique simple

Un exemple courant de fonction de hachage passable peut par exemple être la fonction qui renvoie la taille d'un fichier informatique.

Nous voulons comparer deux fichiers informatiques afin de déterminer s'ils sont identiques (par exemple déterminer si un document a été modifié). La solution évidente consiste à vérifier la correspondance caractère par caractère mais cette méthode peut s'avérer fastidieuse. Une solution souvent plus rapide consiste à comparer la taille des fichiers dans la mémoire (en général disponible immédiatement dans l'OS, employée ici comme empreinte ou hachage) : si cette taille diffère nous avons obtenu très rapidement la preuve que les deux fichiers étaient différents. A contrario, si les deux tailles de fichiers coïncident, il n'est pas possible de conclure formellement que les deux fichiers sont identiques.

Exemples d'applications typiques

Tables de hachage et structures de données

On utilise fréquemment les fonctions de hachage dans des structures de données : les tables de hachage. Le principe est d'utiliser les empreintes des clés comme index des « cases » de la table. Ces empreintes sont des nombres entiers obtenus en hachant la « clé » des objets à stocker, souvent une chaîne de caractères. On peut ensuite retrouver un objet à partir de sa clé: il suffit de lire dans le tableau la case dont l'index est l'empreinte de cette clé. Toutefois, des collisions existent car il existe moins d'empreintes possibles que de valeurs possibles pour la clé. Des techniques destinées à lever ces conflits sont nécessaires, par exemple le principe de chaînage : chaque case de la table constitue le début d'une liste chaînée. Si deux clés fournissent le même condensé et donc accèdent à la même portion de la table, on doit alors parcourir la liste chaînée pour l'élément qui correspond bien à la clé donnée (la clé est en général stockée avec l'élément dans un nœud de la liste).

Fonction de hachage perceptuelle

La plupart des fonctions de hachage produisent des empreintes radicalement différentes si l'entrée est légèrement modifiée. Ce phénomène est particulièrement visible avec les fonctions de hachage cryptographiques qui se comportent de manière imprévisible grâce à l'effet avalanche. Toutefois, il existe des fonctions de hachage qui tolèrent une certaine marge d'erreur. Elles sont particulièrement utiles pour hacher des données qui peuvent subir des perturbations comme les sons ou encore les images. Par exemple, un fichier audio original et sa version en MP3 seront totalement différents si la comparaison se fait au niveau binaire. Toutefois, le résultat est plus ou moins identique pour un auditeur. Un système développé par Philips^[2] consiste à subdiviser le signal en plusieurs bandes de fréquences et à les hacher séparément. La fonction de hachage est conçue pour ne modifier que quelques bits si le signal change. En calculant la distance de Hamming entre deux signatures, il est possible de savoir si deux échantillons correspondent à la même séquence sonore.

Ces techniques, alliées au tatouage numérique, sont principalement destinées à lutter contre la contrefaçon. Elles sont également intéressantes pour gérer des bases de données et trouver rapidement des échantillons présentant de fortes similitudes.

Somme de contrôle

Article détaillé : Somme de contrôle.

Table de hachage

Article détaillé : Table de hachage.

Applications en cryptographie

Principes généraux

En cryptographie les contraintes sont plus exigeantes et la taille des empreintes est généralement bien plus longue que celle des données initiales ; un mot de passe dépasse rarement une longueur de 8 caractères, mais son empreinte peut atteindre une longueur de plus de 100 caractères. La priorité principale est de protéger l'empreinte contre une attaque par force brute, le temps de calcul de l'empreinte passant au second plan.

Une fonction de hachage cryptographique est utilisée entre autres pour la signature électronique, et rend également possibles des mécanismes d'authentification par mot de passe sans stockage de ce dernier. Elle doit être résistante aux collisions, c’est-à-dire que deux messages distincts doivent avoir très peu de chances de produire la même signature. De par sa nature, tout algorithme de hachage possède des collisions, mais on considère le hachage comme cryptographique si les conditions suivantes sont remplies :

il est très difficile de trouver le contenu du message à partir de la signature (attaque sur la première préimage)
à partir d'un message donné, de sa signature et du code source de la fonction de hachage, il est très difficile de générer un autre message qui donne la même signature (attaque sur la seconde préimage)
il est très difficile de trouver deux messages aléatoires qui donnent la même signature (résistance aux collisions)

Par très difficile, on entend « techniquement impossible en pratique », par toutes techniques algorithmiques et matérielles, en un temps raisonnable. Le MD5 par exemple n'est plus considéré comme sûr car on a trouvé deux messages qui génèrent la même empreinte. Toutefois, la mise en œuvre de ces techniques n'est pas aisée et dans le cas du MD5, les chercheurs ont trouvé une collision sur deux messages au contenu aléatoire. On peut cependant construire à partir d'une collision des attaques réelles^[3].

Exemples d'applications typiques

Contrôle d'accès

Un mot de passe ne doit pas être stocké en clair sur une machine pour des raisons de sécurité. Seul le résultat du hachage du mot de passe est donc stocké. Pour identifier un utilisateur, l'ordinateur compare l'empreinte du mot de passe d'origine (stocké) avec l'empreinte du mot de passe demandé. Toutefois, cette manière de faire n'est pas complètement satisfaisante. Si deux utilisateurs décident d'utiliser le même mot de passe alors le condensé obtenu sera identique. Cette faille est potentiellement utilisable par trois méthodes :

attaque par dictionnaire
attaque par force brute
attaque par table arc-en-ciel

Lors d'une attaque par dictionnaire, on pourrait raisonnablement déduire que le mot de passe choisi par les deux utilisateurs est relativement facile à mémoriser.

Pour contrer ce type d'attaque, on ajoute une composante aléatoire lors de la génération initiale de l'empreinte. Cette composante, aussi appelée « sel », est souvent stockée en clair. On peut simplement utiliser l'heure de l'attribution du mot de passe ou un compteur qui varie selon l'utilisateur. Le mot de passe est ensuite mélangé avec le sel, cette étape varie selon le système employé. Une méthode simple est de concaténer le mot de passe avec le sel. Le sel n'étant pas identique pour deux utilisateurs, on obtiendra deux signatures différentes avec le même mot de passe. Cela réduit fortement la marge d'une attaque via un dictionnaire.

Les algorithmes SHA-1 (Secure Hash Algorithm 1 : 160 bits) et MD5 (Message-Digest algorithm 5, 128 bits, plus ancien et moins sûr) sont des fonctions de hachage utilisées fréquemment. Le SHA-2 (SHA-256, SHA-384 ou SHA-512 bits au choix) est d'ores et déjà prêt s'il faut abandonner aussi le SHA-1.

Salage

Article détaillé : Salage_(cryptographie).

Le salage (salting en anglais) consiste à ajouter une chaîne de caractères à l'information avant le hachage. Par exemple, dans un cadre cryptographique, au lieu de pratiquer le hachage sur le mot de passe seul, on peut le faire sur le résultat de la concaténation du mot de passe avec une autre chaîne de caractères pseudo-aléatoire, obtenue par un hachage de l'identifiant (login) concaténé avec le mot de passe. Les deux fonctions de hachage (celle qu'on utilise pour générer la chaîne pseudo-aléatoire et celle qu'on applique au résultat) peuvent être différentes (par exemple SHA-1 et MD5).

Cela permet de renforcer la sécurité de cette fonction.

En effet, en l'absence de salage, il est possible de cracker le système à l'aide de tables de hachage correspondant à des valeurs (telles que des mots de passe) souvent utilisées, par exemple les tables arc-en-ciel.

Le simple ajout d'un sel avant hachage rend l'utilisation de ces tables caduque, et le craquage doit faire appel à des méthodes telles que l'attaque par force brute (cette méthode, consistant à tester toutes les valeurs possibles, prend tellement de temps avec un bon mot de passe que l'on ne peut plus qualifier cela de crackage).

Notes et références

↑ Office québécois de la langue française, « Fiche terminologique : empreinte numérique »,‎ 2005.
↑ Robust Audio Hashing for Content Identification (2001) Jaap Haitsma, Ton Kalker and Job Oostveen, Philips Research, International Workshop on Content-Based Multimedia Indexing (CBMI'01)
↑ (en) Ondrej Mikle Practical Attacks on Digital Signatures Using MD5 Message Digest

Annexes

Liens externes

(fr) Applet Java
Hash Générateur Autre produit Générateur de hashs en ligne, avec beaucoup de hachage comme md2, md4, md5, sha1, snefru, ripemd, haval, mysql323,lanman, tiger, etc. Environ 118 différents algorithmes.

Portail de la cryptologie
Portail de l'informatique théorique

This article is issued from Wikipédia - version of the Tuesday, October 20, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Fonction de hachage

Principe général

Terminologie

Collision

Considérations mathématiques

Définitions

Conséquences

Applications en optimisation

Principes généraux

Conception d'une fonction de hachage

Exemple pédagogique simple

Exemples d'applications typiques

Tables de hachage et structures de données

Fonction de hachage perceptuelle

Somme de contrôle

Table de hachage

Applications en cryptographie

Principes généraux

Exemples d'applications typiques

Contrôle d'accès

Salage

Notes et références

Annexes

Liens externes

Medical Encyclopedia