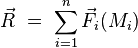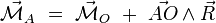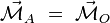Couple (physique)
Le couple est un concept fondamental de la mécanique, domaine de la physique qui étudie les mouvements et les déformations des systèmes. Un couple appliqué à un système provoque une variation de son moment cinétique sans modifier le mouvement de son centre de gravité[1].
En d'autres termes, on appelle couple tout ensemble d'actions mécaniques dont la résultante sur le système 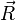 est nulle et le moment résultant
est nulle et le moment résultant 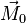 par rapport à un point
par rapport à un point 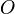 est non nul. Ce moment est alors indépendant du point
est non nul. Ce moment est alors indépendant du point 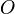 .
.
Un couple est l'effort en rotation appliqué à un axe. Il est ainsi nommé en raison de la façon caractéristique dont on obtient ce type d'action : un bras qui tire, un bras qui pousse, les deux forces étant égales et opposées.
Conventions et unités

On représente un couple par une flèche (semblable à celle qui représente un vecteur) dans l'axe de rotation, s'éloignant de l'objet pour une rotation dans le sens trigonométrique (qui est l'inverse du sens des aiguilles d'une montre), comme la vitesse de rotation.
On mesure le couple en newtons-mètres (N·m). Un couple de 1 N·m appliqué à un axe représente un apport d'énergie de 1 joule (J) par radian, soit 2π J par tour. Un couple est homogène à un travail ou une énergie (en joules), mais il est préférable, pour éviter les confusions, d'exprimer cette grandeur dans l'unité qui rappelle comment elle est définie[2].
| Grandeur | unité | Grandeur | unité | |
|---|---|---|---|---|
| force F | N | couple C | N·m | |
| masse m | kg | moment d'inertie I | kg·m² | |
| vitesse v | m/s | vitesse angulaire ω | rad/s | |
| quantité de mouvement m·v | kg·m/s | moment angulaire I·ω | kg·m²·rad/s | |
| énergie cinétique E = 1/2 m·v² | joules | énergie cinétique E = 1/2 I·ω² | joules | |
| puissance P = F·v | watts | puissance P = C·ω | watts | |
| accélération a = F/m | m/s² | accélération angulaire α = C/I | rad/s² |
Dans des documents historiques on peut rencontrer le dyne·cm valant 10-7 N·m, le kg.m valant 9,80665 N·m, et dans des documents utilisant des unités de mesure anglo-saxonnes, des ounce·inch valant 7,06·10-3 N·m, des pound·foot valant 1,35 N·m, pounds·inch valant 0,13 N·m[3].
Propriété fondamentale du couple
Moment d'une force
Le moment d'une force F, par rapport à un point O, dont le point d'application est au point M, est défini par :
Un théorème général
Supposons le système d'actions mécaniques représentable par un ensemble dénombrable de forces 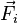 où l'indice
où l'indice 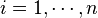 . Pour ce système d'actions mécaniques, le moment résultant est :
. Pour ce système d'actions mécaniques, le moment résultant est :
Calculons alors le moment résultant par rapport à un autre point A :
On écrit que chaque vecteur position se décompose comme suit :
d'où le moment résultant :
La seconde somme représente le moment résultant en O. De plus, dans la première somme, le vecteur 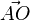 est indépendant de l'indice i ; on peut donc le sortir de la somme et écrire :
est indépendant de l'indice i ; on peut donc le sortir de la somme et écrire :
La somme qui apparait n'est autre que la résultante des forces :
d'où le théorème général :
Cas particulier du couple
Le couple étant un système d'actions mécaniques dont la résultante 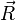 est nulle, son moment résultant est indépendant du point choisi pour le calculer :
est nulle, son moment résultant est indépendant du point choisi pour le calculer :
On utilise souvent la notation 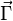 pour représenter le moment résultant d'un couple. Compte tenu du résultat précédent, il n'est en effet pas nécessaire de préciser le point choisi pour calculer le moment.
pour représenter le moment résultant d'un couple. Compte tenu du résultat précédent, il n'est en effet pas nécessaire de préciser le point choisi pour calculer le moment.
Représentations d'un couple
Il existe une infinité de représentations différentes d'un même couple 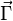 donné.
donné.
Représentation la plus simple
La plus simple, qui lui donne son nom, consiste à considérer un ensemble de deux forces :
- l'une,
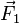 , appliqué en un point
, appliqué en un point 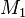 différent de l'origine
différent de l'origine 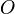 fixée.
fixée.
- l'autre,
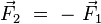 , appliqué en un point
, appliqué en un point 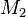 symétrique du point
symétrique du point 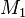 par rapport à l'origine
par rapport à l'origine 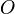 .
.
Ainsi, la résultante 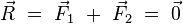 est bien nulle. On suppose de plus que les vecteurs
est bien nulle. On suppose de plus que les vecteurs 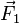 et
et 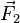 ne sont pas colinéaires au vecteur
ne sont pas colinéaires au vecteur 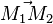 ; le cas le plus simple consiste à prendre les deux forces perpendiculaires à ce vecteur :
; le cas le plus simple consiste à prendre les deux forces perpendiculaires à ce vecteur :

Si on note la distance 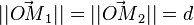 , la norme des forces
, la norme des forces 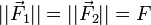 , et
, et 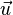 le vecteur unitaire perpendiculaire au plan de la figure, le couple vaut explicitement :
le vecteur unitaire perpendiculaire au plan de la figure, le couple vaut explicitement :
Exemples d'autres représentations
On peut représenter le même couple 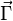 que dans l'exemple précédent par d'autres ensembles d'actions mécaniques. Par exemple, par deux forces :
que dans l'exemple précédent par d'autres ensembles d'actions mécaniques. Par exemple, par deux forces :
- l'une,
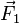 , appliquée au point
, appliquée au point 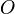 .
.
- l'autre,
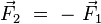 , appliquée en un point
, appliquée en un point 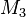 situé à une distance non nulle de l'origine
situé à une distance non nulle de l'origine 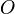 .
.
Ainsi, la résultante 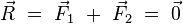 est toujours nulle. Pour simplifier, on peut encore supposer que les vecteurs
est toujours nulle. Pour simplifier, on peut encore supposer que les vecteurs 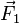 et
et 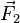 sont perpendiculaires au vecteur
sont perpendiculaires au vecteur 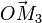 :
:

Pour retrouver la même valeur du couple : 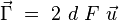 , il suffit de prendre par exemple une combinaison du type :
, il suffit de prendre par exemple une combinaison du type :
-
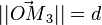 et :
et : 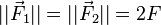
- ou :
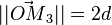 et :
et : 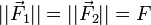
Il existe une infinité de représentations possibles ...
- Précession
- Lorsque le couple ne s'exerce pas rigoureusement dans l'axe, il se produit une rotation de cet axe appelée précession[réf. nécessaire].
Voir aussi
Bibliographie
Articles connexes
- Travail
- Moment (mécanique)
- Pseudovecteur
- Torseur
Lien externe
- (histoire des sciences) La mise en évidence de la notion de couple par Poinsot (1803), en ligne et commenté sur BibNum.
Notes et références
- ↑ Richard Taillet, Loïc Villain et Pascal Febvre, Dictionnaire de physique, Bruxelles, De Boeck, , p. 154.
- ↑ BIPM, Brochure sur le système international d'unités (lire en ligne), p. 30.
- ↑ (en) « Guide for the Use of the International System of Units (SI) ».
- Portail de la physique
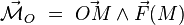
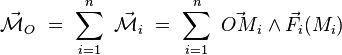
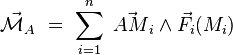
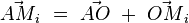
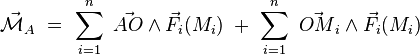
![\sum_{i=1}^n \vec{AO} \wedge \vec{F}_i(M_i) \ = \ \vec{AO} \wedge \left[ \sum_{i=1}^n \vec{F}_i(M_i) \right]](../i/m/bb29e98498ae54aada6b8c696c6950f2.png)