Caustique

Pour les articles homonymes, voir Caustique (homonymie).

Cet article est une ébauche concernant l’optique et la géométrie.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

Lorsqu'une onde plane est réfléchie par un miroir parabolique, tous les rayons convergent en un seul point.

Lorsqu'une onde plane est réfléchie par un miroir circulaire, tous les rayons ne convergent pas en un seul point : ils forment une caustique.

Une caustique désigne en optique et en mathématiques l'enveloppe des rayons lumineux subissant une réflexion ou une réfraction sur une surface ou une courbe.

Plus spécifiquement, on parle de caustique au flambeau lorsque les rayons lumineux sont issus d'un point à distance finie et de caustique au soleil si la source lumineuse se trouve à une distance infinie.

Une caustique par réflexion est aussi appelée catacaustique, tandis qu'une caustique par réfraction est appelée diacaustique.

En astronomie, des caustiques sont associées aux mirages gravitationnels^[1].

Étymologie et histoire

Cette courbe peut se voir, dans la vie de tous les jours, par exemple à la surface du café au lait dans une tasse éclairée de façon oblique. Ici, il s'agit, non pas d'une cardioïde, mais d'un arc de néphroïde.

Le physicien allemand Ehrenfried Walther von Tschirnhaus consacra sa vie à l'optique géométrique et à la fabrication de lentilles et miroirs à l'usage de l'astronomie. C'est dans ce cadre qu'il étudia en 1682 les caustiques par réflexion. Il choisit le terme « caustique » en référence au mot grec kaustikos provenant de katein (brûler).

Il prouva en outre que les caustiques des courbes algébriques sont rectifiables : on peut calculer analytiquement leur longueur, sur un intervalle donné, par le calcul intégral.

Le concept de caustique fut également étudié par Jacques Bernoulli, le Marquis de l'Hôpital et La Hire.

Anticaustique ou caustique secondaire

Pour construire une caustique, il peut être utile de se servir d'une courbe auxiliaire appelée anticaustique ou caustique secondaire. C'est la développante de la caustique. Autrement dit, la caustique est la développée de sa caustique secondaire, c'est-à-dire le lieu des centres de courbure de la caustique secondaire..

Dans le cas de la caustique par réflexion d'une courbe 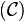$(\mathcal C)$ pour une source S, la caustique secondaire est l'orthotomique de la courbe par rapport à S, c'est-à-dire le lieu des symétriques de S par rapport aux tangentes à la courbe 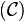$(\mathcal C)$ ^[2].

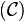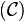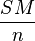Dans le cas de la caustique par réfraction d'indice n d'une courbe $(\mathcal C)$ pour une source S, la caustique secondaire est l'enveloppe des cercles^[3] de centres M appartenant à la courbe $(\mathcal C)$ et de rayons $\frac{SM}{n}$ .

Notes et références

Références

↑ « Simulateur de mirages gravitationnels », sur ulg.ac.be
↑ cf. Caustique sur Mathcurve
↑ cf. Anticaustique sur Mathcurve

Liens internes

Cusp
Cardioïde

Liens externes

Robert Ferreol et Jacques Mandonnet, « Caustique », sur Encyclopédie des formes mathématiques remarquables,‎ 2012 (consulté le 17 mai 2015)
Robert Ferreol et Jacques Mandonnet, « Anticaustique », sur Encyclopédie des formes mathématiques remarquables,‎ 2000 (consulté le 17 mai 2015)
(fr) Des caustiques dans la vie quotidienne

Portail de l’optique
Portail de la géométrie

This article is issued from Wikipédia - version of the Friday, September 25, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.