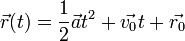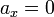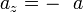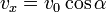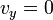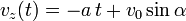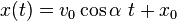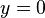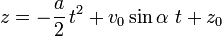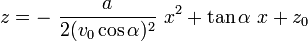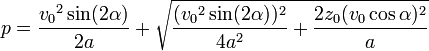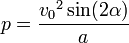Balistique

La balistique est la science qui a pour objet l'étude du mouvement des projectiles.

Domaines d'étude

On distingue^[1]^, ^[2] :

la balistique intérieure, dont l'objet est l'ensemble des phénomènes se produisant à l'intérieur du canon (mouvement du projectile, détente des gaz...)^[3]. Voir chapitre 6.1 de l'article Balistique judiciaire.
la balistique extérieure, dont l'objet est le mouvement d'un projectile à l'extérieur du canon. À courte portée, on peut ignorer la courbure du sol et utiliser la formulation décrite plus bas. Cependant la description de la trajectoire d'un missile balistique à longue portée exige une correction tenant compte de la courbure terrestre^[4].
la balistique terminale, dont l'objet est l'étude du projectile lorsqu'il frappe la cible (comportement différent selon les types de tirs : tirs à « bout touchant », à « bout portant » - à moins de 50 cm - et à « longue distance »). Voir chapitre 6.3 de l'article Balistique judiciaire.

Approche mathématique de la balistique extérieure

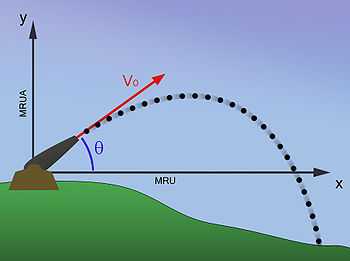
La balistique est l'étude d'un objet au voisinage du sol^[5]. L'objet subit alors trois forces, son poids 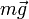$m\vec{g}$ , la poussée d'Archimède 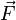$\vec{F}$ et le frottement de l'air $\vec{f}$ .

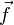Si on peut négliger le frottement de l'air (vitesse faible de l'objet), on a un cas particulier d'un mouvement uniformément accéléré (MUA), car l'accélération 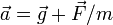$\vec{a} = \vec{g} + \vec{F}/m$ est constante.

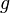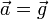Si la poussée d'Archimède est négligeable (objet de densité très supérieure à celle de l'air), l'accélération est alors égale à celle de la pesanteur, exprimée par la constante $g$ orientée vers le bas : $\vec{a} = \vec{g}$ .

Si on étudie le mouvement d'un objet à la surface d'une planète sans atmosphère, il n'y a ni poussée d'Archimède, ni frottement de l'air et 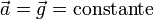$\vec{a} = \vec{g} = \mbox{constante}$ pour toute vitesse initiale à condition que l'altitude et la distance parcourue soient très inférieures au rayon de la planète, sinon 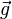$\vec{g}$ n'est plus constant et la trajectoire n'est plus parabolique, mais elliptique : le projectile a alors la trajectoire d'un satellite.

Si 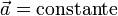$\vec{a} = \mbox{constante}$ , et si 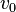$v_0$ est la vitesse initiale, faisant un angle 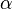$\alpha$ par rapport à l'horizontale, la position 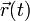$\vec{r}(t)$ à l'instant t est.

\vec{r}(t) = \frac{1}{2} \vec{a} t^2+\vec{v_0}t+\vec{r_0}

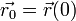
avec $\vec{r_0} = \vec{r}(0)$

Dans un repère orthonormé (Oxyz), orienté en sorte que (Oz) soit vertical vers le haut, et (Oy) perpendiculaire à 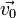$\vec{v_0}$ , on a alors (a > 0) :

\ \ a_x = 0

\ \ a_y = 0

\ \ a_z =-\ \ a

puis :

\ \ v_x = v_0 \cos \alpha

\ \ v_y = 0

\ \ v_z(t) =- a \,t + v_0 \sin\alpha

puis, en intégrant par rapport à 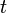$t$ :

\ \ x(t) = v_0 \cos\alpha~t + x_0

\ \ y = 0

z =- \frac{a}{2}\,t^2 + v_0 \sin\alpha~t + z_0

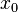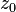où $x_0$ et $z_0$ sont les positions initiales de l'objet dans le repère orthonormé (Oxyz).

La trajectoire parabolique correspondante dans le plan xz est alors :

z =-\ \frac{a}{2 (v_0 \cos\alpha)^2 }~x^2 + \tan\alpha~x + z_0

La portée atteinte par le projectile à l'horizontale s'exprime par ( ici il ne s'agit pas de vecteurs ) :

p = \frac{{v_0}^2 \sin(2\alpha)}{2a} + \sqrt{\frac{({v_0}^2 \sin(2\alpha))^2}{4a^2}+ \frac{2z_0(v_0 \cos\alpha)^2}{a}}

Si $z_0 = 0$ :

p = \frac{{v_0}^2 \sin(2\alpha)}{a}

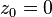On voit que, pour une portée p cherchée, deux valeurs complémentaires de 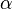$\alpha$ donnent une solution s'il y en a. La plus grande (supérieure à 45°), donne un tir vertical, l'autre un tir plongeant.

L'altitude maximale atteinte par le projectile est 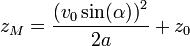$z_M = \frac{{(v_0 \sin(\alpha))}^2}{2a} + z_0$ .

Notes et références

↑ http://www.larmurier.net/Balistique.htm
↑ http://prof.denocq.chez-alice.fr/01_5eme/08_projets/2007-2008/7-Balistique.htm
↑ http://fred.elie.free.fr/balistique_interieure.htm
↑ la phase de balistique extérieure est parfois divisée en deux : la phase de stabilisation du projectile juste après sa sortie du canon appelé balistique de transition (ou intermédiaire), et le reste du vol toujours appelé balistique extérieure.
↑ http://gilbert.gastebois.pagesperso-orange.fr/java/balistique/theorie_balistique.htm

Voir aussi

Liens externes

balistique sur wiktionnaire
Pendule balistique
Balistique aux XVIe et XVIIIe. Autour des travaux de Bélidor (pdf)
Simulation de trajectoires par Gilbert Gastebois

Portail de la physique

This article is issued from Wikipédia - version of the Friday, October 02, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.