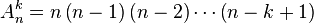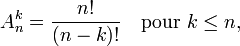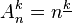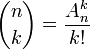Arrangement
En mathématiques, l'arrangement fait partie de l'analyse de dénombrement (ou combinatoire) et est utilisée, entre autres, dans le calcul de probabilité.
Lorsque nous choisissons k objets parmi n objets et que l’ordre dans lequel les objets sont sélectionnés revêt une importance, nous pouvons les représenter par un k-uplet d'éléments distincts et on en constitue une liste ordonnée sans répétition possible, c'est-à-dire dans laquelle l'ordre des éléments est pris en compte (si l'on permute deux éléments de la liste, on a une liste différente, et un élément ne peut être présent qu'une seule fois).
Une telle liste ordonnée est appelée un arrangement.
Le nombre d'arrangements que l'on peut faire est noté 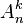 et vaut :
et vaut :
Cette formule peut se comprendre à l'aide d'un arbre des choix successifs, puisque le premier élément est choisi parmi n, le second parmi (n – 1)… et le dernier parmi (n – k + 1).
Avec la notation factorielle, où n! = 1×2×…×n, cette formule devient
tandis que 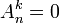 pour k > n (ce qui exprime le principe des tiroirs).
Il s’agit en fait simplement de la factorielle décroissante appliquée aux seuls entiers naturels :
pour k > n (ce qui exprime le principe des tiroirs).
Il s’agit en fait simplement de la factorielle décroissante appliquée aux seuls entiers naturels :
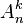 est en fait le nombre d'injections que l'on peut faire
d'un ensemble à k éléments vers un ensemble à n éléments.
Le nombre d'arrangements est lié au coefficient binomial
est en fait le nombre d'injections que l'on peut faire
d'un ensemble à k éléments vers un ensemble à n éléments.
Le nombre d'arrangements est lié au coefficient binomial  (anciennement
(anciennement 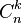 ) par :
) par :
Exemples
Exemple d'énumération d'éléments par arrangement
Soit un ensemble de 4 éléments E = {a, b, c, d}. Les arrangements sans répétition de 3 éléments choisis parmi les 4 éléments de E sont :

Il y en a 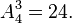
Exemple de dénombrement pour n grand
À un examen, cinq candidats tirent les uns après les autres un sujet dans une urne contenant des questions toutes différentes. Le premier tirage se fera sur un ensemble de 50 questions possibles. À chaque tirage suivant, la question qui vient d'être tirée est enlevée de l'urne. Ainsi, en faisant passer les cinq candidats, le tirage se fait d'abord sur 50, puis sur 49, et ainsi de suite jusqu'à 46 qui représente l'ensemble des questions restantes dans l'urne pour le dernier tirage. Le nombre d'arrangements pour cette série de 5 questions prises parmi 50 est alors de 50 × 49 × 48 × 47 × 46.
Si on remettait la question tirée de nouveau dans l'urne à chaque tirage, ce serait un arrangement avec répétition de 5 (k) parmi 50 (n), et la solution vaudrait 505.
Exemples d'arrangements :
- une phrase sans répétition de mot est un arrangement du dictionnaire ;
- une association forme son bureau (président, trésorier, secrétaire) à partir des membres de l'association ; le bureau est un arrangement de l'association ;
- le podium d'une course est un arrangement de l'ensemble des participants.
Définition mathématique
Définition :
Soient E un ensemble fini de cardinal n et k un entier naturel. Un k-arrangement sans répétition de E est une application injective de {1, 2, ..., k} dans E.
Autre définition :
Soient E un ensemble fini de cardinal n et k un entier naturel. Un k-arrangement de E (ou k-arrangement sans répétition de E, ou encore arrangement sans répétition de n éléments pris k à k) est un k-uplet (a1, a2, ..., ak) d'éléments de E tel que ai ≠ aj quel que soit i, j ∈ [1, k] avec i ≠ j. Un tel k-uplet est aussi appelé k-liste distincte d'éléments de E.
Théorème
Soient E et F deux ensembles finis de cardinaux respectifs n et k. L’ensemble 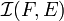 des applications injectives de F dans E est fini et son cardinal est égal à n(n – 1)... (n – k + 1) si k ≤ n et 0 sinon. Ce cardinal se note
des applications injectives de F dans E est fini et son cardinal est égal à n(n – 1)... (n – k + 1) si k ≤ n et 0 sinon. Ce cardinal se note 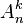 et se lit « Ank ».
On dit aussi qu'on a un arrangement de k à n.
et se lit « Ank ».
On dit aussi qu'on a un arrangement de k à n.
- Si k > n, alors il n'existe aucune injection de F dans E et donc
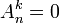 .
. - Si k < n, alors démontrons l'égalité par récurrence sur l'entier k.
- Si k = 1 alors F est un singleton et toute application de F dans E est injective donc
 .
. - Supposons l'égalité vérifiée pour tout ensemble F de cardinal k - 1 (2 ≤ k ≤ n) et démontrons la au rang k :
Soit F un ensemble de cardinal k, et x un élément de F. Posons G=F\{x}. Nous avons card(G)=k-1.
Considérons la relation qui relie deux injections de F dans E quand elles ont même restriction à G. Les classes d'équivalence partitionnent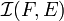 en classes ayant toutes comme cardinal n-(k-1). En effet, il y a autant de façons de prolonger une injection de G dans E en une injection de F dans E que de choix de l'image de x parmi les n-k+1 images possibles. De plus le nombre de classes d'équivalence est égal au nombre de restrictions différentes d'applications de
en classes ayant toutes comme cardinal n-(k-1). En effet, il y a autant de façons de prolonger une injection de G dans E en une injection de F dans E que de choix de l'image de x parmi les n-k+1 images possibles. De plus le nombre de classes d'équivalence est égal au nombre de restrictions différentes d'applications de 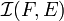 à G; il y en a donc
à G; il y en a donc 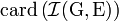 (la restriction d'une injection à une partie étant injective). D'après le lemme des bergers :
(la restriction d'une injection à une partie étant injective). D'après le lemme des bergers : .
.
- Si k = 1 alors F est un singleton et toute application de F dans E est injective donc
- Si k=0, nous poserons par convention pour tout entier naturel n
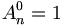 , puisqu'il existe une seule application qui va de l'ensemble vide ∅ dans un ensemble quelconque E qui de plus est injective !
, puisqu'il existe une seule application qui va de l'ensemble vide ∅ dans un ensemble quelconque E qui de plus est injective !
Démonstration (élémentaire)
Si 1 ≤ k ≤ n alors supposons que F={x1, x2, ..., xk}. Pour construire une application injective de F dans E, nous devons
- choisir l'image de x1 et il y a n images possibles,
- choisir l'image de x2 et il reste n-1 images possibles,
- ...
- choisir l'image de xk, il reste dans l'ensemble E n - (k-1) éléments non atteints donc n - (k-1) images possibles.
Au total, nous avons construit n.(n-1).....(n - k + 1) applications injectives différentes.
Corollaire
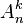 est aussi le nombre de k-arrangements sans répétition d'un ensemble E de cardinal n et nous avons
est aussi le nombre de k-arrangements sans répétition d'un ensemble E de cardinal n et nous avons 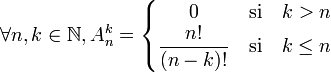
Démonstration :
Supposons F={x1, x2, ..., xk}. Une injection f de F dans E s'identifie au k-uplet d'éléments distincts (f(x1), f(x2), ..., f(xk)). Il y a donc une bijection entre l'ensemble des applications injectives de F dans E et l'ensemble des k-uplets d'éléments distincts de E.
Remarque :
Construire un arrangement revient à placer les uns après les autres, k objets discernables pris parmi n, dans k cases numérotées et donc une permutation de n éléments est un n-arrangement de n éléments. La notion d'arrangement généralise donc celle de permutation.
Articles connexes
- Arrangement avec répétition
- Combinaison (mathématiques)
- Combinaison avec répétition
- Permutation
- Permutation avec répétition
- Portail des mathématiques