Algèbre graduée

Cet article est une ébauche concernant l'algèbre.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

Pour les articles homonymes, voir Algèbre (homonymie).

En mathématiques, en algèbre linéaire, on appelle algèbre graduée une algèbre dotée d'une structure supplémentaire, appelée graduation.

Définition

Soit A une algèbre sur un corps (ou plus généralement sur un anneau) K. Une graduation sur A est la donnée d’une famille de sous-espaces vectoriels $(A_i)_{i\in\N}$ de A vérifiant :

$A = \bigoplus_{i\in\N}A_i$
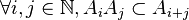$\forall i,j\in\N,A_iA_j\subset A_{i+j}$ , et donc $\forall \left[ i,j\in\N,x \in A_i, y \in A_j \right], \ \ x \times y \in A_{i+j}$ .

L’algèbre A est alors dite graduée (parfois ℕ-graduée, comme cas particulier de la notion d'algèbre M-graduée pour un monoïde M^[1]).

Les éléments de A_i sont dits homogènes de degré i. Un idéal est dit homogène si, pour chaque élément a qu'il contient, il contient également les parties homogènes de a. Cela revient à dire que I est engendré par des éléments homogènes.

Tout anneau (non gradué) A peut être doté d'une graduation en posant A₀ = A et A_i = 0 pour tout i > 0. Cette structure est appelée graduation triviale de A.

Une application $f$ entre des algèbres graduées A et B (sur le même corps) est un homomorphisme d'algèbres graduées^[1] si 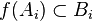$f(A_i)\subset B_i$ pour tout i.

Exemples

L'anneau de polynômes en plusieurs indéterminées K[X₁, … , X_n], où les éléments homogènes de degré n sont les polynômes homogènes de degré n.
L'algèbre tensorielle T(V) sur un espace vectoriel V, où les éléments homogènes de degré n sont les tenseurs de la forme $v_1\otimes v_2\otimes\dots\otimes v_n$ .
L'algèbre symétrique (en) S(V) et l'algèbre extérieure Λ(V) sont des algèbres graduées, les éléments homogènes de degré n étant les images des éléments homogènes de T(V). Plus généralement, si un idéal I d'une algèbre graduée A est homogène, le quotient A/I est naturellement gradué par $(A/I)_i=A_i/(I\cap A_i).$

Notes et références

1 2 N. Bourbaki, Algèbre (lire en ligne), p. III.30.

Article connexe

Algèbre différentielle graduée (en)

Portail de l’algèbre

This article is issued from Wikipédia - version of the Wednesday, September 23, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Algèbre graduée

Définition

Exemples

Notes et références

Article connexe

Medical Encyclopedia