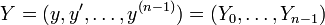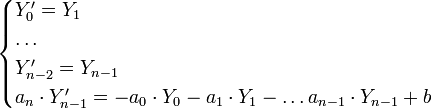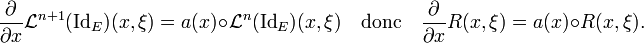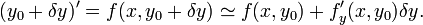Équation différentielle linéaire
|
|
Cet article est une ébauche concernant l'analyse. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
|
Une équation différentielle linéaire est un cas particulier d'équation différentielle pour lequel on peut appliquer des procédés de superposition de solutions, et exploiter des résultats d'algèbre linéaire. De nombreuses équations différentielles de la physique vérifient la propriété de linéarité.
Une équation différentielle linéaire scalaire se présente comme une relation entre une ou plusieurs fonctions inconnues et leurs dérivées, de la forme
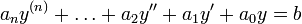
où 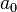 ,
, 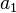 , …
, … 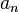 ,
, 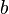 sont des fonctions numériques continues.
sont des fonctions numériques continues.
Une équation différentielle linéaire vectorielle aura le même aspect, en remplaçant les 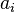 par des applications linéaires (ou souvent des matrices) fonctions de x et b par une fonction de x à valeurs vectorielles. Une telle équation sera parfois aussi appelée système différentiel linéaire.
par des applications linéaires (ou souvent des matrices) fonctions de x et b par une fonction de x à valeurs vectorielles. Une telle équation sera parfois aussi appelée système différentiel linéaire.
L'ordre de l'équation différentielle correspond au degré maximal de différentiation auquel une des fonctions inconnues y a été soumise, n dans l'exemple précédent. Il existe des méthodes générales de résolution pour les équations différentielles linéaires scalaires d'ordre 1 à coefficients variables ou d'ordre n à coefficients constants.
Généralités sur l'équation différentielle linéaire scalaire
Celle-ci s'écrit, sous sa forme la plus générale :

Équation homogène
Cette équation, appelée aussi équation sans second membre, s'écrit :

Si on dispose de n « intégrales » (i.e. : solutions) particulières linéairement indépendantes :
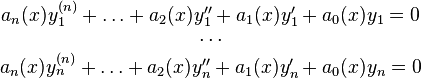
en multipliant chaque équation respectivement par les constantes  , la fonction
, la fonction
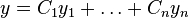
qui dépend de n constantes arbitraires satisfait l'équation : c'est l'intégrale générale de celle-ci.
Équation non homogène
Si, à cette fonction dépendant de n constantes arbitraires, est ajoutée une intégrale particulière de l'équation complète, la somme des deux satisfait l'équation complète : c'est l'intégrale générale de l'équation non homogène. Une autre méthode, celle de la variation des constantes, fournit directement (lorsqu'elle est praticable) l'intégrale générale.
Cas de l'équation à coefficients constants
L'équation s'écrit alors :
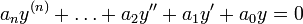
En cherchant une solution de la forme 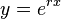 , on obtient l'équation caractéristique :
, on obtient l'équation caractéristique :

Si les 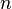 racines sont distinctes, cette équation fait apparaître les
racines sont distinctes, cette équation fait apparaître les 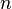 fonctions indépendantes suffisantes pour déterminer toutes les solutions de l'équation homogène. Une racine réelle correspond à une exponentielle tandis qu'une paire de racines complexes conjuguées se traduit par une exponentielle multipliée par une sinusoïde.
fonctions indépendantes suffisantes pour déterminer toutes les solutions de l'équation homogène. Une racine réelle correspond à une exponentielle tandis qu'une paire de racines complexes conjuguées se traduit par une exponentielle multipliée par une sinusoïde.
Dans le cas de l'équation complète, il ne reste plus qu'à trouver une seule solution de celle-ci. C'est particulièrement simple dans le cas important d'un second membre sinusoïdal ou lorsque celui-ci peut être décomposé en sommes de sinusoïdes (voir Analyse spectrale). Pour d'autres types de seconds membres, la transformation de Laplace fournit un certain nombre de solutions.
Équation différentielle linéaire vectorielle
Écriture générale
Soient I intervalle réel et E espace vectoriel normé. Soient n + 1 fonctions a0, a1, … an continues sur I à valeurs dans ℒ(E) et b une fonction continue sur I à valeurs dans E. L'équation

est appelée équation différentielle linéaire d'ordre n sur I.
Une solution de cette équation est une fonction y de classe Cn de I dans E telle que

Principe de superposition
L'équation homogène E0 associée à l'équation Eb ci-dessus est :

Toute combinaison linéaire de solutions, sur un sous-intervalle J de I, de l'équation homogène E0, est elle aussi solution : l'espace S0 de ces solutions est un sous-espace vectoriel de l'espace des fonctions définies sur J.
Étant donnée une solution y de Eb sur J, les autres sont les fonctions de la forme y + z avec z solution arbitraire de E0 sur J : l'espace Sb de ces solutions est un espace affine de direction S0.
Écriture matricielle
Si E est de dimension finie d, en fixant une base de E, l'équation peut s'écrire matriciellement. Soient n + 1 fonctions 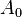 ,
, 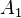 , … ,
, … , 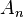 continues sur I à valeurs dans l'espace des matrices carrées Md(ℝ) et B une fonction continue sur I à valeurs dans ℝd :
continues sur I à valeurs dans l'espace des matrices carrées Md(ℝ) et B une fonction continue sur I à valeurs dans ℝd :

Forme résolue
Sur tout intervalle où  est constamment inversible, l'équation se réécrit sous forme résolue (en posant
est constamment inversible, l'équation se réécrit sous forme résolue (en posant  et
et 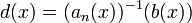 ):
):
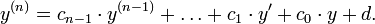
Réduction à l'ordre 1
Toute équation différentielle (linéaire) peut être vue comme une équation (linéaire) d'ordre 1, à condition de modifier l'espace vectoriel en conséquence.
On prend en effet comme nouvel espace vectoriel En, comme nouvelle fonction inconnue le vecteur
L'équation équivalente vérifiée par les composantes de Y est
qui est bien une équation différentielle d'ordre 1, et qui reste sous forme résolue si l'équation de départ l'était.
Par exemple, l'équation différentielle linéaire d'ordre deux, résolue et autonome
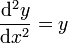
à valeurs dans ℝ se transforme en équation du premier ordre à valeurs dans ℝ2 : la fonction inconnue de la nouvelle équation différentielle est une fonction x ↦ v(x) = (y(x), z(x)) de ℝ dans ℝ2 et l'équation s'écrit :
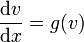
où g est l'endomorphisme de ℝ2 défini par g(y, z) = (z, y). Autrement dit :
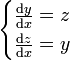
c'est-à-dire que la dérivée de la fonction y est égale à z et la dérivée de z est égale à y, ce qui signifie que la dérivée seconde de y est égale à y. La nouvelle équation est bien équivalente à l'ancienne.
Équation différentielle linéaire d'ordre 1 sous forme résolue
L'équation d'ordre 1 sert de référence pour toute la théorie, puisque les équations d'ordre supérieur peuvent s'y ramener. La forme résolue, ou explicite, permet d'avoir de bons résultats théoriques d'existence et d'unicité.
Écritures
Écriture générale
D'après ce qui précède, une équation différentielle linéaire d'ordre 1 sous forme résolue s'écrit
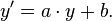
Écriture matricielle
Si E est de dimension finie d, en fixant une base de E, l'équation peut s'écrire matriciellement, avec une fonction  continue sur I à valeurs dans l'espace des matrices carrées Md(ℝ) et B une fonction continue sur I à valeurs dans ℝd. L'équation devient
continue sur I à valeurs dans l'espace des matrices carrées Md(ℝ) et B une fonction continue sur I à valeurs dans ℝd. L'équation devient
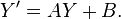
Écriture en composantes
L'écriture matricielle prend la forme d'un système

Existence et unicité des solutions
Pour identifier complètement une solution de l'équation on peut imposer des conditions initiales, c'est-à-dire la valeur y0 de y au point x0. On appelle problème de Cauchy l'ensemble constitué par l'équation différentielle Eb et la condition initiale
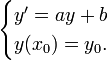
Le théorème de Cauchy-Lipschitz permet d'affirmer que ce problème de Cauchy admet une solution unique (tandis que les équations du premier ordre sous forme générale ay' + by = c – non « résolue » – ne bénéficient pas de ce théorème). De plus, par rapport aux équations différentielles générales, la particularité des équations linéaires est que les fonctions solutions sont définies sur I entier.
Autrement dit, si Sb désigne l'espace des solutions sur I de l'équation Eb, l'application valeur en x0 :
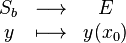
est bijective.
En particulier pour b = 0, c'est donc un isomorphisme d'espaces vectoriels et l'espace vectoriel S0 est de même dimension que E.
Si E est de dimension finie d, résoudre l'équation homogène revient donc à trouver d solutions y1, ..., yd linéairement indépendantes, qui formeront alors une base de S0. Une telle base est appelée système fondamental de solutions. L'isomorphisme de Cauchy-Lipschitz a une conséquence surprenante : si en un point x, les vecteurs y1(x), … , yd(x) sont indépendants, alors en tout autre point x', les vecteurs y1(x'), ..., yd(x') le sont également.
Pour tester si d solutions sont linéairement indépendantes, il suffit donc de vérifier si d vecteurs de E sont indépendants. On calcule donc un déterminant adapté : le wronskien.
Utilisations de l'exponentielle pour la résolution systématique
L'équation différentielle la plus simple est y' = b, qui consiste en un calcul de primitive. Sous certaines hypothèses, il est possible de se ramener à cette forme par changement de fonction. La résolution explicite des équations différentielles par des formules de quadrature, c'est-à-dire impliquant les fonctions usuelles et la primitivation, est cependant rarement possible.
Les deux cas particuliers qui suivent n'en ont que plus d'importance.
Équation différentielle linéaire scalaire d'ordre 1
On considère l'équation y' = ay + b dans le cas où E est le corps des réels ou des complexes. Soit A une primitive de la fonction a. Alors le changement de fonction
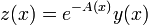
permet de ramener l'équation différentielle à un problème de calcul de primitive :
![\left[ \forall x \in I, y'(x)=a(x)y(x)+b(x)\right]\Leftrightarrow \left[\forall x \in I, \, z'(x)=e^{-A(x)} b(x)\right].](../i/m/e1429a30c7a4ef1d1c603ee03e179311.png)
Équation différentielle linéaire d'ordre 1, à coefficients constants
L'équation considérée est cette fois l'équation vectorielle y' = ay + b, mais avec l'hypothèse que a est indépendant de x, d'où l'expression coefficients constants quand on considère le système associé. Le vecteur b, lui peut être variable.
En faisant appel à la notion d'exponentielle d'endomorphisme, le changement de fonction
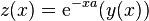
permet de ramener, là encore, l'équation différentielle à un problème de calcul de primitive
![\left[ \forall x \in I, y'(x)=a(y(x))+b(x)\right]\Leftrightarrow \left[\forall x \in I, \, z'(x)={\rm e}^{-xa} (b(x))\right].](../i/m/3427b4efd4b93d6bf7552f4a82904496.png)
(En particulier dans le cas homogène, c'est-à-dire si b = 0, la solution générale est z = constante donc y(x) = exa(y0).)
Pour résoudre effectivement une telle équation, il est donc nécessaire, outre la primitivation, de faire un calcul d'exponentielle d'endomorphisme, ce qui fait intervenir les techniques de réduction.
Cas général : résolvante
Quand on revient à l'équation vectorielle générale y' = ay + b, il est tentant de reprendre la formule de changement de fonction (A désignant une primitive de a)
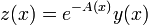
puisqu'elle fonctionne dans le cas scalaire.
Malheureusement, la formule de dérivation des exponentielles de matrices ne s'étend pas en général à ce cas-là. Le seul point sur lequel achoppe la démonstration est la non-commutation de A(x) et de A'(x), de sorte que si cette condition est réalisée pour tout x, la méthode fonctionne et on aboutit au même résultat que pour une équation scalaire. Mais cela ne procure pas de méthode générale.
Il existe toutefois une solution formelle au problème : on note R(x, x0) la solution globale, fournie par le théorème de Cauchy-Lipschitz, du problème de Cauchy à valeurs dans ℒ(E) :
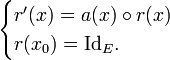
Autrement dit, la fonction de deux variables associée à l'application continue a de I dans ℒ(E) est l'application, appelée résolvante[1] :
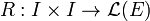
caractérisée par :

Elle fournit de ce fait la solution globale de tout problème de Cauchy à valeurs dans E de la forme

par
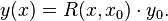
Ceci est une autre caractérisation de R, dont il résulte que
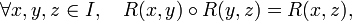
en particulier chaque R(x, y) est inversible et

On peut d'ailleurs construire R directement sans faire appel au théorème de Cauchy-Lipschitz, par une formule « explicite » bien que peu utile en pratique :
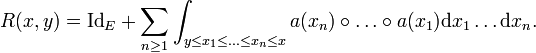
Dans le cas d'une équation à coefficients constants, la résolvante est simplement
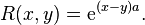
Soient K un intervalle compact de I et M(x, ξ) une fonction continue de K × K dans ℒ(E).
On définit l'opérateur  de la manière suivante :
de la manière suivante :
 Cet opérateur est linéaire. On définit maintenant la fonction à valeurs dans ℒ(E)
Cet opérateur est linéaire. On définit maintenant la fonction à valeurs dans ℒ(E)
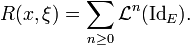 (Cette série est normalement convergente car chaque terme est borné par
(Cette série est normalement convergente car chaque terme est borné par 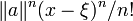 et donc cette définition de R a un sens.) On remarque que
et donc cette définition de R a un sens.) On remarque que
et on montre par ailleurs (en explicitant les 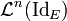 ) que pour tout entier naturel n,
) que pour tout entier naturel n,
En appliquant les formules ci-dessus, on montre que  est indépendante de y donc égale à
est indépendante de y donc égale à 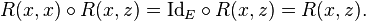
La résolvante fournit non seulement les solutions de l'équation homogène y' = ay mais permet encore de ramener l'équation générale y' = ay + b à un calcul de primitive par changement de fonction : en posant
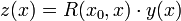
on obtient en effet

et
![\left[y(x_0)=y_0\text{ et }y'(x)=a(x)\cdot y(x)+b(x)\right]\Leftrightarrow\left[z(x_0)=y_0\text{ et }z'(x)=R(x_0,x)\cdot b(x)\right].](../i/m/ce271f49af70d2d723f4f78927b16ff6.png)
Méthode variationnelle ou des variations de constantes
On considère un système d'équations différentielles quelconque du type y' = f(x, y). On considère une solution approchée 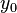 .
On définit alors
.
On définit alors 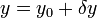 . On résout alors :
. On résout alors :
On obtient alors l'équation affine suivante:
La matrice 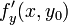 dépend de x et on utilise la méthode décrite ci-dessus. La convergence est quadratique et donc l'équation différentielle peut être résolue de manière exacte généralement en 3 à 4 itérations.
dépend de x et on utilise la méthode décrite ci-dessus. La convergence est quadratique et donc l'équation différentielle peut être résolue de manière exacte généralement en 3 à 4 itérations.
Note et référence
- ↑ Jean-Pierre Demailly, Analyse numérique et équations différentielles [détail des éditions], p. 210-211
Voir aussi
Système mécanique linéaire
- Portail de l’analyse