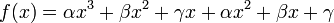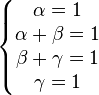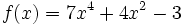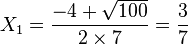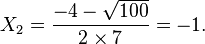Équation polynomiale
Une équation polynomiale est une équation de la forme :
où P et Q sont des polynômes.
Voici un exemple d'équation simple avec une seule inconnue :
Usuellement, le terme équation polynomiale désigne une équation avec une seule inconnue (notée ici «  ») :
») :
où les 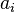 , appelés coefficients de l’équation, sont connus. Les coefficients sont le plus souvent des nombres réels ou complexes, mais ils peuvent prendre leurs valeurs dans n’importe quel anneau.
, appelés coefficients de l’équation, sont connus. Les coefficients sont le plus souvent des nombres réels ou complexes, mais ils peuvent prendre leurs valeurs dans n’importe quel anneau.
En mathématiques, l'équation polynomiale, est le sujet central de la théorie des équations. L'objectif de la théorie des équations est de trouver les racines d'un polynôme, ce qui revient à résoudre une équation polynomiale. Résoudre l’équation consiste à trouver l’ensemble des valeurs de l’inconnue  (appartenant à un certain ensemble, en général le même corps ou anneau que les coefficients), appelées solutions de l’équation, pour lesquelles l’équation polynomiale est vraie.
(appartenant à un certain ensemble, en général le même corps ou anneau que les coefficients), appelées solutions de l’équation, pour lesquelles l’équation polynomiale est vraie.
On appelle degré de l’équation la plus grande puissance de l’inconnue affectée d’un coefficient non nul. Par exemple, l’équation  d’inconnue
d’inconnue  est une équation polynomiale réelle du second degré. (Son unique solution (solution double) est
est une équation polynomiale réelle du second degré. (Son unique solution (solution double) est  .)
.)
Théorie
Polynômes
Soit l’équation d'inconnue 
dont les coefficients 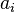 appartiennent à un corps
appartiennent à un corps  . On dit également que les solutions de (E) dans
. On dit également que les solutions de (E) dans  sont les racines sur
sont les racines sur  du polynôme
du polynôme
On montre en algèbre qu'un polynôme de degré 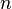 sur un corps possède au plus
sur un corps possède au plus 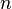 racines. L'équation (E) admet donc au plus
racines. L'équation (E) admet donc au plus 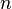 solutions.
solutions.
Si  est un surcorps de
est un surcorps de  , on peut considérer (E) comme une équation à coefficients dans
, on peut considérer (E) comme une équation à coefficients dans  ; et les solutions de (E) dans
; et les solutions de (E) dans  sont aussi solutions dans
sont aussi solutions dans  (la réciproque étant en général fausse). Il est toujours possible de trouver un surcorps de
(la réciproque étant en général fausse). Il est toujours possible de trouver un surcorps de  , appelé corps de rupture du polynôme
, appelé corps de rupture du polynôme  , dans lequel (E) admet au moins une solution.
, dans lequel (E) admet au moins une solution.
Existence de solutions pour les équations réelles et complexes
Le théorème de d'Alembert-Gauss affirme que le corps des complexes est algébriquement clos, c’est-à-dire que toute équation polynomiale à coefficients complexes et de degré au moins un admet une solution.
Il s’ensuit que toute équation polynomiale de degré un ou plus à coefficients réels admet une solution complexe. En revanche, une équation comme 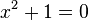 n’a pas de solution dans
n’a pas de solution dans 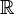 (ses solutions sont les complexes
(ses solutions sont les complexes 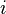 et
et  ).
).
Autant l'intuition des solutions réelles d'équations réelles 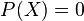 est immédiate (ce sont les points de la courbe Y=P(X) qui rencontrent l'axe (ox)), autant l'existence de ces solutions complexes d'équations réelles peut paraître étonnante et leur localisation indéterminable intuitivement.
est immédiate (ce sont les points de la courbe Y=P(X) qui rencontrent l'axe (ox)), autant l'existence de ces solutions complexes d'équations réelles peut paraître étonnante et leur localisation indéterminable intuitivement.
Toutefois, une équation polynomiale réelle de degré impair admet nécessairement une solution réelle. En effet, la fonction polynôme associée est continue, et elle tend vers 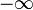 au voisinage de
au voisinage de 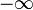 et vers
et vers 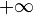 au voisinage de
au voisinage de 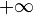 . D’après le théorème des valeurs intermédiaires, elle prend donc la valeur zéro en un certain réel, qui est ainsi solution de l’équation.
. D’après le théorème des valeurs intermédiaires, elle prend donc la valeur zéro en un certain réel, qui est ainsi solution de l’équation.
Lien avec la théorie de Galois
On dispose de formules donnant les solutions des équations polynomiales réelles ou complexes de degré inférieur ou égal à quatre en fonction de leurs coefficients. Abel a montré qu’il n’est pas possible de trouver de telles formules générales (n’utilisant que les quatre opérations usuelles et les racines) pour les équations de degré cinq ou plus. La théorie de Galois donne un critère permettant de déterminer, étant donnée une équation polynomiale, si sa solution s’exprime par radicaux.
Résolution explicite des équations numériques
Démarche
La résolution explicite d’une équation réelle ou complexe du premier degré est immédiate. Résoudre une équation de degré supérieur 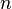 revient à factoriser le polynôme associé, c’est-à-dire à réécrire (E) sous la forme
revient à factoriser le polynôme associé, c’est-à-dire à réécrire (E) sous la forme
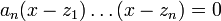 ,
,
où apparaissent naturellement les solutions  . On cherche donc à exprimer les
. On cherche donc à exprimer les 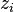 en fonction des
en fonction des 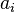 .
.
Cette démarche s’applique plus généralement si coefficients et solutions prennent leurs valeurs dans un anneau intègre.
Second degré
Pour résoudre une équation du second degré du type  on calcule son discriminant Δ défini par
on calcule son discriminant Δ défini par 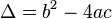 .
.
Si 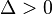 , alors l’équation a deux racines réelles distinctes
, alors l’équation a deux racines réelles distinctes 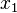 et
et 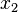 , telles que :
, telles que :

 .
.
Si  , l’équation a alors une racine réelle double
, l’équation a alors une racine réelle double 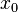 , telle que :
, telle que :
 .
.
Si  , il n’existe aucune racine réelle au trinôme. Cependant il possède deux racines complexes conjuguées
, il n’existe aucune racine réelle au trinôme. Cependant il possède deux racines complexes conjuguées 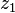 et
et 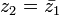 . Si
. Si  , on peut écrire :
, on peut écrire :
Équations se ramenant au second degré
Certaines équations de degré trois ou quatre se ramènent facilement à des équations du second degré. Leur résolution nécessite de connaître la formule de résolution des équations du second degré et les nombres complexes.
Premier exemple : racine(s) évidente(s)
Lorsqu’une équation de degré 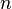 admet une solution évidente, on peut factoriser le polynôme associé en un facteur du premier degré et un polynôme de degré
admet une solution évidente, on peut factoriser le polynôme associé en un facteur du premier degré et un polynôme de degré 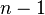 . La résolution de l’équation se ramène donc à celle d’une équation de degré
. La résolution de l’équation se ramène donc à celle d’une équation de degré 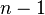 .
.
On se propose d’étudier pour quelles valeurs de  la fonction réelle
la fonction réelle 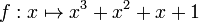 , polynomiale de degré 3, s’annule.
, polynomiale de degré 3, s’annule.
On remarque tout d’abord que 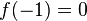 . Donc -1 est une racine du polynôme.
. Donc -1 est une racine du polynôme.
On cherche alors 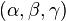 tels que
tels que
-
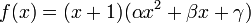 .
.
On a :
Or deux polynômes sont égaux s’ils sont de même degré et si leurs coefficients respectifs sont égaux deux à deux. Donc :
et
Ainsi,
 ,
,
et résoudre  revient à résoudre
revient à résoudre 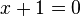 , puisque
, puisque  . L’unique solution réelle de l’équation est
. L’unique solution réelle de l’équation est  .
.
Deuxième exemple : équations bicarrées
On se propose de rechercher les racines du polynôme bicarré
(est dit bicarré tout polynôme de la forme
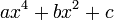 ).
Pour cela, nous allons réaliser un changement d’inconnue.
).
Pour cela, nous allons réaliser un changement d’inconnue.
Posons 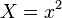 , on a alors
, on a alors  . L’équation du second degré obtenue a pour discriminant
. L’équation du second degré obtenue a pour discriminant  . Ses solutions sont donc
. Ses solutions sont donc
Ces solutions sont exactement les carrés des solutions de l’équation de départ
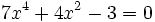 .
.
L’ensemble des racines de 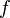 est donc
est donc
 .
.
Troisième exemple, où x ↦ ax + b√x + c
L’objectif est ici d’étudier les solutions de l’équation  , avec
, avec  . Cela illustre que certaines équations non polynomiales se ramènent, elles aussi, à des équations polynomiales du second degré.
. Cela illustre que certaines équations non polynomiales se ramènent, elles aussi, à des équations polynomiales du second degré.
On pose  ; on peut donc écrire
; on peut donc écrire 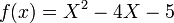 . On résout alors l’équation f(x) = 0 d’inconnue
. On résout alors l’équation f(x) = 0 d’inconnue 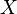 :
: 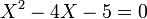 équivaut à
équivaut à  . Les solutions sont donc
. Les solutions sont donc 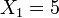 et
et  . La solution
. La solution  doit être rejetée car le changement de variable
doit être rejetée car le changement de variable  impose
impose 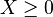 .
.
La seule solution possible de  est donc :
est donc : 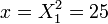
Troisième degré
Pour résoudre une équation du troisième degré, on peut tenter de ramener l’équation à une multiplication de deux polynômes plus simples en trouvant une racine évidente (voir ci-dessus).
Mais il existe une méthode générale permettant de résoudre n'importe quelle
équation du type  . Leonhard Euler a résolu ces équations en commençant par rendre nul le terme de degré inférieur à celui du terme dominant. En effet, en posant
. Leonhard Euler a résolu ces équations en commençant par rendre nul le terme de degré inférieur à celui du terme dominant. En effet, en posant 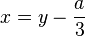 , ces équations peuvent être ramenées à la forme :
, ces équations peuvent être ramenées à la forme :
 .
.
Or Jérôme Cardan a résolu ce type équations de degré trois et a exprimé les racines sous la forme de radicaux. C'est ce qu'on appelle la Méthode de Cardan (Résolution des équations de degré trois).
Quatrième degré
Pour résoudre une équation du quatrième degré, on peut tenter de ramener l’équation à une multiplication d’au moins deux polynômes plus simples (voir ci-dessus).
Pour un exposé détaillé de certaines méthodes de résolution voir :
- Méthode de Tschirnhaus (Méthode générale qui peut ne pas aboutir).
- Méthode de Bézout (Méthode générale qui peut ne pas aboutir).
- Méthode de Ferrari (Résolution des équations de degré 4).
- Méthode d'Euler (Résolution des équations de degré 4).
- Équation quartique (Racines des équations de degré 4, méthode de Lagrange)
- Méthode de Descartes (Résolution des équations de degré 2 et 4).
Équations de degré supérieur
Évariste Galois et Niels Henrik Abel ont démontré, indépendamment l’un de l’autre, que d’une manière générale une équation polynomiale de degré 5 ou plus n’est pas résoluble par radicaux (voir paragraphe Théorie ci-dessus). Des exemples d'équations non résolubles par radicaux sont donnés dans les deux articles détaillés. Certaines équations particulières le sont, comme celles associées aux polynômes cyclotomiques d'indice 5 ou 17.
Charles Hermite a en revanche démontré que les équations polynomiales de degré 5 sont résolubles à l’aide des fonctions elliptiques.
Voir en particulier : Méthode d'Hermite.
Voir aussi
Articles connexes
- Équation
- Équation du second degré | Équation cubique | Équation quartique | Équation quintique| Équation sextique (en) | Équation septique (en)
- Histoire des polynômes
- Polynôme formel | Fonction polynôme
- Nombre constructible | Nombre complexe
- Fonction elliptique
- Théorie de Galois
- Relations entre coefficients et racines
- Racine d'un polynôme
Lien externe
« Recherche instantanée des racines d'un polynôme de degré quelconque » sur le site personnel de Jean-Christophe Michel
« Programme en JavaScript pour calculer les racines d'un polynôme de degré quelconque par la méthode de Bairstow (en) » sur le site personnel d'Eric Leydet
- Portail de l’algèbre
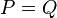
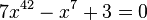
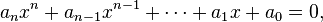

![P = a_n X^n + a_{n - 1} X^{n - 1} + \cdots + a_1 X + a_0 \quad \in \mathbb K[X],](../i/m/346c4ab06057f380b4136b5c6f239500.png)