Topologie algébrique

Cet article est une ébauche concernant la topologie et l'algèbre. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

La topologie algébrique, anciennement appelée topologie combinatoire, est une branche des mathématiques appliquant les outils de l'algèbre dans l'étude des espaces topologiques. Plus exactement, elle cherche à associer de manière naturelle des invariants algébriques aux structures topologiques associées. La naturalité signifie que ces invariants vérifient des propriétés de fonctorialité au sens de la théorie des catégories.

Invariants algébriques

L'idée fondamentale est de pouvoir associer à tout espace topologique des objets algébriques (nombre, groupe, espace vectoriel…), de sorte qu'à deux espaces homéomorphes soient associées deux structures isomorphes. De tels objets sont appelés des invariants algébriques. En termes savants, il s'agit d'étudier des foncteurs depuis la catégorie des espaces topologiques sur une catégorie algébrique, comme les catégories de groupes, algèbres, groupoïdes, etc. Des résultats de topologie passent alors par la démonstration plus abordable de propriétés algébriques.

Parmi les invariants notables, citons :

• Le groupe fondamental d'un espace topologique X en un point x : l'ensemble des classes d'homotopie des lacets de X de base x, la loi de composition interne étant la concaténation des lacets ;
• Les groupes d'homotopie supérieure d'un espace topologique X en un point x ;
• Les groupes d'homologie ou de cohomologie d'un espace topologique X ;
• Les classes caractéristiques d'un fibré vectoriel réel, complexe, euclidien ou hermitien.

Applications de la topologie algébrique

• Le théorème du point fixe de Brouwer : toute application continue du disque unité de 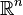dans lui-même admet un point fixe.
• Le théorème de la boule chevelue : tout champ continu de vecteurs tangents à une sphère de dimension paire s'annule en au moins un point, en conséquence un tokamak ne peut avoir une géométrie sphérique.
• Le théorème de Borsuk-Ulam : pour toute application continue de la sphère Sⁿ dans 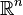il existe un couple de points antipodaux qui prennent la même valeur par cette application. Par exemple, à tout instant, il existe deux points à la surface de la Terre diamétralement opposés ayant même température et même pression.

Topologues algébriques notables

Importants théorèmes en topologie algébrique

Référence

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Algebraic topology » (voir la liste des auteurs).

• Daniel Tanré, Yves Félix, Topologie algébrique, Dunod, 2010

Article connexe

CW-complexe

• Portail des mathématiques