Taux de croissance annuel moyen
|
|
Cet article est une ébauche concernant les mathématiques. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
|
Le taux de croissance annuel moyen (TCAM) permet de calculer un taux d'évolution moyen sur une durée de n périodes. D'autres dénominations existent, telles TAMA (Taux Annuel Moyen d'Accroissement), TAAM (Taux d'Accroissement Annuel Moyen), ou TAMV (Taux Annuel Moyen de Variation).
Formule
Le taux de croissance annuel moyen, exprimé en pourcentage, sur 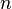 périodes (années, mois, semaines, etc.) est donné par la formule :
périodes (années, mois, semaines, etc.) est donné par la formule :
Exemple : si entre 1997 et 2008, le montant des crédits distribués est passé de 48003,1 à 249012,3 millions de francs congolais, le taux de croissance annuel moyen sur ces onze années est donné par la formule
Soit un taux d'accroissement annuel moyen de 16,14 %
Intérêt
L'intérêt du TCAM est de fournir une indication sur le taux de croissance moyen sur une période donnée. Et la comparaison de deux TCAM permet, par suite, de comparer les fluctuations du phénomène observé relativement à ces deux périodes. Par exemple, en économie, une application du TCAM est de comparer la croissance pendant les Trente Glorieuses (1945-1975) avec la croissance de la période suivante (1975 à aujourd'hui).
Cet outil de calcul est en outre employé en démographie pour décrire le taux d’accroissement de la population entre deux recensements (solde démographique relatif).
Limites
Le TCAM donne une moyenne des évolutions annuelles mais ne tient pas compte des variations internes de la période étudiée. En effet seules les valeurs initiales et finales rentrent dans son calcul.
- Portail des probabilités et de la statistique

![TCAM = \left(\sqrt[n]{\cfrac{\text{valeur finale}}{\text{valeur initiale}}}-1\right) \times 100](../i/m/34ad67e451474c16fd129f19452ef4bf.png)
![\left(\sqrt[11]{\frac{249012,3}{48003,1}} - 1\right)\times 100 \approx 16,14](../i/m/7db149939ff897f6d96097740e92827a.png)