Sémantique des langages de programmation

Cet article ne cite pas suffisamment ses sources (novembre 2012). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références » (modifier l'article, comment ajouter mes sources ?).

En informatique théorique, la sémantique formelle (des langages de programmation) est l’étude de la signification des programmes informatiques vus en tant qu’objets mathématiques.

Lien avec la linguistique

Comme en linguistique, ici la sémantique désigne le lien entre un signifiant, le programme, et un signifié, objet mathématique qui dépendra des propriétés que l’on souhaite connaître du programme.

On appellera aussi sémantique le lien entre le langage signifiant (le langage de programmation) et le langage signifié (logique de Hoare, automates, ou autre).

Sémantiques usuelles d’un langage de programmation

Les sémantiques les plus couramment utilisées pour donner du sens à un langage de programmation sont la sémantique opérationnelle, la sémantique dénotationnelle et la sémantique axiomatique.

La sémantique opérationnelle

En sémantique opérationnelle^[1], la signification d’un programme est la suite des états de la machine qui exécute le programme. Autrement dit un programme est considéré comme la description d’un système de transition d'états. Dans cette sémantique, les programmes :

a=1; b=0

et

a=1;
b=0

sont équivalents (ont la même signification), mais le programme :

b=0; a=1

ne leur est pas équivalent (même si à la fin le résultat est le même, les actions n’ont pas lieu dans le même ordre).

On peut abstraire cette sémantique en n’observant qu’une partie de la mémoire de la machine, ou par exemple en n’observant que les sorties à l’écran (la trace du programme).

La sémantique dénotationnelle

Initiée par Christopher Strachey et Dana Scott, la sémantique dénotationnelle^[2] est une approche dans laquelle une fonction mathématique appelée dénotation est associée à chaque programme, et représente en quelque sorte son effet, sa signification. Cette fonction prend par exemple pour argument l’état de la mémoire avant exécution, et a pour résultat l’état après exécution.

Dans cette sémantique, tous les exemples donnés ci-dessus pour la sémantique opérationnelle sont équivalents, mais le programme :

a=1;
b=1;

ne leur est pas équivalent.

Il existe plusieurs variantes de la sémantique dénotationnelle, dont l’une des plus célèbres est la sémantique dénotationnelle par continuation qui, au lieu d’associer à un programme une fonction qui transforme la mémoire, lui associe une fonction qui transforme la continuation (le futur) de la machine après exécution du programme en la continuation avant exécution du programme.

Un des aspects importants de la sémantique dénotationnelle est la propriété de compositionnalité : la dénotation d'un programme est obtenue par combinaison des dénotations de ses constituants.

La sémantique axiomatique

En sémantique axiomatique^[3], le programme n’est plus qu’un transformateur de propriétés logiques sur l’état de la mémoire : si on a p vrai avant exécution, alors on a q vrai après. On ne s’intéresse plus à l’état précis de la mémoire tant que l’on sait dire si la propriété tient.

Si la propriété qui nous intéresse, c’est de savoir si a et b sont positifs après exécution du programme, alors tous les exemples précédents sont équivalents au sens où quel que soit l’état de la machine avant exécution du programme, la propriété en sortie tient. Ce que l’on note en logique de Hoare :

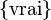a=1; b=0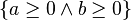

Rapport entre les différentes sémantiques

Ces trois sémantiques, comme le suggèrent les exemples, ne sont pas complètement indépendantes les unes des autres, en effet :

• deux programmes syntaxiquement équivalents le sont opérationnellement ;
• deux programmes opérationnellement équivalents le sont dénotationnellement ;
• et deux programmes dénotationnellement équivalents le sont axiomatiquement.

Mais les réciproques sont fausses.

Ainsi on peut hiérarchiser les sémantiques en disant qu’une sémantique est l’abstraction d’une autre si et seulement si deux programmes équivalents dans la dernière le sont aussi dans la première. Ces relations ont été formalisées par la théorie de l’interprétation abstraite.

On peut compléter cette hiérarchie (ordre partiel) sur les équivalences sémantiques, en plaçant au sommet l’identité (deux programmes sont identiques si et seulement s'ils sont la même suite de caractères), et tout en bas, l’abstraction la plus grossière que l’on appelle le chaos, où tout programme est équivalent à tout autre programme.

Références

• Portail de l'informatique théorique