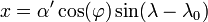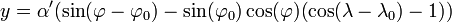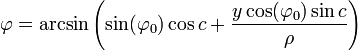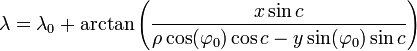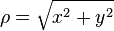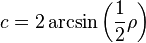Projection azimutale équivalente de Lambert

Cet article est une ébauche concernant les mathématiques et l'information géographique.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

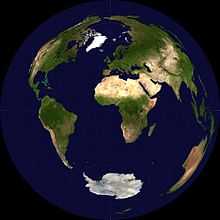
La projection azimutale équivalente de Lambert de la Terre. Son centre est 0° N 0° E dont l'antipode 0° N 180° E se situe près de Kiribati dans l'Océan Pacifique. Cet antipode ainsi projeté forme la circonférence du disque.

La projection azimutale équivalente de Lambert est une manière de projeter une sphère sur un plan, et en particulier, une façon de représenter entièrement la surface de la Terre sous la forme d'un disque. C'est donc une projection cartographique azimutale conçue (parmi d'autres) en 1772^[1] par le mathématicien alsacien Johann Heinrich Lambert.

Description

Schématisation en coupe de la projection de la sphère sur le plan.

Cette projection de Lambert "projette directement" sur un plan (projection azimutale) et conserve localement les surfaces (projection équivalente) ; mais ne conserve pas les angles (projection non conforme). Elle est assez proche (à petite échelle) de la projection perspective et plus particulièrement de la projection stéréographique où la représentation des parallèles divergent également.

Définition mathématique

Les formules^[2] de cette projection cartographique ont la même forme générale que celles de la projection perspective :

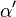$x=\alpha' \cos(\varphi)\sin(\lambda-\lambda_0)$

$y=\alpha' (\sin(\varphi-\varphi_0)-\sin(\varphi_0)\cos(\varphi)(\cos(\lambda-\lambda_0)-1))$

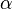mais $\alpha'$ est plus complexe que $\alpha$ :

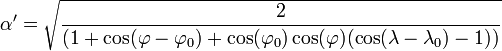
$\alpha'=\sqrt{{2 \over (1+\cos(\varphi-\varphi_0)+\cos(\varphi_0)\cos(\varphi)(\cos(\lambda-\lambda_0)-1))}}$

La transformation inverse est donnée par les formules :

$\varphi = \arcsin \left({\sin(\varphi_0) \cos c + { y\cos(\varphi_0) \sin c \over \rho}}\right)$

$\lambda = \lambda_0 + \arctan\left({x\sin c \over \rho\cos(\varphi_0) \cos c - y\sin(\varphi_0)\sin c}\right)$

où

$\rho = \sqrt{x^2 + y^2}$

$c = 2 \arcsin \left({1 \over 2}\rho \right)$

Notes et références

↑ (en) Karen Mulcahy, « Lambert Azimuthal Equal Area », City University of New York (consulté le 10 novembre 2008)
↑ Source : Lambert Azimuthal Equal-Area Projection.

Voir aussi

Projection cartographique

Les trois autres projections azimutales principales :

Projection stéréographique
Projection gnomonique
Projection orthographique

Portail de la géodésie et de la géophysique
Portail de la géographie
Portail de la géométrie
Portail de l’information géographique

This article is issued from Wikipédia - version of the Friday, May 15, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Projection azimutale équivalente de Lambert

Description

Définition mathématique

Notes et références

Voir aussi

Medical Encyclopedia