Prévision numérique du temps

 Pour l’article homonyme, voir Prévision. 

Exemple de sortie de carte avec contours en noir des isohypses de la hauteur du géopotentiel de la pression de 500 hPa par un modèle de prévision numérique

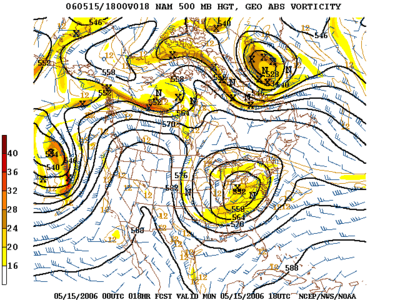
La prévision numérique du temps (PNT) est une application de la météorologie et de l'informatique. Elle repose sur le choix d'équations mathématiques offrant une proche approximation du comportement de l'atmosphère réelle. Ces équations sont ensuite résolues, à l'aide d'un ordinateur, pour obtenir une simulation accélérée des états futurs de l'atmosphère. Le logiciel mettant en œuvre cette simulation est appelé un modèle de prévision numérique du temps.

Utilisations

• En météorologie opérationnelle, la PNT est utilisée pour faire des prévisions dont les résultats numériques bruts subiront diverses formes de post-traitements pour les rendre utilisables. Les résultats seront traités par d'autres logiciels ou interprétés par des météorologues pour satisfaire les besoins spécifiques des utilisateurs. Cela inclut la prévision météorologique publique et des applications dans un grand nombre de domaines d'activité, tels que les transports, l'agriculture, la mitigation (atténuation) des désastres, etc.

• Les résultats de prévisions numériques servent à piloter d'autres modèles spécialisés. Il peut s'agir par exemple de modèles de dispersion et de trajectoire de polluants atmosphériques, ou de modèles de chimie atmosphérique pour la prévision de la qualité de l'air (prévision de smog, notamment).

• La PNT peut servir, en recherche, à faire des études de cas en « vase clos », pour étudier une facette ou un comportement particulier de l'atmosphère ou tester des améliorations au modèle en fonction de cas théoriques ou pratiques dont on connaît d'avance les résultats. Le modèle de PNT devient ainsi un laboratoire virtuel pour l'étude de l'atmosphère et l'amélioration des prévisions.

• Les modèles de PNT peuvent aussi servir à la prévision climatique. On s'intéresse alors au comportement moyen de la prévision sur une longue période et non plus à prévoir des événements spécifiques. En changeant certains aspects de la prévision, comme le taux d'augmentation du gaz carbonique, les modèles de prévision climatique aident à formuler des scénarios quant aux conséquences du changement climatique. L'étude de ces scénarios contribue à guider le public et les décideurs face au réchauffement climatique.

Historique

En 1904, Vilhelm Bjerknes fut le premier à proposer que la prévision du comportement de l'atmosphère pourrait être traitée comme un problème de physique mathématique posé en fonction des conditions initiales. La discipline de la prévision numérique du temps fut fondée en 1922 par la publication du livre Weather Prediction by Numerical Process, du mathématicien britannique Lewis Fry Richardson. Deux décennies avant l'invention de l'ordinateur, Richardson envisagea de faire résoudre numériquement, par une armée de calculateurs humains, les équations développées par Bjerknes. La vision pionnière de Richardson commença à porter ses fruits en 1950, alors que Charney, Fjortoft et von Neumann réussirent la première prévision numérique du temps par ordinateur. Les premiers programmes de prévisions numériques opérationnelles furent instaurés au début des années 1960.

En présence d'une forte demande pour des prévisions météorologiques dans de nombreux domaines d'activité, la discipline n'a cessé depuis lors de se développer, soutenue par l'augmentation de la puissance de calcul et nourrie de progrès théoriques énormes en méthodes numériques et en météorologie.

Approche mathématique

Les modèles de prévision numérique du temps utilisent les lois de la dynamique des fluides et de la chimie de l'atmosphère pour assimiler les données météorologiques disponibles sur une grille de calcul et projeter leur évolution dans le temps

En physique et en génie, l'approche classique pour obtenir des équations possédant une valeur prédictive consiste à résoudre une ou plusieurs équations différentielles contenant la variable temporelle. Dans les cas les plus commodes, la solution exprime les variables à prévoir en fonction du temps et des conditions initiales (les valeurs des variables au moment choisi pour le début de la prévision). Il suffit alors de nourrir cette équation avec les valeurs numériques requises pour obtenir une solution dite exacte. L'oscillateur harmonique est un exemple d'un problème classique qui se prête bien à cette approche.

Le problème du comportement futur de l'atmosphère est beaucoup plus complexe et n'a de solution exacte que dans quelques sous-ensembles théoriques très restreints. Pour résoudre les équations de la PNT dans le monde réel, il faut utiliser les méthodes de l'analyse numérique. Ces méthodes permettent de reformuler les équations du comportement atmosphérique de manière à pouvoir les résoudre par de nombreuses itérations de calculs numériques bruts. On fait ainsi progresser, dans le modèle, l'état de l'atmosphère à partir d'un point de départ jusqu'à l'intervalle de prévision voulu.

L'inconvénient de ces méthodes numériques est qu'elles exigent de faire une approximation de la continuité du temps et de l'espace sur une grille de calcul; la simulation devient ainsi discontinue dans le temps et l'espace. Les résultats, visualisés sur leur grille de calcul, ont une apparence « pixelisée », semblable à une image numérique. De même, le temps n'est plus une variable continue, les calculs sautant d'une étape temporelle à la suivante.

Exemple typique: l'une des configurations opérationnelles du modèle GEM d'Environnement Canada (en date de 2005) morcelle l'espace de l'Amérique du Nord et les eaux adjacentes en tuiles de 15 km de côté. La taille de ces tuiles définit la résolution horizontale, ou la maille du modèle. De plus, le modèle représente la dimension verticale de l'atmosphère en la divisant en 58 niveaux. Et finalement, chaque ronde de calculs du modèle fait avancer la prévision de 450 secondes. L'intervalle de temps-modèle entre les rondes de calculs est appelé le pas de temps.

En règle générale, il est souhaitable de faire en sorte que le modèle ait la maille la plus fine possible. Cela augmente le réalisme du modèle et minimise l'accumulation de petites erreurs de calculs inhérentes aux méthodes de l'analyse numérique. Par ailleurs, pour une résolution donnée, il existe un pas de temps maximum qu'il ne faut pas dépasser afin de préserver la stabilité et le réalisme des résultats numériques.

Paramétrisation sous-maille

Pour obtenir une bonne prévision, il faut aussi tenir compte de phénomènes qui sont plus petits que la résolution du modèle (phénomènes dits sous-maille). Par exemple, un orage est considérablement plus petit que la maille de la plupart des modèles à grande échelle ; pris isolément on pourrait se permettre de le négliger dans le cadre d'une prévision à l'échelle d'un pays ou d'un continent. Mais une zone orageuse, comprenant de nombreux orages dans un domaine géographique étendu, aura un impact important sur le déroulement du cas qui fait l'objet de la prévision, de par la production d'une quantité appréciable de pluie et de son effet dans le bilan énergétique de l'atmosphère. Plus fondamentalement encore : laissé à lui-même, le modèle pourrait créer des orages dont la taille horizontale égalerait la maille du modèle, ce qui est complètement irréaliste et fausserait de manière brutale l'évolution de la prévision. On doit donc donner aux orages une existence implicite au sein du modèle afin de dissiper l'énergie convective en respectant les considérations d'échelle.

La représentation de l'influence moyenne à grande échelle des phénomènes de la petite échelle est appelée paramétrisation. Les phénomènes sous-maille les plus communément paramétrisés par les concepteurs des modèles sont :

• La convection verticale (dont font partie les orages)
• La physique des nuages (condensation, collection et collision des gouttes, effet Bergeron, changements de phase, etc.)
• Les effets radiatifs atmosphériques (rayonnement de la chaleur)
• L'interface surface-air :
  • Échanges de chaleur et d'humidité entre la surface et l'atmosphère
  • Frottement et turbulence près du sol
• L'effet des montagnes et des irrégularités du terrain :
  • Effet de blocage du vent
  • Ondes atmosphériques en aval des montagnes

Le paramétrage des phénomènes physiques ne compense pas complètement les limitations imposées par un espacement trop grand de la maille des modèles. Le choix et l'ajustement des schémas de paramétrisation a un impact important sur la qualité des prévisions.

Couverture géographique et intervalle de prévision

Pour répondre à des besoins immédiats en matière de prévision du temps, il faut atteindre un compromis acceptable pour maximiser la résolution spatio-temporelle du modèle tout en tenant compte:

• de l'intervalle de prévision voulu (48 heures, dix jours, trois mois ?)
• de la taille du domaine géographique de prévision (pays, continent, monde ?)
• des échéances de production et des exigences de fiabilité
• des ressources informatiques, économiques et humaines disponibles

Pour les prévisions à court terme, l'état de l'atmosphère dans des régions éloignées importe peu. Une perturbation actuellement sur l'Amérique mettra quelques jours à se propager et à faire sentir son influence sur l'Europe. On peut alors choisir de concentrer une zone de maille fine du modèle sur la région d'intérêt, négligeant ainsi les phénomènes lointains. On parle alors d'un modèle régional.

Pour des prévisions à plus long terme, disons au-delà de deux ou trois jours, il devient nécessaire d'augmenter la couverture du modèle à un hémisphère complet ou encore à tout le globe, afin de bien traiter les phénomènes encore lointains qui se propageront vers la zone d'intérêt. Pour la même raison, la maille du modèle est répartie de manière uniforme sur le globe. Les modèles hémisphériques étant tombés en désuétude, ce type de prévision échoit au modèle mondial.

Considérations informatiques

En théorie, en augmentant la résolution du modèle, on en augmenterait le réalisme et on réduirait le besoin de recourir à la paramétrisation; toutefois, cela ne peut se faire qu'à un coût informatique et économique considérable, surtout s'il faut obtenir la prévision à l'intérieur d'échéances serrées.

Exemple : si on double la résolution spatiale d'un modèle donné, le nombre de points dans la grille de calcul augmente d'un facteur 8 ; et si l'on réduit par la même occasion de moitié le pas de temps (doublant ainsi la résolution temporelle), la prévision devient donc 16 fois plus coûteuse informatiquement que la version précédente du modèle. Pour faire face à ce problème, il ne suffit pas de multiplier la puissance brute de calcul : le volume de données à transférer lors des calculs et lors de la mise en stockage des résultats augmente lui aussi par le même facteur. On peut ainsi voir que les opérations d'entrée-sortie, qui constituent un goulot d'étranglement dans tout type d'ordinateur, peuvent devenir un obstacle sérieux à l'augmentation de la résolution des modèles de PNT.

Prévisibilité

La prévisibilité est la limite de la possibilité de prévoir numériquement les états futurs de l'atmosphère en utilisant un réseau d'observation donné. Elle est définie habituellement par l'échéance en deçà de laquelle il faut s'attendre que l'erreur quadratique moyenne d'un champ prévu soit inférieure à la différence quadratique moyenne entre deux états atmosphériques observés choisis au hasard^[1]. En pratique, cela se traduit par la stabilité de la solution de la prévision à un temps X avec les donnés disponibles, connaissant leurs erreurs intrinsèques et leur distribution spatiale, si une légère variation des valeurs est introduite dans ces données. Le moment où la solution commence à diverger entre les calculs provenant des différentes perturbations devient la limite de prévisibilité du système météorologique.

Sources d'erreur

• Données initiales : erreurs de mesure et d'analyse
• Couverture de données : typiquement plus pauvre sur les océans et dans les zones peu peuplées ou économiquement défavorisées
• Erreurs inhérentes aux méthodes de calcul numérique adoptées
• Erreur causée par la maille du modèle : plus la maille est grossière, moins le modèle est apte à bien représenter les phénomènes de moyenne et petite échelle
• Erreurs de paramétrisation

Importance des données initiales et de l'analyse

Même un modèle parfait (exempt des trois dernières sources d'erreurs) ne pourrait produire une prévision parfaite, car les erreurs dans les conditions initiales iront en s'amplifiant lors de la prévision et celle-ci divergera de la réalité^[2].

Il est donc nécessaire de connaître avec le plus de précision possible l'état initial de l'atmosphère. Déterminer cet état, appelé analyse est en soi un grand défi scientifique qui exige des ressources mathématiques et informatiques comparables à celles dévouées à la prévision elle-même. Les sources de données sont disparates, traditionnellement constituées des observations de surface, s'y ajoutent les données de radiosondage, de profileurs de vent et les mesures effectuées par les avions commerciaux. Actuellement les mesures satellites représentent la source de données la plus importante, et depuis peu, les réflectivités et vitesses radiales radar sont également prises en compte dans certains modèles de mésoéchelle.

Cependant l'utilisation des seules données d'observation n'est pas suffisante. D'une part le nombre de variables d'un modèle numérique est supérieur au nombre d'observations, d'autre part une analyse effectuée directement par interpolation des observations aboutirait à un comportement instable du modèle. C'est une des raisons de l'échec des premières tentatives de modélisation du comportement de l'atmosphère par Richardson^[3].

Pour construire l'analyse, on a donc recours à une ébauche, c'est-à-dire la prévision effectuée précédemment, généralement 6 ou 12 heures auparavant. Cette ébauche est alors corrigée pour s'ajuster au plus près des observations, généralement en tenant compte des erreurs d'observation^[2]. L'approche la plus communément utilisée actuellement utilise les méthodes du calcul des variations pour déterminer le meilleur compromis entre l'ébauche et les observations, compte tenu de leurs erreurs respectives. Cette approche est désignée par le terme « 3D-Var » lorsqu'elle ne tient compte que de l'état du modèle et des observations valides à l'heure d'analyse, et « 4D-Var » lorsqu'elle tient également compte de l'évolution de ces derniers sur une fenêtre temporelle.

Toutes ces méthodes constituent l'assimilation de données, devenu un domaine de recherche à part entière.

Prévisions d'ensembles

Dans les premières décennies d'existence de la prévision numérique du temps, on devait se satisfaire de faire tourner un modèle à la plus haute résolution permise par les contraintes informatiques, et à adopter cette prévision telle quelle. Cette approche suppose implicitement que si les conditions initiales étaient connues parfaitement, et que le modèle lui-même était parfait, la prévision qui s'ensuivrait simulerait parfaitement le comportement futur de l'atmosphère. On qualifie cette approche de déterministe.

En pratique, ni les observations, ni l'analyse, ni le modèle ne sont parfaits. Par ailleurs, la dynamique atmosphérique est très sensible, dans certaines conditions, à la moindre fluctuation. Une nouvelle approche probabiliste a donc été développée, celle de la prévision d'ensemble. La prévision d'ensemble sacrifie la résolution afin de pouvoir consacrer des ressources informatiques à faire tourner simultanément de nombreux exemplaires de modèles sur le même cas de prévision. Dans chaque cas, l'analyse est délibérément rendue légèrement différente des autres membres de l'ensemble, à l'intérieur des incertitudes intrinsèques de mesure ou d'analyse. Les scénarios plus ou moins divergents des prévisions offertes par les membres de l'ensemble permettent de quantifier la prévisibilité de l'atmosphère et d'offrir une marge d'erreur statistique sur la prévision. Le défi dans la conception d'un tel système est de faire en sorte que les fluctuations qu'on y observe constituent un signal représentatif de l'incertitude naturelle de la dynamique atmosphérique.

Certains systèmes de prévision d'ensemble (SPE) font aussi varier les méthodes de paramétrage des modèles membres de l'ensemble afin qu'une partie des fluctuations des prévisions représente les incertitudes de modélisation. Dans la même veine, il y a un intérêt marqué, dans la communauté de recherche sur les prévisions d'ensembles, envers les ensembles multi-modèles (c’est-à-dire combinant des modèles de différentes conceptions) et l'agrégation de SPE de différents pays en un super-ensemble. Il existe en ce moment (2006) deux efforts concrets en ce sens, soit le Système nord-américain de prévision d'ensemble (Canada, États-Unis, Mexique) et le "THORPEX Interactive Grand Global Ensemble", ou TIGGE (sous la coordination de l'Organisation météorologique mondiale).

Approche opérationnelle

La mise en œuvre de la PNT aux fins de la prévision opérationnelle du temps (par opposition à la recherche pure) suppose invariablement les étapes suivantes, dont la mise en œuvre peut différer quelque peu selon le lieu et les circonstances d'application :

• Acquisition des données d'observations météorologiques (de stations terrestres, navires, aéronefs, radio-sondes, données satellitaires de mesures à distance, etc.)
• Décodage et contrôle de la qualité des observations
• Analyse (élaboration d'une représentation numérique de l'état de l'atmosphère au début de la prévision)
• Lancement du modèle de prévision avec l'analyse comme point de départ
• Post-traitement des sorties du modèle : production d'images, de bulletins, application de méthodes statistiques de prévision, interprétation humaine
• Transmission de la prévision à la clientèle dans une forme applicable au soutien à diverses activités (agriculture, transport, santé, prévisions environnementales, planification économique, etc)
• Vérification des prévisions a posteriori et évaluation de la performance du modèle

Exemple de la France

Météo-France utilise actuellement deux modèles numériques, tels deux boîtes imbriquées les unes dans les autres pour émettre ses bulletins. Le modèle mondial Arpège (Action de recherche petite échelle/grande échelle) produit des prévisions sur le monde entier avec une maille de 7,5 km sur la France pour une échéance de un à trois jours, mais moins précise ailleurs.

Depuis 2008, le modèle Arome (Application de la recherche à l'opérationnel à mésoéchelle) effectue des prévisions sur un domaine limité englobant la France avec une maille de 2,5 km au début, et de 1,3 km depuis 2015. Le calcul intègre toutes les heures et réajuste les prévisions à partir des informations des stations météorologiques, navires, bouées, avions, radar, satellites… Le modèle évalue aussi la fiabilité de la prévision^[4].

Principaux centres d'application

Bien qu'il y ait une croissance notable de l'application de la PNT avec des moyens relativement modestes, la PNT de pointe exige une infrastructure informatique considérable qui la place parmi les grands défis de l'informatique moderne. La mise en œuvre de la PNT est généralement confiée à des organisations gouvernementales ou même supra-gouvernementales. Les leaders mondiaux de la PNT sont en ce moment (par ordre alphabétique) :

• L'Allemagne (Deutscher Wetterdienst);
• Le Canada (Centre de recherche en prévision numérique (Canada) du Service météorologique du Canada);
• Le Centre européen de prévision météorologique à moyen terme (Opéré par un consortium de nations européennes);
• Les États-Unis (National Centers for Environmental Prediction (civil), Fleet Numerical Meteorology and Oceanography Center (en) (militaire));
• La France (Météo-France);
• Le Japon (Japan Meteorological Agency);
• Le Royaume-Uni (UK Met Office).

Il convient de remarquer que les grands opérateurs de centres de PNT, en plus de fournir des services de prévision du temps, font aussi une part importante de la recherche scientifique dans le domaine. Encore une fois, les questions d'infrastructure y sont pour quelque chose : le super-ordinateur étant en substance le laboratoire du chercheur en PNT. De plus, la proximité de la recherche et des opérations aide à accélérer la mise en pratique des innovations scientifiques.

Notes et références

Voir aussi

Bibliographie

• (en) Hagos S et LR Leung, « Large-Scale Environmental Variables and Transition to Deep Convection in Cloud Resolving Model Simulations: A Vector Representation », Journal of Advances in Modeling Earth Systems, vol. 4, n^o M11001,‎ 2012 (DOI 10.1029/2012MS000155)

Articles connexes

Liens externes

• Explication de la PNT, Centre météorologique canadien
• Prévision numérique du temps par Euromet
• La prévision du temps, Météo France
• PNT à MétéoSuisse
• Katia Chancibault, « La prévision numérique météorologique », Risques hydro-météorologiques, crues et inondations, Laboratoire d'études des Transferts en Hydrologie et Environnement (LTHE) (consulté le 23 avril 2011) [PDF]
• (en) The problem of Weather Prediction, as seen from the standpoints of Mechanics and Physics par Wilhelm Bjerknes dans le site de NOAA;
• (en) Peter Lynch du Met Éiriann, « Richardson's forecast: What went wrong? (Une analyse du premier essai de prévision de Richardson) », National Oceanic and Atmospheric Administration (NOAA),‎ juin 2004 (consulté le 30 décembre 2006) [PDF]

• Portail de la météorologie