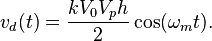Modulation d'amplitude
La modulation d'amplitude ou MA (AM en anglais) est une technique utilisée pour moduler un signal. Elle consiste en la multiplication du signal à moduler par un signal de fréquence plus élevée.
Définition
La modulation d'amplitude consiste à faire varier l'amplitude d'un signal de fréquence élevée, le signal porteur, en fonction d'un signal de plus basse fréquence, le signal modulant. Ce dernier est celui qui contient l'information à transmettre (voix, par exemple, recueillie par un microphone).
Allure du signal modulé
Le signal porteur xp(t) est de fréquence élevée (fréquence radio dépassant 100 kHz). Son allure est la suivante :

Le signal modulant xm(t) est lui de fréquence relativement faible (par exemple fréquence audio inférieure à 20 kHz) :

Le signal modulé (ou signal de sortie) y(t), a l'allure suivante (pour un taux de modulation de 50 %) :
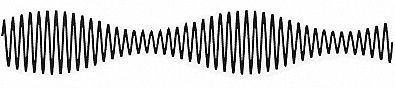
La figure suivante montre la différence entre la modulation en amplitude (AM) et la modulation en fréquence (FM).

Pour la modulation d'amplitude, il s'agit donc de faire varier l'amplitude de la porteuse en fonction du signal modulant, sans que cette variation dépasse l'amplitude de la porteuse avant modulation.
Modulation
Principe
La porteuse (avant modulation) est un signal sinusoïdal de fréquence fp relativement élevée :
où
- Ap est l'amplitude maximale du signal ;
- ωp = 2π fp est la pulsation du signal.
Supposons pour simplifier que le signal modulant soit périodique (sinusoïdal lui aussi), de fréquence nettement plus faible fm :
où
- Am est l'amplitude maximale du signal ;
- ωm = 2π fm est la pulsation du signal.
Supposons en outre que ce signal soit amplifié d'un facteur k lors de la modulation.
Le signal modulé est alors obtenu en ajoutant le signal de la porteuse et le produit de celui-ci par le signal modulant et le facteur k. Soit :
Ou encore, en posant h = kAm :
h est appelé indice de modulation. Cet indice doit rester inférieur ou égal à 1, sous peine de « surmodulation » (voir ci-dessous).
Dans l'expression suivante :
on voit le terme constant égal à Ap correspondant à ce qui est parfois appelé (abusivement) offset ou décalage.
Implémentation
Techniquement, la modulation s'effectue grâce à des circuits électroniques spécifiques (appelés modulateurs) :
- soit un amplificateur à gain variable dont la commande de gain est justement le signal modulant (auquel on a ajouté une composante continue[1] pour éviter la surmodulation (voir plus bas) ;
- soit en technologie DSP un multiplieur (de constante multiplicative k) et un additionneur :
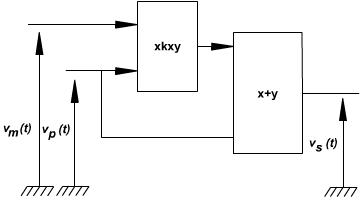
Dans les deux cas le signal de sortie est le même : celui obtenu en ajoutant le signal de la porteuse et son produit par le signal modulant et le facteur k.
Indice de modulation
L'indice de modulation (ou taux de modulation, ou profondeur de modulation) d'amplitude est la mesure de la variation d'amplitude par rapport à l'amplitude de la porteuse non modulée. On le définit par :
où Vm est l'amplitude maximale[2] du signal modulant.
L'indice de modulation d'amplitude est normalement compris entre 0 et 1 (autrement dit entre 0 % et 100 %) pour éviter la surmodulation (3e exemple de la figure ci-dessus). Les systèmes de transmission incorporent en général un circuit limiteur permettant d'éviter un tel dépassement.
Si h = 0,5, l'amplitude de la porteuse varie entre 50 % au-dessus et 50 % au-dessous de son niveau normal (autrement dit entre 50 % et 150 %). Pour h = 1, elle varie entre 0 % et 200 %. Ces deux exemples sont représentés dans la figure ci-dessous.

S'il n'y a pas de surmodulation la formule suivante permet de calculer l'indice de modulation en mesurant seulement les amplitudes maximales et minimales du signal modulé :
où
- Vmax est l'amplitude maximale du signal modulé ;
- Vmin est l'amplitude minimale du signal modulé.
Surmodulation
Si l'amplitude du signal modulant est supérieure au décalage (ceci peut arriver si l'on ajoute un offset avant la multiplication) le taux de modulation 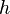 est supérieur à 1. On parle de surmodulation. La surmodulation est un peu différente suivant le type de démodulateur. Dans tous les cas cependant, le gros inconvénient de la surmodulation, c'est que la démodulation ne peut plus restituer correctement le signal transmis (modulant). Il y a donc distorsion de celui-ci.
est supérieur à 1. On parle de surmodulation. La surmodulation est un peu différente suivant le type de démodulateur. Dans tous les cas cependant, le gros inconvénient de la surmodulation, c'est que la démodulation ne peut plus restituer correctement le signal transmis (modulant). Il y a donc distorsion de celui-ci.
Dans le cas d'un modulateur DSP, le signal résultant étant alors de la forme suivante (avec inversion de phase là où il y a surmodulation) :
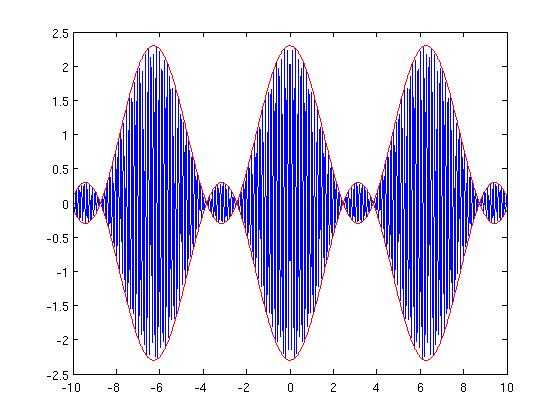
Dans le cas d'un modulateur par amplificateur à gain variable, l'amplitude devient nulle dans les zones où il y a surmodulation.
Spectre de fréquences
Le spectre de fréquences du signal modulé est un graphe présentant l'amplitude de chaque composante sinusoïdale du signal. En effet, tout signal périodique pouvant être décomposé en somme de fonctions sinusoïdales, le signal modulé est une somme de signaux sinusoïdaux, bien que l'expression trouvée précédemment soit un produit.
Reprenons-la et linéarisons-la :
Le spectre de fréquences est le suivant (l'amplitude des raies secondaires est Aph/2) :
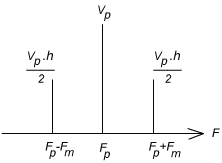
En pratique, le signal modulant balaye une certaine plage de fréquences [fm1, fm2]. L'allure du spectre de fréquences sera la suivante :
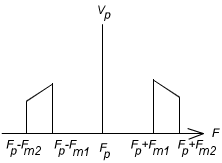
On voit donc ici que pour que deux signaux ne se brouillent pas mutuellement, il faut que les spectres ne se superposent pas. Il faut donc espacer suffisamment les fréquences des deux porteuses.
Démodulation
Une fois le signal reçu, il va falloir le démoduler pour pouvoir l'utiliser. On suppose que le signal reçu est de la forme :
Démodulation par DSP
Considérons le circuit DSP suivant :

Les signaux vs(t) et v0(t) sont appliqués aux deux entrées d'un multiplieur de constante k. v0(t) est un signal dont la fréquence est synchronisée avec celle de la porteuse.
Calculons u(t) :
u(t) est donc la somme de cinq signaux. u(t) va maintenant passer dans un filtre passe-bande, dont les fréquences de coupures seront choisies autour des fréquences du son audible. Ainsi à la sortie du filtre, toutes les composantes de fréquences trop faibles ou trop élevées seront supprimées et il ne restera que le signal :
On obtient ainsi le signal initial, avec une amplitude différente.
Démodulation par détection
Une simple diode redressant le signal et l'obligeant donc à être positif va faire que la valeur moyenne ne sera pas nulle mais suivra les variations du signal modulant. Un filtre passe-bas (condensateur + résistance par exemple) va alors permettre d'éliminer la composante haute fréquence et on retrouvera le signal initial.
Problème de la démodulation
En pratique, il sera impossible d'avoir un signal v0(t) parfaitement synchrone de la porteuse. En effet, les fluctuations de la fréquence, aussi minimes soient elles vont entrainer une détérioration du signal audible, appelée fading. La correction de ce problème passe par la mise en place d'une boucle à verrouillage de phase, qui permet d'ajuster au mieux la fréquence de v0(t).
Articles connexes
- Modulation de fréquence
- Modulation d'amplitude en quadrature de phase
- Radio AM
Notes et références
- ↑ Cette composante continue est appelée parfois offset.
- ↑ En pratique, le signal modulant n'est pas sinusoïdal. Son amplitude est donc elle-même variable et c'est la valeur max de cette amplitude qu'il faudra utiliser dans cette formule.
- Portail de l’électricité et de l’électronique
- Portail des télécommunications
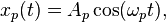
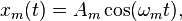
![\begin{align}
y(t)
&= x_{p}(t) + kx_{p}(t)x_{m}(t)\\
&= x_{p}(t)[1 + k x_{m}(t)]\\
&= A_{p}[1 + kA_{m} \cos(\omega_{m}t)] \cos(\omega_{p}t).
\end{align}](../i/m/c1916b3012259835586b8a4e6f63400d.png)
![y(t) = A_{p}[1 + h \cos(\omega_{m}t)] \cos(\omega_{p}t).](../i/m/a8aa8036c5467292abcad70acce3489d.png)
![y(t) = [A_{p} + hA_{p} \cos(\omega_{m}t)] \cos(\omega_{p}t),](../i/m/3372b3a9ecdfc3c3fe303b7062299e85.png)
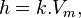
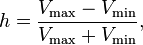
![\begin{align}
y(t)
&= A_{p}[1 + h \cos(\omega_{m}t)] \cos(\omega_{p}t)\\
&= A_{p} \cos(\omega_{p}t) + A_{p}h \cos(\omega_{m}t) \cos(\omega_{p}t)\\
&= A_{p} \cos(\omega_{p}t) + \frac{A_{p}h}{2} \cos[(\omega_{p}+\omega_{m})t] + \frac{A_{p}h}{2} \cos[(\omega_{p} - \omega_{m})t].
\end{align}](../i/m/35e5ee95092bad28891f8019cf839b57.png)
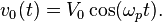
![\begin{align}
u(t)
&= kv_0(t)v_{s}(t)\\
&= kV_0 V_p[1 + h \cos(\omega_{m}t)] \cos^2(\omega_{p}t)\\
&= kV_0 V_p[1 + h \cos(\omega_{m}t)]\frac{1 + \cos(2\omega_{p}t)}{2}\\
&= \frac{kV_0 V_{p}}{2}[1 + h \cos(\omega_{m}t) + \cos(2\omega_{p}t) + \cos(2\omega_{p}t)h \cos(\omega_{m}t)]\\
&= \frac{kV_0 V_{p}}{2}\left[1 + h \cos(\omega_{m}t) + \cos(2\omega_{p}t) + \frac{1}{2}h[\cos(2\omega_{p}t + \omega_mt) + \cos(2\omega_{p}t - \omega_{m}t)]\right]\! .
\end{align}](../i/m/afb14182449e81418c995799806355e0.png)