Mathématiques financières

Les mathématiques financières sont une branche des mathématiques appliquées ayant pour but la modélisation, la quantification et la compréhension des phénomènes régissant les opérations financières d'une certaine durée (emprunts et placements / investissements) et notamment les marchés financiers. Elles font jouer le facteur temps et utilisent principalement des outils issus de l'actualisation, de la théorie des probabilités, du calcul stochastique, des statistiques et du calcul différentiel.

Antériorité

L'actualisation et l'utilisation des intérêts composés et des probabilités remontent à plusieurs siècles.

Cela dit Louis Bachelier, par sa thèse intitulée Théorie de la spéculation en 1900, est considéré comme le fondateur des mathématiques financières appliquées aux marchés. La théorie moderne des marchés financiers remonte au MEDAF et à l'étude du problème d'évaluation des options et autres contrats financiers dérivés dans les années 1950-1970.

Nature aléatoire des marchés

L'observation empirique du cours des actifs financiers montre que ceux-ci ne sont pas déterminés de façon certaine par leur histoire. En effet, les nombreuses opérations d'achat ou de vente ne sont pas prévisibles, elles font souvent intervenir des éléments nouveaux. Le cours de l'actif financier est donc souvent représenté par un processus stochastique. Benoit Mandelbrot a établi par des considérations statistiques qu'un modèle aléatoire ordinaire, par exemple gaussien, ne convient pas. L'aléa reste cependant souvent modélisé par un mouvement brownien^[1], bien que des modèles plus élaborés (par exemple, le modèle de Bates) tiennent compte de la non-continuité des cours (présence de sauts (gaps) dus à des chocs boursiers), ou de la non-symétrie des mouvements à la baisse et à la hausse.

Hypothèse de non arbitrage

L'une des hypothèses fondamentales des modèles usuels est qu'il n'existe aucune stratégie financière permettant, pour un coût initial nul, d'acquérir une richesse certaine dans une date future. Cette hypothèse est appelée absence d'opportunités d'arbitrage. Elle est justifiée théoriquement par l'unicité des prix caractérisant un marché en concurrence pure et parfaite. Pratiquement, il existe des arbitrages qui disparaissent très rapidement du fait de l'existence d'arbitragistes, acteurs sur les marchés dont le rôle est de détecter ce type d'opportunités et d'en profiter. Ces acteurs créent alors normalement une force qui tend à faire évoluer le prix de l'actif vers son prix de non-arbitrage. Ces opérations d'arbitrage sont effectuées instantanément et ne doivent pas être confondues avec des opérations par lesquelles un investisseur joue le retour à moyen ou long terme d'un actif vers des fondamentaux historiques. En conséquence, l'existence de bulles et de krachs ne remet pas en cause cette hypothèse (mais elle remet en revanche en cause l'hypothèse d'efficience des marchés).

Hypothèse de complétude des marchés

Une autre hypothèse, beaucoup plus remise en question, est que tout flux à venir peut être répliqué exactement, et quel que soit l'état du monde, par un portefeuille d'autres actifs bien choisis. Les modèles ne comprenant pas les hypothèses de non arbitrage et de complétude des marchés sont dits modèles de marchés imparfaits.

Probabilité risque-neutre

Une des conséquences des hypothèses de non arbitrage et de complétude des marchés est l'existence et l'unicité à équivalence près d'une mesure de probabilité dite probabilité martingale ou « probabilité risque-neutre » telle que le processus des prix actualisés des actifs ayant une source de risque commune est une martingale sous cette probabilité. Cette probabilité peut s'interpréter comme celle qui régirait le processus de prix des sous-jacents de ces actifs si l'espérance du taux de rendement de ceux-ci était le taux d'intérêt sans risque (d'où le terme risque-neutre: aucune prime n'est attribuée à la prise de risque).

Un processus stochastique est une martingale par rapport à un ensemble d'information si son espérance en date t conditionnelle à l'information disponible en date s < t est égale à la valeur du processus en date s, c'est-à-dire qu'un processus A(u) est une martingale si l'espérance conditionnelle de A(t) par rapport à la filtration F(s) est A(s) (i.e : $\mathbb{E}\left[A_t|\mathcal{F}_s\right]=A_s$ ).

Le problème d'évaluation des produits dérivés

L'évaluation (on dit aussi pricing ou, à tort, « valorisation » qui signifie « augmenter la valeur ») des produits dérivés se ramène souvent au calcul du prix aujourd'hui d'un actif dont on ne connaît le prix qu'à une date future. Il se ramène donc au calcul d'une espérance conditionnelle. Le modèle Black-Scholes est un exemple de solution analytique au problème d'évaluation des options d'achat (call) ou de vente (put) d'un actif sous-jacent. Dans le cas d'un call, le problème s'écrit :

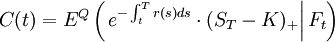$C(t) = E^Q\left(\left.e^{-\int_{t}^T r(s)ds}\cdot(S_T - K)_+\right| F_{t}\right)$ ,

où 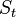$S_t$ est le cours de l'actif, 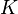$K$ est le prix d'exercice (ou Strike), $r(s)$ est le taux d'intérêt instantané sans risque à la date s, 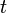$t$ est la date « d'aujourd'hui », 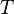$T$ est la maturité de l'option, c’est-à-dire la date à laquelle la décision d'exercice peut être prise.

La formule de Black et Scholes est un exemple de solution analytique à ce problème, sous des hypothèses restrictives sur la dynamique du sous-jacent. Voir aussi option.

Une obligation convertible peut s'évaluer comme un lot comprenant une option d'achat et une obligation classique.

Taux d'intérêt et dérivés de taux d'intérêt

Les modèles simples supposent que le taux d'intérêt, c'est-à-dire le loyer de l'argent est constant. Cette hypothèse est centrale, car sous l'hypothèse d'absence d'opportunités d'arbitrage, un portefeuille non risqué rapporte ce taux d'intérêt. Or cette approximation n'est évidemment plus admissible dès que le cours de l'actif est essentiellement lié au niveau du taux d'intérêt (par exemple, le cours des obligations à taux variable, des swaptions…, ne peuvent être expliqués par un modèle à taux d'intérêt fixe).

On modélisera donc le taux d'intérêt par un processus aléatoire, auquel on demandera :

d'être au mieux compatible avec l'ensemble des courbes des taux observables ;
d'avoir des propriétés réalistes, comme de ne pas autoriser des taux négatifs, de rendre compte de l'effet de retour à la moyenne (mean reversion)…

Les travaux de Vasicek ont permis d'exhiber un processus, dérivé du processus d'Ornstein-Uhlenbeck, cohérent, dont le loyer de l'argent ne dépend que du taux instantané (overnight) mais autorisant des taux négatifs. Des modèles plus élaborés (processus CIR…), faisant partie de la famille dite des modèles affines de taux court, ont permis de remédier à cette lacune, mais ne satisfont pas vraiment les spécialistes du fait de la difficulté d'interprétation financière des paramètres de diffusion et de leur incapacité à épouser exactement la courbe des taux zéro-coupon spot. Heath, Jarrow et Morton ont proposé une famille de modèles cohérents, dont la dynamique ne dépend que d'une fonction facilement interprétable (la volatilité du taux forward), et capables de rendre compte de n'importe quelle courbe de taux donnée. Des modèles dits de marché (BGM ou Libor Forward) connaissent un certain succès dans l'explication du prix des caps et des floors.

Toutefois, à la différence du marché des dérivés d'options où le modèle de Black et Scholes, plus ou moins arrangé pour le débarrasser de ses imperfections (volatilité constante, taux d'intérêt constant…) occupe une place prépondérante, aucun modèle de taux ne fait l'unanimité des spécialistes. Les taux d'intérêts sont en effet soumis à des pressions exogènes très importantes, qui rendent caduques très rapidement toutes les calibrations possibles. À l'heure actuelle, les publications et les recherches à ce sujet sont abondantes.

Dérivés de crédit

Les dérivés de crédit sont des produits dérivés dont les flux dépendent d'événements de crédits intervenant sur un sous-jacent. Ces produits servent à prévenir la dégradation de la qualité de signature d'une contrepartie, c'est-à-dire son aptitude à assumer ses obligations de paiement (« CDS » ou Credit default swap, « CLN » ou « Credit linked Notes »). Ils peuvent servir également à améliorer la qualité de signature d'une partie d'un panier d'actifs (« CDOs » ou « Collateralized debt obligations »).

Dérivés climatiques

Article détaillé : Dérivé climatique.

Les dérivés climatiques sont des produits financiers dont les flux dépendent d'un événement totalement indépendant de la structure des marchés financiers, lié à un événement climatique. Par exemple, un produit peut assurer à son détenteur une rente dans le cas où la température relevée en un lieu fixé par contrat dépasse ou reste en dessous d'une température de référence considérée comme normale. Ces produits — récents — ont pour vocation de permettre à des entreprises touristiques ou agricoles de se prémunir contre des aléas climatiques. Ils s'apparentent donc à des produits d'assurance, négociés directement sur les marchés financiers.

Au-delà du pricing de dérivés

Si les mathématiques financières se sont développées autour de la question du pricing des produits dérivés sur tous les types de sous-jacent, de nombreux autres sujets font aujourd'hui partie des mathématiques financières. Il en est ainsi de l'étude de la microstructure de marché, de la question de l'exécution optimale ou encore des stratégies à haute-fréquence, notamment pour le market making.

Notes et références

↑ Les caprices de marchés financiers : régularité et turbulences, Conférence de Jean-Philippe Bouchaud à l'Université de tous les savoirs, 2000

Voir aussi

Bibliographie

Pierre Bonneau, Mathématiques financières, Coll. Economie, Paris, Dunod, 1980.
Jean-Marcel Dalbarade, Mathématiques des marchés financiers, Ed. Eska, 2005, ISBN 2-7472-0846-X.
Benoît Mandelbrot & Richard Hudson, Une approche fractale des marchés, éditions Odile Jacob, 2005
Mathieu Le Bellac & Arnaud Viricel, Mathématiques des marchés financiers: Modélisation du risque et de l'incertitude, Ed. EDP Sciences, 2012.
Gustave Bessière, Contre l'inflation et ses risques Dunod Paris 1933

Liens externes

(fr) Cours du Dea de Probabilité, option finance du professeur Nicole El Karoui.
(en) Exemples d'application en ligne en finance quantitative (pricing d'options à travers plusieurs méthodes) pricing-option.com Christophe Rougeaux.

Portail de la finance
Portail des mathématiques

This article is issued from Wikipédia - version of the Monday, October 26, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.