Méthode de Monte-Carlo par chaînes de Markov
 |
Cet article est une ébauche concernant les probabilités et la statistique. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
Consultez la liste des tâches à accomplir en page de discussion. |
Les méthodes de Monte-Carlo par chaînes de Markov, ou méthodes MCMC pour Markov chain Monte Carlo, sont une classe de méthodes d'échantillonnage à partir de distributions de probabilité. Ces méthodes de Monte-Carlo se basent sur le parcours de chaînes de Markov qui ont pour lois stationnaires les distributions à échantillonner.
Certaines méthodes utilisent des marches aléatoires sur les chaînes de Markov (Algorithme de Metropolis-Hastings, Échantillonnage de Gibbs), alors que d'autres algorithmes, plus complexes, introduisent des contraintes sur les parcours pour essayer d'accélérer la convergence (Monte Carlo Hybride, Surrelaxation successive)
Ces méthodes sont notamment appliquées dans le cadre de l'inférence bayésienne.
Approche intuitive
On se place dans un espace vectoriel 
de dimension finie n. On veut générer aléatoirement des vecteurs 
suivant une distribution de probabilité π. On veut donc avoir une suite de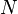 
vecteurs 
telle que la distribution des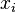 
approche π.
Les méthodes de Monte-Carlo par chaînes de Markov consistent à générer un vecteur 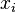uniquement à partir de la donnée du vecteur 
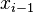; c'est donc un processus « sans mémoire », ce qui caractérise les chaînes de Markov. Il faut donc trouver un générateur aléatoire avec une distribution de probabilité 
qui permette de générer 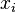à partir de 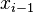. On remplace ainsi le problème de génération avec une distribution π par 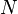problèmes de génération avec des distributions 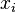, que l'on espère plus simples.
Principe
On veut simuler une loi Ï€ sur un espace d'états général (Ω ; Æ). Une transition sur (Ω ; Æ) est une application P : (Ω ; Æ) → [0 ; 1] telle que P(·, A) pour tout AâˆˆÆ est mesurable et P(x,·) pour tout x∈Ω est une probabilité sur (Ω ; Æ). Soit X = (Xk,k∈ℕ) une chaîne de Markov homogène de transition P et de loi initiale X0 ~ v, on note Pv la loi de la chaîne X.
Pour simuler Ï€, on veut savoir construire une transition P telle que ∀ v, vPk → π, avec convergence en norme en variation totale ∥μ∥ = supAâˆˆÆ Î¼(A) − infAâˆˆÆ Î¼(A). La chaîne de transition P est ergodique.
Convergence d'une chaîne de Markov — Si une transition P est π-réductible, π-invariante, apériodique, Harris-récurrente, alors ∀x, Pk(x,·) →k→∞ π.
La dernière condition, délicate, est satisfaite dans les cas de l'échantillonnage de Gibbs et de l'algorithme de Metropolis-Hastings.
Voir aussi
D'autres échantillonnages de distribution
- Méthode de la transformée inverse
- Méthode de rejet
- Échantillonnage préférentiel
Bibliographie
- (en) George Casella et Christian Robert, Introducing Monte Carlo Methods with R, Springer-Verlag, coll. « Use R! Series »,‎ (ISBN 978-1441915757)
- (en) Christian Robert et George Casella, Monte Carlo Statistical Methods, Springer-Verlag, coll. « Springer Texts in Statistics »,‎
- (en) Christophe Andrieu, An Introduction to MCMC for Machine Learning, Kluwer Academic Publishers,‎ (lire en ligne)
- Portail des probabilités et de la statistique