Espace symétrique

Cet article est une ébauche concernant la géométrie.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
Consultez la liste des tâches à accomplir en page de discussion.

En mathématiques, et plus spécifiquement en géométrie différentielle, un espace riemannien symétrique est une variété riemannienne qui, en chaque point, admet une isométrie involutive dont ce point est un point fixe isolé. Plus généralement, un espace symétrique est une variété différentielle munie, en chaque point, d'une involution, le tout vérifiant certaines conditions. Lorsqu'il n'y pas de risque de confusion, les espaces riemanniens symétriques sont appelés espaces symétriques. Les espaces symétriques connexes sont des espaces homogènes de groupes de Lie.

Les espaces des géométries euclidiennes et non euclidiennes sont naturellement des espaces riemanniens symétriques. La plupart des espaces homogènes usuels de la géométrie différentielles sont soit des espaces symétriques (riemanniens ou non) soit ce que l'on appelle variétés de drapeaux généralisés (généralisation des espaces projectifs, des grassmanniennes, des quadriques projectives).

Dans ce cas riemannien, ces espaces ont été définis et classifiés pour la première fois par Élie Cartan. Ils constituent un cadre naturel pour généraliser l'analyse harmonique classique sur les sphères.

Espaces riemanniens symétriques

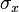En géométrie riemannienne, une variété riemannienne (M, g) est dite localement symétrique si, localement, autour de chaque point $x$ , il existe une symétrie $\sigma_x$ qui inverse les géodésiques issues de $x$ et qui est une isométrie (locale).

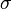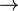Un espace riemannien symétrique est une variété riemannienne localement symétrique dont les symétries peuvent se prolonger à tout l'espace. De manière équivalente, une variété riemannienne (M,g) est dite symétrique lorsque, pour tout point x de M, il existe une isométrie $\sigma$ _x:M $\rightarrow$ M vérifiant :

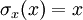$\sigma_x(x)=x$ ;
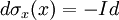$d\sigma_x(x)=-Id$ .

Cette isométrie 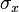$\sigma_x$ est appelée la symétrique en x.

Propriétés remarquables

Tout espace riemannien symétrique est une variété riemannienne géodésiquement complète (en), donc complète en vertu du théorème de Hopf-Rinow.
Il existe une et une unique symétrie en x.
Le tenseur de courbure d'une variété riemannienne est parallèle.

Exemples d'espaces symétriques

Les espaces euclidiens sont des espaces riemanniens symétriques.
Les sphères, les espaces elliptiques (réels, complexes et quaternioniens) sont des espaces symétriques, de rang 1.
Les variétés riemanniennes de courbure sectionnelle constante sont des espaces localement symétriques.
Les espaces hyperboliques (réels, complexes et quaternioniens) sont des espaces symétriques de rang 1.
Les espaces d'Heisenberg sont des espaces symétriques.

Classification des espaces riemanniens symétriques

Espaces riemanniens symétriques irréductibles simplement connexes de type compact

Voici les espaces riemanniens symétriques irréductibles simplement connexes de type compact dont le groupe est classique

SU(n)/SO(n)
SU(2n)/Sp(n)
SU(p + q)/S(U(p) × U(q))
SO(p + q)/(SO(p) × SO(q))
Sp(p + q)/(Sp(p) × Sp(q))
Sp(n)/U(n)
SO(2n)/U(n)
SU(n)
Sp(n)
Spin(n)

Espaces riemanniens symétriques irréductibles simplement connexes de type non compact

Voici les espaces riemanniens symétriques irréductibles simplement connexes de type compact dont le groupe est classique

SL(n, R)/SO(n)
SL(n, H)/Sp(n)
SU(p, q)/S(U(p) × U(q))
SO(p, q)/(SO(p) × SO(q))
Sp(p, q)/(Sp(p) × Sp(q))
Sp(2n, R)/U(n)
O(n, H)/U(n)
SL(n, C)/SU(n)
Sp(2n, C)/Sp(n)
SO(n, C)/SO(n)

Espaces hermitiens symétriques

R-espaces symétriques

Classification

Voici la classification des R-espaces symétriques de groupes de Lie classiques. Ils admettent tous une interprétation géométrique simple. Par grassmannienne lagrangienne, il faut ici entendre la variété des sous-espaces vectoriels de dimension n qui sont totalement isotropes, c'est-à-dire sur lesquels les formes s'annulent identiquement.

Grassmanniennes réelles, complexes et quaternioniennes d'indices p:
- U(p + q)/S(U(p) × U(q));
- SO(p + q)/S(O(p) × O(q));
- Sp(p + q)/(Sp(p) × Sp(q)).
Grassmanniennes lagrangiennes de formes quadratiques réelles, hermitiennes complexes et quaternioniennes de signature (n, n) (une des deux composantes connexes dans le cas réel):
- (SO(n) × SO(n))/SO(n);
- (U(n) × U(n))/U(n);
- (Sp(n) × Sp(n))/Sp(n).
Grassmanniennes lagrangiennes de formes bilinéaires alternées réelles et complexes en dimension 2n:
- U(n)/O(n);
- Sp(n)/U(n).
Grassmanniennes lagrangiennes des formes quadratiques complexes (une des deux composantes connexes en fait) et des formes antihermitiennes quaternioniennes en dimension 2n:
- SO(2n)/U(n);
- U(2n)/Sp(n).
Quadriques projectives propres réelles et complexes:
- (O(p) × O(q))/(O(1) × O(p - 1) × O(q - 1)).
- SO(n)/(SO(2) × SO(n - 2)).

Ces interprétations ne sont pas intrinsèques : elles dépendent du système de coordonnées choisis. Par exemple, la grassmannienne d'indice p d'un espace vectoriel réel n'est pas intrinsèquement un espace symétrique, mais le devient si l'espace vectoriel est muni d'un produit scalaire euclidien.

Espaces symétriques généraux

Classification des espaces symétriques simples

Il y a (localement) 54 familles d'espaces symétriques simples de groupes de Lie classiques simples. Il y a d'abord dix familles d'espaces symétriques simples complexes (de la forme G/H, où G et H sont des groupes de Lie complexes), et les versions réelles de ces espaces symétriques complexes. Chacun des dix tableaux correspond à un famille d'espaces symétriques complexes, et la première ligne est celle de l'espace symétrique complexe correspondant. Lorsqu'il y a deux colonnes dans un tableau, la première est celle d'espaces symétriques simples, et la seconde est celle d'espaces symétriques « réductifs » liés à ceux de la première colonne : ils ont une interprétation géométrique parfois plus simple. Notons que l'espace symétrique de la seconde colonne peut être canoniquement isomorphe à celui de la première colonne.

SL(n, C)	GL(n, C)
SL(n, R)	GL(n, R)
SL(n, H)	GL(n, H)
SU(p, q)	U(p, q)
SL(n, C)/SL(n, R)	GL(n, C)/GL(n, R)
SL(2n, C)/SL(n, H)	GL(2n, C)/GL(n, H)
SL(p + q, C)/SU(p, q)	GL(p + q, C)/U(p, q)

SL(n, C)/SO(n, C)	GL(n, C)/O(n, C)
SU(p, q)/SO(p, q)	U(p, q)/O(p, q)
SL(p + q, R)/SO(p,q)	GL(p + q, R)/O(p,q)
SL(n, H)/O(n, H)	GL(n, H)/O(n, H)
U(n, n)/O(n, H)	-

SL(2n, C)/Sp(2n, C)	GL(2n, C)/Sp(2n, C)
SL(2n, R)/Sp(2n, R)	GL(2n, C)/Sp(2n, R)
SL(p + q, H)/Sp(p, q)	GL(p + q, H)/Sp(p, q)
SU(n, n)/Sp(2n, R)	U(n, n)/Sp(2n, R)
SU(2p, 2q)/Sp(p, q)	U(2p, 2q)/Sp(p, q)

SL(p + q, C)/S(GL(p, C) × GL(q, C))	GL(p + q, C)/(GL(p, C) × GL(q, C))
SL(p + q, R)/S(GL(p, R) × GL(q, R))	GL(p + q, R)/(GL(p, R) × GL(q, R))
SL(p + q, H)/S(GL(p, H) × GL(q, H))	GL(p + q, H)/(GL(p, H) × GL(q, H))
SU(n, n)/GL^±(n, C)	U(n, n)/GL(n, C)
SU(p + q, r + s)/S(U(p, r) × U(q, s))	U(p + q, r + s)/(U(p, r) × U(q, s))
SL(2n, R)/SL*(n, C)	GL(2n, R)/GL(n, C)
SL(n, H)/SL*(n, C)	GL(n, H)/GL(n, C)

SO(n, C)	O(n, C)
SO₀(p, q)	O(p, q)
O(n, H)	-
SO(p + q, C)/SO(p, q)	O(p + q, C)/O(p, q)
SO(2n, C)/O(n, H)	O(2n, C)/O(n, H)

SO(p + q, C)/S(O(p, C) × O(q, C))	O(p + q, C)/(O(p, C) × O(q, C))
SO(p + q, r + s)/S(O(p, r) × O(q, s))	O(p + q, r + s)/(O(p, r) × O(q, s))
O(p + q, H)/(O(p, H) × O(q, H))	-
SO₀(n, n)/O(n, C)	O(n, n)/O(n, C)
O(n, H)/O(n, C)	-

SO(2n, C)/GL(n, C)	O(2n, C)/GL(n, C)
SO₀(n, n)/GL⁺(n, R)	O₀(n, n)/GL(n, R)
O(2n, H)/GL(n, H)	-
SO₀(2p, 2q)/U(p, q)	O(2p, 2q)/U(p, q)
O(p + q, H)/U(p, q)	-

Sp(2n, C)

Sp(2n, R)

Sp(p, q)

Sp(2n, C)/Sp(2n, R)

Sp(2p + 2q, C))/Sp(p, q)

Sp(2p + 2q, C)/(Sp(2p, C) × Sp(2q, C)

Sp(2p + 2q, R)/(Sp(2p, R) × Sp(2q, R)

Sp(p + q, r + s)/(Sp(p, r) × Sp(q, s))

Sp(4n)/Sp(2n, C)

Sp(n, n)/Sp(2n, C)

Sp(2n, C)/GL(n, C)

Sp(2n, R)/GL(n, R)

Sp(n, n)/GL(n, H)

Sp(2p + 2q, R)/U(p, q)

Sp(p + q)/U(p, q)

Historique

La théorie et la classification des espaces riemanniens symétriques sont l'œuvre d'Élie Cartan. La classification des espaces symétriques semi-simples non compacts est due à Marcel Berger.

Bibliographie

Articles

M. Berger, Sur les groupes d'holonomie des variétés riemanniennes non symétriques, 1953.
M. Berger, Structure et classification des espaces homogènes symétriques à groupe d'isométrie semi-simple, 1955.
M. Berger, Les espaces symétriques non compacts, 1957.
M. Berger, Sur quelques variétés d'Einstein compactes, 1962.

Livres

(en) Besse, Einstein manifolds (ISBN 0-387-15279-2).
(en) S. Helgason (de), Differential geometry, Lie groups, and symmetric spaces, Academic Press, 1978 (ISBN 0-8218-2848-7). Le livre de référence sur les espaces symétriques.

Voir aussi

Groupe de Lie
Algèbre de Lie
Décomposition de Cartan

Portail des mathématiques
Portail de la géométrie

This article is issued from Wikipédia - version of the Tuesday, November 05, 2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.