Dioïde
 |
Cet article est une ébauche concernant les mathématiques. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
|
En mathématiques et en informatique, un dioïde est un demi-anneau dans lequel le préordre défini par l'addition est une relation d'ordre.
Définition
Soit D un ensemble muni d'un opérateur binaire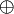 
, nommé addition, d'un opérateur binaire 
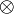, nommé produit, et dans lequel sont spécifiés deux éléments distincts, notés 0 et 1.
On note ≤ le préordre défini par l'opérateur 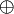, c'est-à-dire que 
.
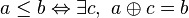On dit que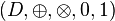 
est un dioïde si :
-
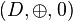est un monoïde commutatif ; -
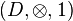est un monoïde ; - 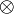est distributif par rapport à ;
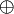- 0 est un élément absorbant pour 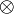, c'est-à-dire que
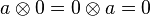; - la relation ≤ est une relation d'ordre, c'est-à-dire que
.
Si l'on omet le dernier point, la structure définie est un demi-anneau.
Le nom de dioïde provient du fait qu'il combine deux monoïdes, comme tout demi-anneau (en particulier tout anneau). Le dioïde et l'anneau sont tous deux des demi-anneaux, mais sont exclusifs l'un de l'autre.
Dioïde idempotent
Le dioïde idempotent est la classe de dioïdes la plus utilisée.
Il se caractérise le fait que tout élément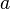 
est idempotent pour , c'est-à-dire que 
.
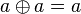Par exemple,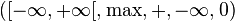 
est un dioïde idempotent.
Tout demi-anneau idempotent est un dioïde.
Il s'agit de prouver que la relation de préordre est un ordre.
Si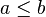 
alors il existe c tel que
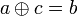, d'où
.
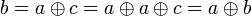De même, si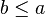 
alors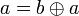 
. Par conséquent, si 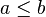et 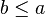, alors en utilisant la commutativité de 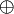on obtient
.
Les demi-anneaux idempotents sont donc exactement les dioïdes idempotents.
Référence
Michel Gondran et Michel Minoux, Graphes, dioïdes et semi-anneaux, Paris, Tec & Doc, (ISBN 2-7430-0489-4)
- Portail des mathématiques