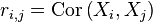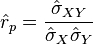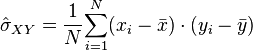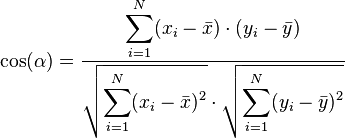Corrélation (statistiques)
En probabilités et en statistiques, étudier la corrélation entre deux ou plusieurs variables aléatoires ou statistiques numériques, c’est étudier l'intensité de la liaison qui peut exister entre ces variables.
Le type le plus simple de liaison est la relation affine. Dans le cas de deux variables numériques, elle se calcule à travers une régression linéaire. La mesure de la corrélation linéaire entre les deux se fait alors par le calcul du coefficient de corrélation linéaire, noté r. Ce coefficient est égal au rapport de leur covariance et du produit non nul de leurs écarts types. Le coefficient de corrélation est compris entre -1 et 1[1].
Le fait que deux variables soient « fortement corrélées » ne démontre pas qu'il y ait une relation de causalité entre l'une et l'autre. Le contre-exemple le plus typique est celui où elles sont en fait liées par une causalité commune. Cette confusion est connue sous l'expression Cum hoc ergo propter hoc.
Histoire
La corrélation est un concept issu de la biologie. C'est par le biais des travaux de Francis Galton que la corrélation devient un concept statistique. Toutefois pour Galton, la notion de corrélation n'est pas définie précisément et il l'assimile dans un premier temps à la droite de régression d'un modèle de régression linéaire[2].
C'est ensuite Karl Pearson qui propose en 1896 une formule mathématique pour la notion de corrélation et un estimateur de cette grandeur[2].
La corrélation est introduite en économie avec l'ouvrage de Bowley Elements of Statistics en 1902[3] et l'intervention de George Udny Yule en 1909. Yule introduit notamment la notion de corrélation partielle[4],[2].
L'usage du coefficient de corrélation a suscité de vives controverses. Par exemple Maurice Fréchet s'y est vivement opposé en montrant les difficultés d'interprétation de ce paramètre[5],[2].
Droite de régression
Calculer le coefficient de corrélation entre 2 variables numériques revient à chercher à résumer la liaison qui existe entre les variables à l'aide d'une droite. On parle alors d'un ajustement linéaire.
Comment calculer les caractéristiques de cette droite ? En faisant en sorte que l'erreur que l'on commet en représentant la liaison entre nos variables par une droite soit la plus petite possible. Le critère formel le plus souvent utilisé, mais pas le seul possible, est de minimiser la somme de toutes les erreurs effectivement commises au carré. On parle alors d'ajustement selon la méthode des moindres carrés ordinaires. La droite résultant de cet ajustement s'appelle une droite de régression. Plus la qualité globale de représentation de la liaison entre nos variables par cette droite est bonne, et plus le coefficient de corrélation linéaire associé l'est également. Il existe une équivalence formelle entre les deux concepts.
Coefficient de corrélation linéaire de Bravais-Pearson
Définition
Le coefficient de corrélation entre deux variables aléatoires réelles X et Y ayant chacune une variance (finie[6]), noté Cor(X,Y) ou parfois 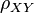 ou simplement
ou simplement 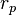 , est défini par
, est défini par
où 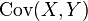 désigne la covariance des variables X et Y,
désigne la covariance des variables X et Y, 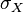 et
et 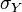 leurs écarts types.
leurs écarts types.
De manière équivalente
Matrice de corrélation
La matrice de corrélation d'un vecteur de p variables aléatoires 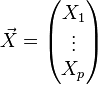 dont chacune possède une variance (finie), est la matrice carrée dont le terme générique est donné par :
dont chacune possède une variance (finie), est la matrice carrée dont le terme générique est donné par :
Les termes diagonaux de cette matrice sont égaux à 1, elle est symétrique, semi-définie positive et ses valeurs propres sont positives ou nulles.
Estimation
Partant d’un échantillon 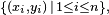 de réalisations indépendantes de deux variables X et Y, un estimateur non-biaisé du coefficient de corrélation est donné par
de réalisations indépendantes de deux variables X et Y, un estimateur non-biaisé du coefficient de corrélation est donné par
avec
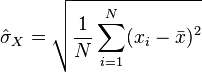 et
et 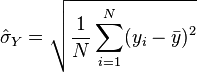
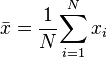 et
et 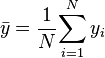
qui sont respectivement des estimateurs de la covariance, des écarts-type et des espérances des variables X et Y.
Remarques
- Numériquement,
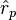 est compris dans [-1, 1] : c’est une conséquence de l’inégalité triangulaire.
est compris dans [-1, 1] : c’est une conséquence de l’inégalité triangulaire. - Les deux séries ne sont pas linéairement corrélées si
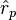 est nul. Les deux séries sont d'autant mieux corrélées que
est nul. Les deux séries sont d'autant mieux corrélées que 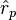 est proche de 1 ou de -1.
est proche de 1 ou de -1. - Appliqué à une matrice de corrélation, le test de sphéricité de Bartlett permet de juger si les coefficients extra-diagonaux sont globalement différents de zéro.
Interprétation

| Corrélation | Négative | Positive |
|---|---|---|
| Faible | de -0,5 à 0,0 | de 0,0 à 0,5 |
| Forte | de −1,0 à −0,5 | de 0,5 à 1,0 |
Il est égal à 1 dans le cas où l'une des variables est une fonction affine croissante de l'autre variable, à -1 dans le cas où une variable est une fonction affine et décroissante. Les valeurs intermédiaires renseignent sur le degré de dépendance linéaire entre les deux variables. Plus le coefficient est proche des valeurs extrêmes -1 et 1, plus la corrélation entre les variables est forte ; on emploie simplement l'expression « fortement corrélées » pour qualifier les deux variables. Une corrélation égale à 0 signifie que les variables ne sont pas corrélées.
Le coefficient de corrélation n’est pas sensible aux unités de chacune des variables. Ainsi, par exemple, le coefficient de corrélation linéaire entre l’âge et le poids d’un individu sera identique que l’âge soit mesuré en semaines, en mois ou en années.
En revanche, ce coefficient de corrélation est extrêmement sensible à la présence de valeurs aberrantes ou extrêmes (ces valeurs sont appelées des « déviants ») dans notre ensemble de données (valeurs très éloignées de la majorité des autres, pouvant être considérées comme des exceptions).
Plusieurs auteurs ont proposé des directives pour l'interprétation d'un coefficient de corrélation. Cohen (1988)[7], a observé, toutefois, que tous ces critères sont à certains égards arbitraires et ne doivent pas être trop strictement observés. L'interprétation d'un coefficient de corrélation dépend du contexte et des objectifs. Une corrélation de 0,9 peut être très faible si l'on vérifie une loi physique en utilisant des instruments de qualité, mais peut être considérée comme très élevée dans les sciences sociales où il peut y avoir une contribution plus importante de facteurs de complication.
Interprétation géométrique
Les deux séries de valeurs 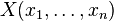 et
et 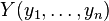 peuvent être considérées comme des vecteurs dans un espace à n dimensions. Remplaçons-les par des vecteurs centrés :
peuvent être considérées comme des vecteurs dans un espace à n dimensions. Remplaçons-les par des vecteurs centrés :
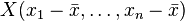 et
et 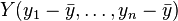 .
.
Le cosinus de l'angle α entre ces vecteurs est donné par la formule suivante (produit scalaire normé) :
Donc 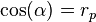 , ce qui explique que
, ce qui explique que 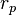 est toujours compris entre -1 et 1.
est toujours compris entre -1 et 1.
Le coefficient de corrélation n’est autre que le cosinus de l'angle α entre les deux vecteurs centrés !
- Si r = 1, l’angle α = 0, les deux vecteurs sont colinéaires (parallèles).
- Si r = 0, l’angle α = 90°, les deux vecteurs sont orthogonaux.
- Si r = -1, l’angle α vaut 180°, les deux vecteurs sont colinéaires de sens opposé.
- Plus généralement :
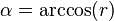 , où
, où 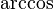 est la réciproque de la fonction cosinus.
est la réciproque de la fonction cosinus.
Bien sûr, du point vue géométrique, on ne parle pas de « corrélation linéaire » : le coefficient de corrélation a toujours un sens, quelle que soit sa valeur entre -1 et 1. Il nous renseigne de façon précise, non pas tant sur le degré de dépendance entre les variables, que sur leur distance angulaire dans l’hypersphère à n dimensions.
Dépendance
Attention, il est toujours possible de calculer un coefficient de corrélation (sauf cas très particulier) mais un tel coefficient n'arrive pas toujours à rendre compte de la relation qui existe en réalité entre les variables étudiées. En effet, il suppose que l'on essaye de juger de l'existence d'une relation linéaire entre nos variables. Il n'est donc pas adapté pour juger de corrélations qui ne seraient pas linéaires et non linéarisables. Il perd également de son intérêt lorsque les données étudiées sont très hétérogènes puisqu'il représente une relation moyenne et que l'on sait que la moyenne n'a pas toujours un sens, notamment si la distribution des données est multi modale.
Si les deux variables sont totalement indépendantes, alors leur corrélation est égale à 0. La réciproque est cependant fausse, car le coefficient de corrélation indique uniquement une dépendance linéaire. D'autres phénomènes, par exemple, peuvent être corrélés de manière exponentielle, ou sous forme de puissance (voir série statistique à deux variables en mathématiques élémentaires).
Supposons que la variable aléatoire X soit uniformément distribuée sur l'intervalle [-1;1], et que Y = X2 ; alors Y est complètement déterminée par X, de sorte que X et Y ne sont pas indépendants, mais leur corrélation vaut 0.
Ces considérations sont illustrées par des exemples dans le domaine des statistiques.
 |
 |
 |
Relation de cause à effet

Une erreur courante est de croire qu'un coefficient de corrélation élevé induit une relation de causalité entre les deux phénomènes mesurés. En réalité, les deux phénomènes peuvent être corrélés à un même phénomène-source : une troisième variable non mesurée, et dont dépendent les deux autres. Le nombre de coups de soleil observés dans une station balnéaire, par exemple, peut être fortement corrélé au nombre de lunettes de soleil vendues ; mais aucun des deux phénomènes n'est probablement la cause de l'autre.
Exemple
En anthropométrie, on mesure pour un certain nombre d'individus
- la stature
- la hauteur du buste
- la longueur du membre supérieur
Plus ce nombre est grand et plus les corrélations sont représentatives. Puis on calcule par des lois statistiques l'influence des variables les unes sur les autres. On obtient la matrice suivante :
| Stature | Buste | Membre sup. | |
| Stature | 1 | ||
| Buste | 0,85 | 1 | |
| Membre sup | 0,55 | 0,63 | 1 |
- La valeur 1 signifie que les deux variables sont exactement corrélées, c'est le cas d'une relation exactement linéaire entre deux variables.
- Le 0,85 signifie que la stature joue pour 72,25 % (0,85) × (0,85) sur la valeur de la hauteur du buste, et ainsi de suite ...
- La moitié manquante de la matrice peut être complétée par une symétrie selon la diagonale si les corrélations sont réversibles.
Précautions à prendre
D'une manière générale, l'étude de la relation entre des variables, quelles qu'elles soient, doit s'accompagner de graphiques descriptifs, exhaustifs ou non dans l'appréhension des données à notre disposition, pour éviter de subir les limites purement techniques des calculs que nous utilisons. Néanmoins, dès qu'il s'agit de s'intéresser à des liaisons entre de nombreuses variables, les représentations graphiques peuvent ne plus être possibles ou être au mieux illisibles. Les calculs, comme ceux évoqués jusqu'à présent et donc limités par définition, nous aident alors à simplifier les interprétations que nous pouvons donner des liens entre nos variables, et c'est bien là leur intérêt principal. Il restera alors à vérifier que les principales hypothèses nécessaires à leur bonne lecture soient validées avant une quelconque interprétation.
Articles connexes
- Corrélation partielle (statistiques)
- Iconographie des corrélations
- Régression linéaire
- Corrélation de Spearman
- Tau de Kendall
- Corrélation d'images
- Corrélogramme
Notes et références
- ↑ Une vidéo de présentation du coefficient de corrélation est accessible ici.
- 1 2 3 4 Michel Armatte, « Le statut changeant de la corrélation en économétrie (1910-1944) », Revue économique, vol. 52, no 3, , p. 617-631 (lire en ligne)
- ↑ BOWLEY A.L. [1901], Elements of Statistics, Londres, King and Son, 2e éd. 1902,335 p.; 4e éd. 1920,454 p.; trad. française sur la 5e éd. par L. Suret et G. Lutfalla, 1929.
- ↑ YULE G.U. [1909], « Les applications de la méthode de corrélation aux statistiques sociales et économiques », BIIS, 28 (1), compte rendu de la 12e session de Paris, p. 265-277.
- ↑ FRECHET M. [1934], « Sur l’usage du soi-disant coefficient de corrélation », Rapport pour la 22e session de l’IIS à Londres, Bulletin de l’IIS.
- ↑ Les variables sont supposées appartenir à l'espace vectoriel
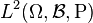 des variables aléatoires de carré intégrable.
des variables aléatoires de carré intégrable. - ↑ Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd ed.)
- Portail des probabilités et de la statistique
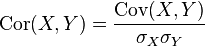
![\operatorname{Cor}(X,Y) = {\operatorname{E}[(X-\operatorname{E}(X))(Y-\operatorname{E}(Y))] \over \sigma_X\sigma_Y} = {\operatorname{E}(X Y) - \operatorname{E}(X) \operatorname{E}(Y) \over \sigma_X\sigma_Y}](../i/m/faf90c51053c5a590f52c125c210ae52.png)