Équation des télécommunications
L'équation des télécommunications, (appelée aussi équation de Friis par les Anglo-Saxons), permet d'obtenir un ordre de grandeur de la puissance radio collectée par un récepteur situé à une certaine distance d'un émetteur en espace libre. Il ne faut pas la confondre avec la formule de Friis, utilisée pour calculer le facteur de bruit d'un système.
Forme simple de l'équation
Dans sa forme la plus simple (cas idéal, pas de trajets multiples), l'équation de Friis s'exprime :
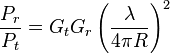
où :
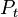 est la puissance en watts (W) délivrée à l'antenne d'émission (pertes d'adaptation et rendement non compris)
est la puissance en watts (W) délivrée à l'antenne d'émission (pertes d'adaptation et rendement non compris)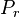 est la puissance en watts (W) collectée sur l'antenne de réception (pertes d'adaptation et rendement non compris)
est la puissance en watts (W) collectée sur l'antenne de réception (pertes d'adaptation et rendement non compris)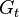 est le gain linéaire de l'antenne d'émission
est le gain linéaire de l'antenne d'émission est le gain linéaire de l'antenne de réception
est le gain linéaire de l'antenne de réception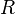 est la distance en mètres (m) séparant les deux antennes
est la distance en mètres (m) séparant les deux antennes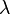 est la longueur d'onde en mètres (m) correspondant à la fréquence de travail
est la longueur d'onde en mètres (m) correspondant à la fréquence de travail
On suppose en outre que les antennes sont correctement alignées en termes de polarisation du champ. Toutes ces conditions ne sont jamais remplies dans une communication terrestre classique à cause d'obstacles, réflexions, trajets multiples, etc.
En communication spatiale, même si la propagation s'effectue principalement en espace libre, cette formule doit être corrigée également des atténuations atmosphériques et des éventuelles diffractions aux incidences faibles.
L'équation de Friis simple est donc à voir comme une borne « meilleur cas ».
Interprétation
Il est facile d'interpréter cette formule, en utilisant la relation entre le gain d'antenne et sa surface équivalente :

L'équation de Friis exprime alors simplement l'axiome de la propagation de l'onde électromagnétique sans pertes en espace vide :
Dans le cas d'un émetteur isotrope, l'énergie émise se répartit donc sur la surface d'une sphère de rayon R :
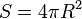
Une antenne de réception capte alors l'énergie dans le rapport de sa surface équivalente à cette surface totale :

Si on introduit une antenne d'émission non isotrope de gain Gt, la puissance précédente est simplement multipliée par ce gain :
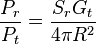
Cette interprétation élimine l'habitude courante de croire l'atténuation d'espace libre proportionnelle au carré de la fréquence. Ceci n'apparaît que dans la formule exprimée en gain d'antenne, et disparaît si on considère une antenne de réception de surface fixe. Au contraire, si on considère deux antennes de surface fixe, l'atténuation est proportionnelle au carré de la longueur d'onde.
Prise en compte des pertes d'antennes
Les antennes sont à l'origine de pertes par désadaptation et n'ont pas non plus un rendement idéal. L'équation précédente peut donc se compléter :
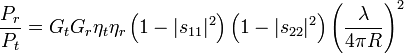
avec :
 est le coefficient d'efficacité de l'antenne d'émission
est le coefficient d'efficacité de l'antenne d'émission est le coefficient d'efficacité de l'antenne de réception
est le coefficient d'efficacité de l'antenne de réception est le coefficient de réflexion sur l'antenne d'émission
est le coefficient de réflexion sur l'antenne d'émission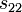 est le coefficient de réflexion sur l'antenne de réception
est le coefficient de réflexion sur l'antenne de réception
Prise en compte des pertes par désadaptation de polarisation
Les antennes d'émission et de réception ne fonctionnent pas forcément avec la même polarisation (par exemple, une polarisation circulaire à l'émission et une polarisation rectiligne à la réception). De plus, dans le cas où les deux polarisations sont rectilignes, il peut se trouver que les directions de polarisation ne soient pas alignées. On rajoute à la formule le terme 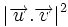 pour tenir compte de cette désadaptation. La formule complète devient alors :
pour tenir compte de cette désadaptation. La formule complète devient alors :

Expression logarithmique
Dans les calculs de bilan de liaison radioélectrique, l'équation de Friis est couramment remplacée par son expression logarithmique en décibels :
Puissance reçue (dBm) = Puissance transmise (dBm) + Gains des antennes (dB) - Pertes d'espace (dB) - Pertes diverses (dB)
Les décibels étant une unité logarithmique, ceci équivaut à un produit.

avec :
-
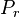 = Puissance reçue (dBm)
= Puissance reçue (dBm) -
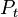 = Puissance transmise (dBm)
= Puissance transmise (dBm) -
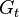 = Gain d'antenne émission (dBi)
= Gain d'antenne émission (dBi) -
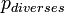 = pertes diverses (dB)
= pertes diverses (dB) -
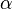 = perte de propagation (dB)
= perte de propagation (dB) -
 = Gain d'antenne réception (dBi)
= Gain d'antenne réception (dBi)
Le terme des pertes diverses peut se décomposer en pertes de lignes, pertes de désadaptations, de dépointage à l'émission et à la réception, de filtrage, de dépolarisation, etc. selon le détail du système étudié.
La perte de propagation peut s'exprimer de diverses façons, à partir de :
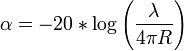 .
.
Soit en unités courantes :
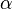 (dB) = 32,45 dB + 20*log [fréquence (MHz)] + 20*log [distance (km)][1]
(dB) = 32,45 dB + 20*log [fréquence (MHz)] + 20*log [distance (km)][1]
Prise en compte des trajets multiples
En espace libre, le terme d'affaiblissement s'exprime simplement 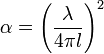 . Si l'onde se réfléchit sur
. Si l'onde se réfléchit sur 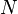 obstacles lors de sa propagation (murs, bâtiments, etc.), il faut alors écrire :
obstacles lors de sa propagation (murs, bâtiments, etc.), il faut alors écrire :

où :
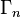 est le coefficient de réflexion sur l'obstacle
est le coefficient de réflexion sur l'obstacle 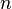
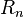 est la longueur du trajet
est la longueur du trajet 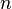
Notes et références
- ↑ people.deas.harvard.edu, Wireless Communication, « Radio Propagation Models »
Articles connexes
- Harald T. Friis
- Bilan de liaison
- Gain d'antenne
- Propagation des ondes radio
- Portail de l’électricité et de l’électronique
- Portail des télécommunications